2013年度　千葉県公立高校入試【後期】数学解説

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）７＋（－９）
＝７－９＝－２

（２）８÷（－２/３）²
＝８÷４/９＝１８

（３）３（２ａ－ｂ）－（ａ－３ｂ）
＝６ａ－３ｂ－ａ＋３ｂ　　←符号注意
＝５ａ

（４）正十角形の１つの内角を求める問題。
正ｎ角形の内角の和の式→１８０（ｎ－２）
１８０×（１０－２）＝１８０×８＝１４４０
よって、１４４０÷１０＝１４４°

（５）（√５＋√３）（２√５－√３）
＝１０－√１５＋２√１５－３
＝７＋√１５

（６）ｘ²－３ｘ－１　←因数分解できないので解の公式
＝（３±√９＋４）/２
＝（３±√１３）/２
計３０点

大問２（小問集合）

（１）
ｘ＝３のとき、ｙ＝１/３×３²＝３
ｘ＝６のとき、ｙ＝１/３×６²＝１２
変化の割合＝(ｙの増加量)/(xの増加量)
（１２－３） / (６－３)＝３　　よって、ウ

＠別解＠
ｙ＝ａｘ²のグラフにおいて、ｘの値がｐからｑまで増加するときの変化の割合はａ（ｐ＋ｑ）
１/３(３＋６)＝３

（２）
連立方程式。
ケーキの個数をｘ個、シュークリームの個数をｙ個をおく。
２５０ｘ＋２００ｙ＝４４００・・・【１】
また、個数の比から、ｘ：ｙ＝２：３
内項の積と外項の積が等しいから、３ｘ＝２ｙ　・・・【２】
【２】を変形、３ｘ－２ｙ＝０
【１】＋【２】×１００

　２５０ｘ＋２００ｙ＝４４００
＋)３００ｘ＋２００ｙ＝　　　０
　　５５０ｘ　　　　　＝４４００
ｘ＝８　　よって、ケーキは８個

（３）
円錐の体積＝底面積×高さ×１/３
底面積の円の半径は５ｃｍ。
高さは三平方の定理より、５：１２：１３ の直角三角形だから１２ｃｍ。
よって、５×５×π×１２×１/３＝１００πｃｍ³

（４）
確率＝（起こりえる場合の数）/（全体の場合の数）
全体・・６×６＝３６通り
起こりえる場合・・ａを基準に場合わけして調べる。
ａ＝１　　ｂ＝１、２、３、４、５、６
ａ＝２　　ｂ＝２、４、６
ａ＝３　　ｂ＝３、６
ａ＝４　　ｂ＝４
ａ＝５　　ｂ＝５
ａ＝６　　ｂ＝６　　　起こりえる場合の数は１４通り。
したがって、確率は１４/３６＝７/１８

（５）
「開いた角度」が９０°→垂線の作図

半直線ＢＡ。Aから等しい距離をとる。

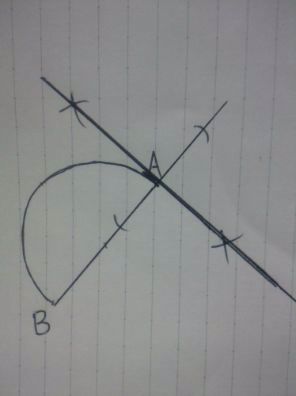
両端からヒョコヒョコ。
この線上に辺AB’がくる。

右側に半円を描きたい。
しかし、右側の半円の中心がわかっていない。
そこで、まず左側の半円の中心を探し、それを右側に移動させる。

直径ABの垂直二等分線と交わったところが点Ｏ
これが左側の半円の中心となる。

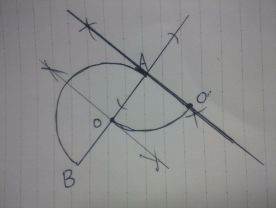
点Ａから点Ｏをとって、さきほどの線上と重ねる。
交点は点Ｏ’となり、右側の半円の中心となる。

最後にＡＯ’をとり、グルッと半周。
Ｂ’が求まる。

＠別解＠
Ａを通るＡＢとの垂線を描いたあと、Ｂを先に右側へ移動させ、
ＡＢ’の垂直二等分線からＯ’を求めて半円を作ることもできる。

大問３（文字式）

規則
【１】Ｐの値は、Ａに入れた数とＢに入れた数の和をなる。
【２】Ｑの値は、Ｂに入れた数からＣに入れた数をひいた値となる。
【３】Ｒの値は、Ａに入れた数とＣに入れた数の積となる。
【４】Ｓの値は、Ｐ、Ｑ、Ｒに表示された３つの数の和となる。

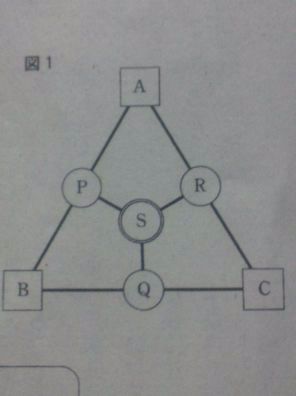
（１）文字式。
面倒くさそうにみえるが、式に置き換えてしまうと意外と単純に見えてくる。
Ｐ＋Ｑ＋Ｒ＝Ｓ
（Ａ＋Ｂ）＋（Ｂ－Ｃ）＋ＡＣ＝Ｓ
Ａに４、Ｂに１/２、Ｃにａ、Ｓに－１をそれぞれ代入する。
（４＋１/２）＋（１/２－ａ）＋４ａ＝－１
５＋３ａ＝－１
ａ＝－２

（２） 連続する３つの整数をｘ、ｘ＋１、ｘ＋２とおく。
同様に、Ａにｘ、Ｂにｘ＋１、Ｃにｘ＋２、Ｓに０を代入、因数分解。
｛ｘ＋（ｘ＋１）｝＋｛（ｘ＋１）－（ｘ＋２）｝＋｛ｘ（ｘ＋２）｝
＝（２ｘ＋１）＋（－１）＋（ｘ²＋２ｘ）
＝ｘ²＋４ｘ＝ｘ（ｘ＋４）＝０
ｘ＝－４、０　　よって、ａ＝－４、０

（３）代入までは前問と同様。式をうまく整列させるセンスが求められる。
（ａ＋ｂ）＋（ｂ－ｃ）＋ａｃ＝Ｓ
（ａ＋ｃ）＋（ｃ－ｂ）＋ａｂ＝Ｓ
結果は共にＳなので等式にする。
（ａ＋ｂ）＋（ｂ－ｃ）＋ａｃ＝（ａ＋ｃ）＋（ｃ－ｂ）＋ａｂ
ａ＋２ｂ－ｃ＋ａｃ＝ａ＋２ｃ－ｂ＋ａｂ
２ｂ－ｃ＋ａｃ＝２ｃ－ｂ＋ａｂ　　←ａを消去
３ｂ＋ａｃ－３ｃ－ａｂ＝０　　　　←すべてを左辺へ
３（ｂ－ｃ）－ａ（ｂ－ｃ）＝０　　←（ｂ－ｃ）で割る
３－ａ＝０
ａ＝３

＠別解＠
ｂ（３－ａ）－ｃ（３－ａ）＝０にしてもＯＫ。
この等式が成り立つためには、aが３でなければ成り立ちません。
ｂとｃがともに０であればａはなんでもよいのですが、
仮定からｂとｃは互いに異なる数となっています。
ｂが０でｃがＯ以外、ｃが０でｂが０以外を試してみましょう。
ａに３を入れなければ０にはできません。
すなわち、ａは必ず３でなくてはなりません。
ａ＝３

大問４（関数）

（１）関数ｙ＝６/ｘから、Ａ（２、３）Ｂ（－２、－３）

ＡとＢは原点に対象の点。
長方形の周は、４＋４＋６＋６＝２０ｃｍ

（２）最小の長さを考える前に、 わかるところから地道にひも解いていく。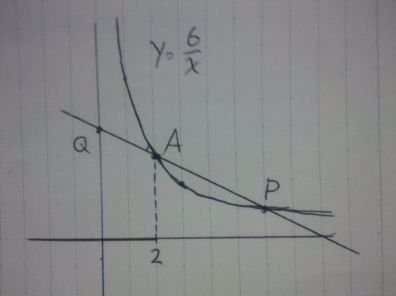
初期状態。

AP＝２AQから、ＱＡ：ＡＰ＝１：２　Ｐ座標が求まる。

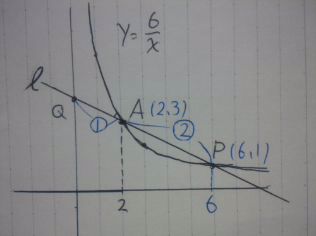
ＡとＰの座標が求まったので、直線ℓの式が求まる。
連立などで、ℓ：ｙ＝－１/２ａ＋４
切片Ｑの座標が（０、４）とわかる。

ここで、Ｒの位置を知りたい。
△ＰＱＲの周の長さが最小となるためにはＲをどこに置くべきか。
１辺であるＱＰはすでに長さが固定されているので、ＱＲ＋ＲＰの長さが最小になればよい。長さが最小＝直線！　直線を描くために、線対称を用いて１本の線に置き換える。
そこで、ｘ軸を対象の軸としてＱを対象移動させる。
Ｑ’（０、－４）とＰを結び、ｘ軸との交点がＲとなる。
（直線だからＱ’Ｐは最小の長さとなり、線対称よりＱＲ＝Ｑ’ＲなのでＱＲ＋ＲＱは最小となる）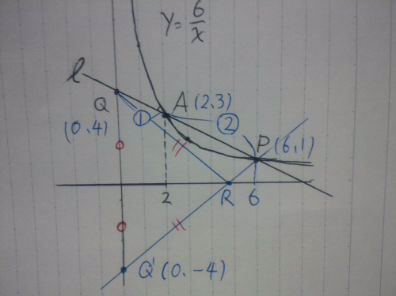
Ｑ’Ｐの直線の式を求める。
ｙ＝５/６ｘ－４
Ｒはｘ軸上の点なので、ｙ＝０を代入。
５/６ｘ－４＝０
５/６x＝４
ｘ＝２４/５
Ｒ（２４/５、０）

大問５（平面図形）

（１）誘導に従って解く。
△ＡＢＤと△ＢＣＥにおいて、対応する辺や角度を調べればよい。
正三角形の１辺より、ＡＢ＝ＢＣ・・（a）
正三角形の１角より、∠ＡＢＤ＝∠ＢＣＥ・・（ｂ）
仮定から、BD＝CE
以上より、合同条件は２辺とその間の角が等しい。・・（ｃ）
（ａ）・・・イ　（ｂ）・・・カ　（ｃ）・・・イ

（２）
「ＡＧを結ぶ」からＡＧを１辺とする三角形と、「ＢＦ＝ＣＧ」の証明から、
これらを１辺とする三角形のなかで合同っぽいものに目星をつけて検証する。
すると、△ＡＢＦと△ＡＣＧが合同っぽい。

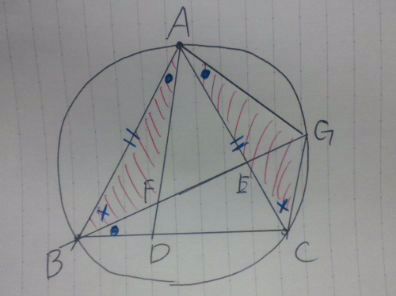
仮定から△ＡＢＣは正三角形　　ＡＢ＝ＡＣ
図形が円に囲まれている→円周角の定理をフル活用
弧ＡＧに対する円周角で、
∠ＡＢＦ＝∠ＡＣＧ＝×
前の証明から△ABD≡△BCEを利用。対応する角は等しいので、
∠ＢＡＦ＝∠ＣＢＥ＝●
さらに弧ＣＧに対する円周角で、
∠ＣＢＥ＝∠ＣＡＧ
つなげて、∠ＢＡＦ＝ＣＡＧ
一辺両端角が等しい→△ＡＢＦ≡△ＡＣＧ→対応する辺が等しい→ＢＦ＝ＣＧ

以下、模範解答例。
～～引用はじめ～～
△ABFと△ACGにおいて、
仮定から、AB＝AC　　　　・・・【５】
【４】より、∠BAF＝∠CBG　・・・【６】
弧CGに対する円周角が等しいことから、
∠CBD＝∠CAG　・・・【７】
【６】、【７】より、
∠BAF＝∠CAG　・・・【８】
弧AGに対する円周角が等しいことから、
∠ABF＝∠ACG　・・・【９】
【５】、【８】、【９】より、１辺とその両端角が等しいので、
△ABF≡△ACG
したがって、BF＝CG
～～引用おわり～～

（３）いわゆる、方べきの定理。
方べきの定理を知らなくても、中学で習う相似で乗り越えられる。
仮定と、前問で証明した合同な三角形をフルに使って長さを求める。

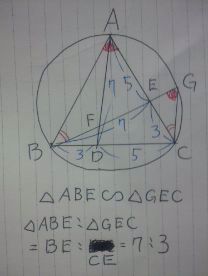
△ＡＢＥと△ＧＣＥにおいて、
弧ＢＣに対する円周角より、∠ＥＡＢ＝∠ＥＧＣ
弧ＡＧに対する円周角より、∠ＡＢＥ＝∠ＧＣＥ
２角が等しいので、△ＡＢＥ∽△ＧＣＥ
△ＡＢＥ：△ＧＣＥ＝ＢＥ：ＣＥ＝７：３
ＥＧ＝ＥＡ×３/７＝５×３/７＝１５/７
ＢＧ＝７＋１５/７＝６４/７ｃｍ
*方べきの定理・・ＢＥ×ＥＧ＝ＡＥ×ＥＣ
公立高校入試解説ページに戻る