2019年度　北海道公立高校過去問【数学】解説

平均30.1点（60点満点；学校裁量問題選択者は39.3点）


問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　91.2％
７＋（－５）＝７－５＝２

②　77.8％
－４÷１/９＋８＝－３６＋８＝－２８

③　77.8％
√６×√２－√３＝２√３－√３＝√３

（２）　80.4％
４（２ａ＋ｂ）＋（ａ－２ｂ）
＝８ａ＋４ｂ＋ａ－２ｂ
＝９ａ＋２ｂ

（３）　61.5％
ｘ＝１のとき、ｙ＝３
ｘ＝４のとき、ｙ＝９
３≦ｙ≦９

（４）　60.4％
最頻値（モード）→最も値の個数が多い。
２５回

（５）　64.8％
直角三角形なので、三平方の定理ａ²＋ｂ²＝ｃ²が成り立つ。
３：４：５からイ。
（√３）²＋（√７）²＝（√10）²で、オ。
イ・オ

（６）　80.2％
平行線と線分の比。

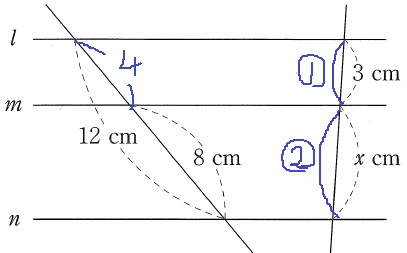
４：８＝１：２
ｘ＝３×２/１＝６ｃｍ

大問２（小問集合２）

（１）　63.9％
２ｘ²－18
＝２（ｘ²－９）
＝２（ｘ＋３）（ｘ－３）
*２ｘ（ｘ²－９）は１点とする。

（２）　61.5％
作図問題。
ＡＢ、ＢＣ、ＣＡのうち、２つを選び、
各々の直線の垂直ニ等分線が交わったところがＰとなる。

（３）　65.7％
全ての取り出し方は、４×３＝１２通り。
４の倍数となるには、１の位が４か８。
〔２個目のボール→１個目のボール〕と考えて、２×３＝６通り
６/１２＝１/２

*一の位は２個目のボールだが、そのときに４つのうち２つ（４か８）を選べば、
１個目のボールである十の位は何でもいい。
したがって、１/２と判断できる。

（４）　79.9％
２×２×π×□＝24π
□＝６ｃｍ

大問３（魔方陣）

（１）　36.7％

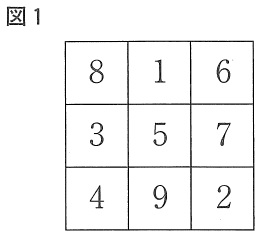
確かに、１列の和１５は中央のマス５の３倍にあたる。
説明の手順に従う。
１列の和をａとおく。

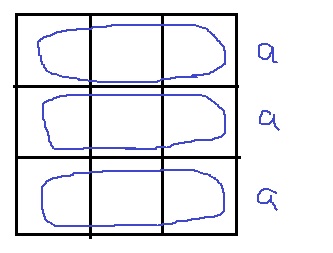
９マスの和は３ａ
ア…３ａ

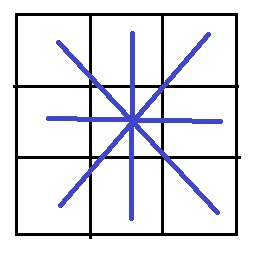
中央のマスは４列。
４列の和は４ａ。
イ…４ａ

今度は上の４列から、９マスの和を考える。
中央のマスをｂとおく。
４列の合計は、中央のマスを４回重複してカウントするので、３回分は余計となる。
９マスの和＝４ａ－３ｂ
ウ…３ｂ

３ａ＝４ａ－３ｂ
ａ＝３ｂとなるので、
１列の和ａは、中央のマスｂの３倍となる。

（２）　10.5％！
魔方陣。
方程式を使って説明する。

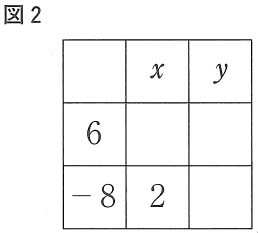
１列の和がわからない。
どこかでｘ、ｙを使って等式を作れないかを探す。

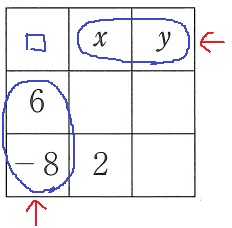
□＋ｘ＋ｙ＝□＋６＋（－８）
ｘ＋ｙ＝－２　…①

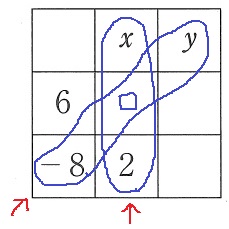
ｘ＋□＋２＝ｙ＋□＋（－８）
ｘ－ｙ＝－10　…②

ｘとｙの和と差がわかったので連立が組める。
①②を解いて、ｘ＝－６、ｙ＝４

大問４（関数）

（１）　65.8％
ｙ＝１/３ｘ²にｘ＝２を放り込む。
Ａ（２、４/３）
ＣはＡをｙ軸に対称移動した座標なので、（－２、４/３）

（２）　30.9％！
ｙ＝ｘ²にｘ＝６を代入。
Ｂ（６、３６）
ｙ＝１/３ｘ²にｘ＝２を代入。
Ａ（６、１２）
→Ｃ（－６、１２）
ＣからＢは、右に12、上に24なので、傾きは24/12＝２

（３）　22.3％！
ｔを使ったお馴染みのやり方。

ＡＢ＝ＡＣ
ＡＣ＝２ｔ
ＡＢ＝ｔ²－１/３ｔ²＝２/３ｔ²
２ｔ＝２/３ｔ²
２/３ｔ²ー２ｔ
＝２ｔ²－６ｔ
＝２ｔ（ｔ－３）＝０
ｔ＞０より、ｔ＝３

大問５（平面図形）

（１）　76.8％

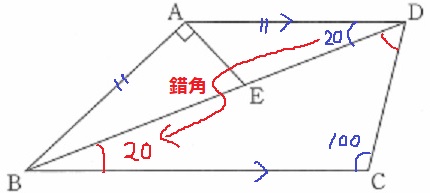
錯角で20°を下す。
△ＢＣＤの内角寄り、
∠ＢＤＣ＝180－（20＋100）＝60°

（２）　23.6％！
△ＡＢＦ≡△ＡＤＥの証明。

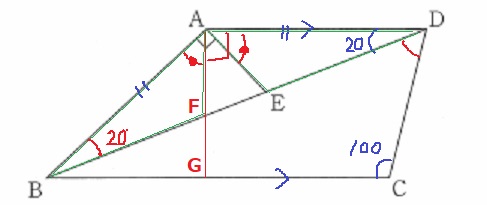
仮定から、ＡＢ＝ＡＤ
△ＡＢＤが二等辺だから、∠ＡＢＦ＝∠ＡＤＥ
２つの直角にはさまれた∠ＦＡＥを利用して、
∠ＢＡＦ＝∠ＤＡＥを整理して述べれば、一辺と両端角相等で合同。

学校裁量問題（大問５）

問１（１）　87.6％
△ＡＯＢは、５：１２：１３の直角三角形。
ＯＡ＝１３

（２）　24.7％！
図示。

△ＡＯＢと△ＡＣＤは２角が等しく相似。
ＡＣ＝３×１３/１２＝１３/４
１２－１３/４＝３５/４
Ｃ（５、３５/４）
ＯＣの傾きは、３５/４÷５＝７/ ４
ｙ＝７/４ｘ

問２
（１）　84.7％
クラスの人数24は度数。
クラス全員の（階級値）×（度数）＝720なので、
これを24で割ればクラス全員の階級値、すなわち、平均値がでる。
720÷２４＝３０ｋｇ

（２）　67.2％
表を埋めてみる。

赤い枠が18、青い枠が530。
アをｘとおくと、イは18－ｘ。
25ｘ＋35（18－ｘ）＝530
10ｘ＝100
ｘ＝10
よって、ア＝１０、イ＝８

（３）　37.6％
ラストの説明問題。
平均値が30ｋｇから29ｋｇに下がったということは、１年生の握力は30ｋｇ未満となる。

30人の（階級値）×（度数）の合計は、30×29＝870
2・3年生との合計の差は、870－720＝150
１年生６人の（階級値）×（度数）が150である。
６人は同じ階級に属するから、１年生の階級値は、
150÷６＝25ｋｇ
したがって、１年生６人の握力が入った階級は、
20ｋｇ以上～30ｋｇ未満である。
公立高校入試解説ページに戻る