2015年度　千葉県公立高校入試【前期】数学解説

平均４６．９点
問題はコチラ→ＰＤＦファイル

大問１（計算）－81.6％

(１)　96.6％
(－７)－(－４)
＝－７＋４　　
＝－３

(２)　93.1％
(－４)²＋８÷(－２)
＝16－４
＝12

(３)　74.6％
１/２(３ａ－２ｂ)－(２ａ－ｂ)
＝３/２ａ－ｂ－２ａ ＋ｂ     ←ｂが消える。
＝－１/２ａ

(４)　65.0％
２ａ－３ｂ＝１を、ｂについて解く。→　｢ｂ＝～｣の形にする。
３ｂ＝２ａ－１　←－３ｂと１を移項して、左右反転
ｂ＝（２ａ－１）/３

(５)　84.4％
√32－２√18＋５√２
＝４√２－６√２＋５√２　←ルート２に揃える。
＝３√２

(６)　75.9％
ｘ²－２ｘ=３(ｘ－1)を解く。
ｘ²－２ｘ＝３ｘ－３
ｘ²-５ｘ+３=０　　←因数分解できないので、解の公式
ｘ＝(５±√13)/２

大問２（小問集合）－41.8％

（１）　77.4％
例年通りの記号問題。正解がわかれば、他は特に検討しなくてもＯＫ。
解説なので１個ずつ検証。
ア：レンジ（range；範囲）は０～５冊。×
イ：モードは一番多いものなので３冊。×
ウ：メジアンは真ん中の値。２０人の場合は10人目と11人目の平均値。
下から数えていくと、ありがたいことに10人目と11人目がともに３冊。○
エ・・(０×２＋１×３＋２×４＋３×７＋４×１＋５×３)÷２０＝２．５５冊。×

（２）　43.2％
√の中が平方数になれば、√が外れて整数となる。
ｎの最小値は３。(ルートの中が３×３＝９で平方数となるから)
〔３×平方数〕も整数となる。ｎ≦50に留意してｎの値を求める。
３×1²＝３
３×2²＝１２
３×3²＝２７
３×4²＝４８
ｎ＝３、１２、２７、４８なので４個

（３）　65.6％
底面が半径４ｃｍの円。
高さは３：４：５の直角三角形なので３ｃｍ
４×４×π×３×１/３＝１６πｃｍ3

（４）　21.1％！
ユニークな確率問題。初見は少し戸惑う・・。
Ｐは点Ａから反時計回り。Ｑは点Ｅから時計回り。
直線ＣＧと”ねじれの位置”にある直線と問われたら、通常はＡＤ・ＥＨ・ＡＢ・ＥＦが思い浮かぶが、
どの辺もＰの通り道か、Ｑの通り道なので、直線ＰＱにならない。
かといって無いわけでもなく、例えばＡＦのような正方形の対角線や、
ＢＨのように立方体の対角線でも直線ＣＧとの”ねじれ”が起きる。
直線ＣＧと同一の平面にこない直線を１個ずつ調べる。

＠Ｐが点Ａにある＠
ＰがＡにくるのは大４。
ＱがＦかＨのときにネジレ　→ＡＦは小３、ＡＨは小１or５がでたときなので３通り

＠Ｐが点Ｂにある＠
ＰがＢにくるのは大１か５の２通り。
ＱがＥかＨのときにネジレ　→ＢＥは小４、ＢＨは小１or５がでたとき。３×２＝６通り

＠Ｐが点Ｃにある＠
直線ＣＧと交わるので無し。

＠Ｐが点Ｄにある＠
ＰがＤにくるのは大３。
ＱがＥかＦのときにネジレ　→ＤＥが小４、ＤＦは小３がでたときなので２通り。

ネジレのパターンは、３＋６＋２＝１１通り
大小サイコロの目の出方は６×６＝３６通り
よって、確率は１１/３６。

（５）　1.9％!!
難しい。
毎度、千葉の作図は、まだやるかっ！というくらい問題作成者が新しいパターンを発掘してくるので、
一体誰がこんな問題を気合いれて作っているのか。感嘆を禁じえません。
前問のザワザワ感から、本問で意気消沈した方もいるのでは・・。

大きい正方形の一辺をａ、小さい正方形の一辺をｂとします。

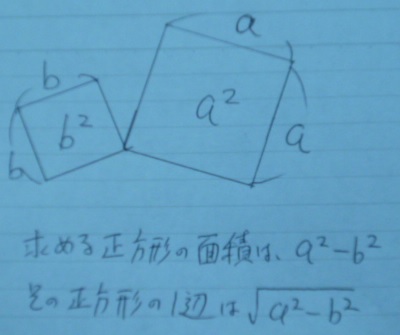
作図したい正方形の面積はａ²－ｂ²
その一辺は、根号をつける。
じゃあ、一体√(ａ²－ｂ²)という複雑な長さはどうしたら描けるのか？

ヒントは三平方の定理。

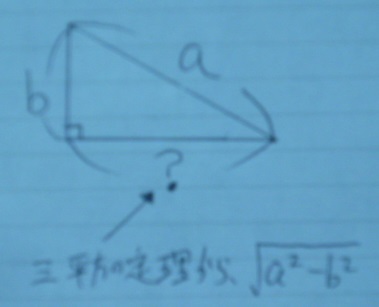
フォーカス機能がバカでボケてしまいました。
√(　)²-(　)² 　←この形は三平方の定理でお馴染みですよね。
よって、長い辺を斜辺とした直角三角形を想起。

じゃあこのような直角三角形はどうすればいいのか？

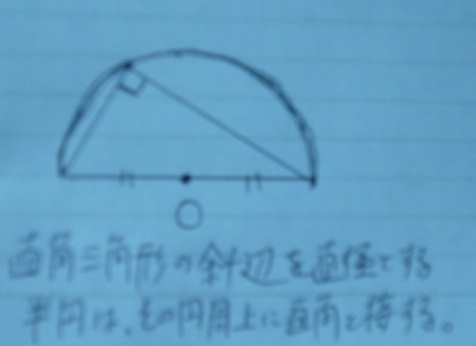
↑｢直角三角形の斜辺を直径とする半円は、その円周上に直角と接する｣と書かれてあります。

変な日本語ですみません。
ようは、斜辺の中点を中心にクルっと円を描くと、直角の部分が円周上にくるわけです。
これは受験生必須の知識として覚えておきましょう。
そして、直径に対する円周角は９０°で直角三角形になりますよね。まとめると…

①斜辺(=大きい正方形の１辺)の中心を発見(垂直二等分線の利用)
②中心から半円を描く(円周角の定理を利用するため)
③小さい正方形の１辺を、半円の端に接するようにもってくる。

こうすれば、”長い辺を斜辺とした直角三角形”を描けます。
三平方からの円周角という、２段階発想が辛い。

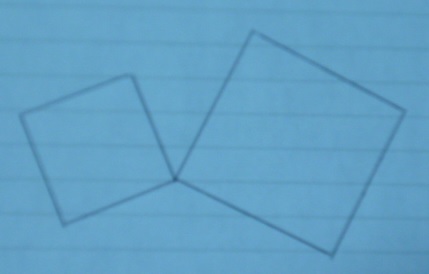
初期状態。

長い方の一辺を垂直二等分線。

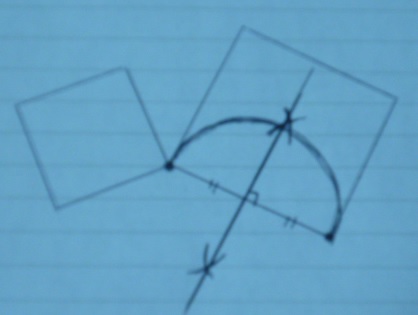
中心から半円をクル。

短い辺を回転移動。
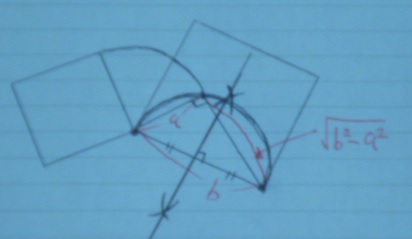
直角三角形の出来上がり。
カメラ撮ったあとにａとｂが逆になったことに気づく。。
求めたい正方形の１辺が現れる。

右の辺の長さをとって、ａ方向(左)に移す。
なぜか画像が赤く染まって病的に・・。

長さを維持したまま、２点からヒョコヒョコ。
４つの点が定まり、正方形が出来上がる。

＠別解＠

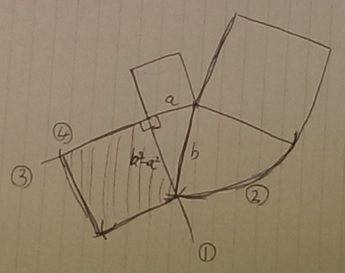
①小さい正方形の１辺を適当に延長
②大きい正方形の１辺を回転移動させて接着させる。
③④（ｂ²－ａ²）が作成できるので、これを１辺とする正方形を作成
これが最短ルートかな？

大問３（関数）－28.5％

（１）　68.6％
大問３は関数のグラフ。３つの線が交錯する。
複雑なグラフだが、ありがたいことに４つの交点のｘ座標が全てわかっている。
ＡＢＣＤどれからいってもＯＫ。

わかりやすいのはＤ座標かな？
Ｄ(４、８)なので、これをｙ＝ａｘ²に代入。
８＝16ａ　　ａ＝１/２

（２）【１】　16.6％！
直線ℓが追加。しかし、【１】は簡単。
ようはＥに直線ℓがきたとき、ＥがＱ、Ｅの真下とｙ＝ａｘ²との交点がＲとなる。

Ｅの交点は２直線の交点。
ｘ＋４＝－１/２ｘ＋３
ｘ＝－２/３
これをｙ＝ｘ＋４に代入して、ｙ＝１０/３
Ｅ(－２/３、１０/３)

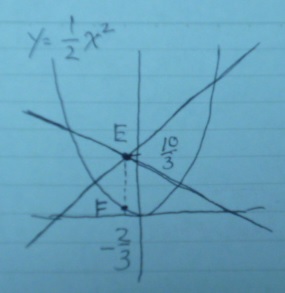
真下をＦとする。ＥＦの距離が答え。
Ｆのｙ座標は、ｙ＝１/２×(－２/３)²＝２/９
したがって、ＥＦ(問題文のＧＲ)は、１０/３－２/９＝２８/９cm

【２】　0.4％!!!
グラフが錯綜として、いろんなものがごちゃごちゃと混乱しやすい。
整理すると以下の感じ。

－３≦ｘ≦４ということは、点Ａ～点Ｄの間。
青の斜線の範囲内で、縦にスパンと割ったときに高さが３となるｘ座標が答え。

いびつな形だし、この際全ての点座標を求めてしまおう。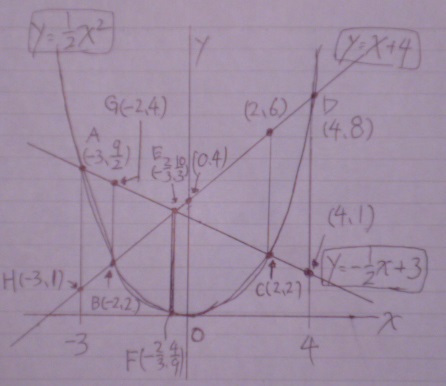 
変化するところに注意しながら求める。
数は多いが、多くは暗算で、しかも整数値になる。

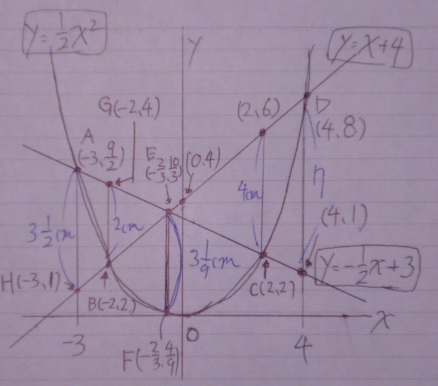
青い数字をみると、直線ℓがＤのときの高さは７ｃｍ、Ｃで狭まるが４ｃｍ、原点も４ｃｍ。
Ｅは前問から３と１/９ｃｍ。どれも３cmを超えている。
しかし、Ｂで２ｃｍと狭まり、Ａで３と１/２ｃｍ。
ということは、Ａ～Ｂ間、Ｂ～Ｅ間が怪しい。

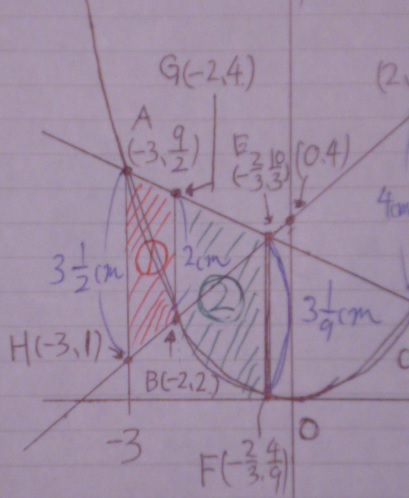
余分なところをカット。
ｘ座標でいえば、Ａ：－３≦ｘ＜－２と、Ｂ：－２≦ｘ＜－２/３。

Ａ：－３≦ｘ＜－２
高さが３となるｘ座標をｐをおく。
上がｙ＝－１/２ｘ＋３で、下がｙ＝ｘ＋４。この差が３となれば良いから、
－１/２ｐ＋３－(ｐ＋４)＝３
ｐ＝－８/３

Ｂ：－２≦ｘ＜－２/３
同様に、高さ３のときのｘ座標をｑとおく。
上がｙ＝－１/２ｘ＋３で、下がｙ＝１/２ｘ²。この差が３。
－１/２ｑ＋３－１/２ｑ²＝３　←３を消去。両辺に－１/２をかける。
ｑ²＋ｑ＝０
ｑ(ｑ＋1)＝０
ｑ＝－１、０
－２≦ｑ＜－２/３だから、ｑ＝－１

よって、答えは－８/３と－１。
細かい認定に骨が折れる。
問題文を整理したら、求めることができる点座標を片っ端から求める。ペンを走らす。
ターゲットを絞って、グラフの左側に全神経を集中させて計算。

＠別解＠

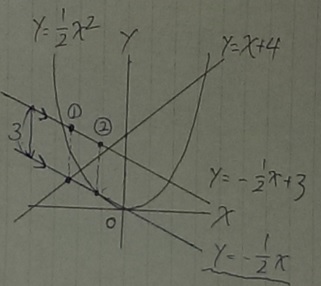
ｙ＝－１/２ｘ＋３を、ｙ軸方向に－３平行移動。すると原点を通る。
ｙ＝－１/２ｘ＋３とｙ＝－１/２ｘの距離は、ちょうど３。
【１】ｙ＝－１/２ｘとｙ＝ｘ+４
【２】ｙ＝－１/２ｘとｙ＝－１/２ｘ²の交点座標を求めて終了。
上のやり方は何だったのか思えるくらい、おそらくこれが最速のルート。

大問４（平面図形）－45.0％

(１)とりあえず誘導に従う。
△ＣＦＢと△ＡＣＢを凝視。これらの２角が等しくて相似らしい。
その２角がどこの角度であるのかを見極める。
本来、選択肢でなくても構わない問題に選択肢を用意してくれているので簡単。

(ａ)　87.9％
共通角だから∠Ｂのこと。(この時点でエ確定だが)
これを∠ＣＢＥに対応するようにいえば∠ＡＢＣ。エ。
(ｂ)　87.5％
円周角定理。直径に対する円周角は直角。∠ＡＣＢ。イ。
これらはサービス問題。

(ｃ)　６点―1.9％！　３点―0.9％　無答―72.2％！！
証明の続きを書く。

相似を利用するらしいので、対応する角に×を入れてみる。
線分ＣＥが∠ＡＣＦを二等分することの証明→∠ＥＣＡ＝∠ＥＣＦの証明
等しいこと前提に○をつけてみる。

↑（ボケてすみません・・）
ここで、ＢＣ＝ＢＥで△ＢＣＥが二等辺三角形であることに気づけば、さらに記入。
つまり、○×は二等辺三角形の底角→∠ＣＥＢ＝○×
そして、∠ＣＥＢを△ＡＣＥにおいて外角定理を利用。○と×が別れてくれる。
すると∠ＥＣＡ＝○＝∠ＥＣＦとなる。

以下、公表された模範解答。
～引用はじめ～
③より、∠ＢＣＦ＝∠ＢＡＣ　・・・④
円の半径から、ＢＣ＝ＢＥ　・・・⑤
⑤より、△ＢＣＥは、ＢＣ＝ＢＥの二等辺三角形なので、
∠ＢＣＥ＝∠ＢＥＣ　　　　　・・・⑥
△ＣＡＥにおいて、１つの外角は、これととなり合わない２つの内角の和に等しいので、
∠ＢＥＣ＝∠ＣＡＥ＋∠ＡＣＥ
よって、∠ＡＣＥ＝∠ＢＥＣ－∠ＣＡＥ
＝∠ＢＥＣ－∠ＢＡＣ　・・・⑦
また、∠ＥＣＦ＝∠ＢＣＥ－∠ＢＣＦ　　・・・⑧
④、⑥、⑦、⑧より、∠ＡＣＥ＝∠ＥＣＦ
～引用おわり～

(２)　2.6％！
例年通りの難易度。最初の切り口が見つからないと迷子。
半径が１ｃｍなので、とりあえず記入。

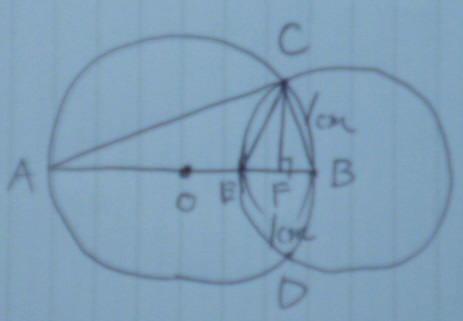
半径なのでＥＢも1ｃｍ。
ＣＥを求めたい。
△ＣＥＦは直角三角形→ＣＦとＥＦの長さがわかれば三平方の定理が使えるかも。

△ＣＦＢと△ＡＣＢの面積比が１：１６
わざわざ平方数を出してくるあたりから、辺の比が１：４であるのを利用すると察する。

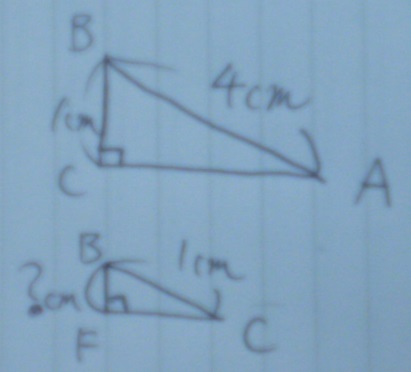
対応する辺に気をつけながら相似へ。
斜辺同士で、ＣＢ：ＡＢ＝１：４でＡＢが４ｃｍ。
ＡＢ：ＢＣ＝ＣＢ：ＢＦ＝４：１
よって、ＢＦ＝１/４ｃｍ

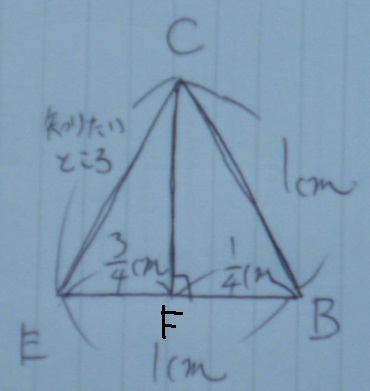
余分なところをカッティング。
ＥＦ＝１-１/４＝３/４ｃｍ
右の直角三角形で三平方→ＣＦの長さ→左の直角三角形で三平方。

ＣＢ²－ＦＢ²＝ＣＦ²＝ＣＥ²－ＦＥ²
１－１/１６＝ＣＥ²－９/１６
ＣＥ² ＝√３/√２＝√６/２
*何をしていいのかわからない場合は、わかるところをとりあえず書いてみる。
求めたいものから逆算する。

大問５（規則）－31.0％

昨年と同様、ラストは規則性。
格子点の数を求めるものだが、現場で実験しながら規則を発見する思考力を問われるので難しめ。
(１)(ア)　45.9％
図１を利用して、実際にｎ＝６のときの格子点の数を調べる。ＢＣ上にある点は３個。

(イ)　38.4％
図１の横が８マス用意されているので、１個ずつ調べてみる。
ＢＣ上の点は、２個、３個、５個いずれかで３通り。

(ウ)　50.0％
上の写真から５個。

(エ)　43.4％
図１を利用して数えてもＯＫ。
ただ、ここらへんで規則性を発見したい。
はるかが前半で述べているように、基本は長方形の半分の個数であるが、
ＢＣ上の点は隣の三角形と隣接するので、格子点の個数が重複する。
つまり、Ｎ＝(長方形の格子点+ＢＣ上の格子点の数)÷２
ただし、長方形の格子点は(ｎ+１）×(４+１)に気をつける！
３ｃｍの辺に格子点は両端にもあるので４個となる。
これらに気づけるか否かが成否の境目。
ｎ＝８はＢＣ上に５個の点があるから、
{(８+１)×(４+１)＋５}÷２＝５０÷２＝２５個

試しに、(ｎ＝１、Ｎ＝６)(ｎ＝２、Ｎ＝９)(ｎ＝３、Ｎ＝１１)(ｎ＝４、Ｎ＝１５)
(ｎ＝５、Ｎ＝１６)(ｎ＝６、Ｎ＝１９)をＢＣ上の格子点の数に注意しながら試してみよう。
規則通りになるはず。

(２)　6.0％！
先ほどの規則さえ発見できれば楽。最も多くなる場合は、ＢＣ上の格子点の数が５個のとき。
Ｎ＝{(ｎ＋１)(４＋１)＋５}÷２＝(５ｎ＋１０)/２

(３)　3.2％！！
最も少なくなる場合なので、ＢＣ上の格子点の数は２個。
Ｎ＝{(ｎ＋1)(４＋１)＋２}÷２＝(５ｎ＋７)/２＝１８６
ｎ＝７３
公立高校入試解説ページに戻る