平均52.3点(前年比;+0.5点)

問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1) 98.6%
6÷(-3)
=-2
(2) 92.4%
(3x-2y)-(x-5y)
=3x-2y-x+5y
=2x+3y
(3) 98.3%
√8+√18
=2√2+3√2
=5√2
(4) 92.4%
3x+y=4 …①
x-2y=13 …②
①×2+②
6x+2y=8
+) x-2y=13
7x =21
x=3
①に代入。9+y=4
y=-5
x=3、y=-5
(5) 86.2%
x2+3x-2=0
解の公式を適用。
x=(-3±√17)/2
(6) 85.1%
xとyの積が-16(y=-16/x)
y=-16÷4=-4
(7) 62.3%
3個の玉から2個の赤玉を取り出す確率→2/3
これをもう一度行うので、2/3×2/3=4/9
(8) 83.3%
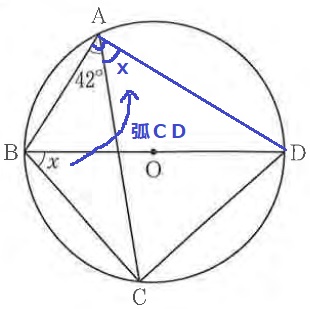
ADに補助線。
弧CDに対する円周角で、∠CAD=x
半円の弧に対する円周角は直角→∠BAD=90°
x=90-42=48°
大問2(数量変化)
(1) 57.2%
1L=1000cm3
12000cm3×75分÷(100cm×100cm)=90cm
(2)① 37.4%
満水までの時間は、おもりYなしで75分、おもりYありで55分。
ということは、おもりYの体積は12000cm3×20分に相当する。
これを面AEFBを底面積として割れば、高さFGがでる。
12000cm3×20分÷(60cm×80cm)=50cm
② 37.1%
おもりYの高さまで水が満たされる時間を求める。
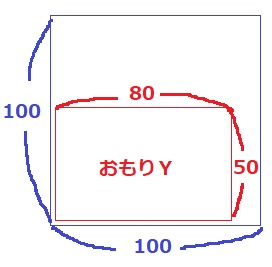
↑上からみた図。
(おもりYを除いた底面積×高さ60cm)の体積を1分あたり12000cm3で埋めていく。
(100×100-80×50)×60÷12000=30分
③符号…49.0%、時間…8.2%!!
おもりYの体積は50×80×60で、どの辺も20cmを超す。
最も早く水面を20cmにするには、最も面積の広い60×80=4800cm2を底面積にする。
→イ(面AEFB)
水の体積を12000cm3で割れば時間がでる。
(100×100-4800)cm2×20cm÷12000cm3
=8と2/3分=8分40秒
大問3(平面図形)
(1)ⅰ…84.3%、ⅱ…85.1%
△GDE≡△CDFの証明。
わかりにくい角度の証明はすでに明記されているのでありがたい。
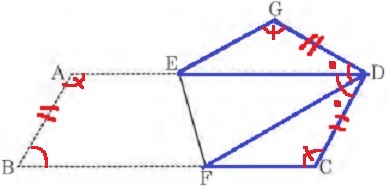
折り返しなので、折り返し前の平行四辺形に等辺と等角の印をつけるとわかりやすい。
1つ目は対辺+折り返し。
2つ目は対角+折り返し。
3つ目は対角+折り返し+間の∠EDFを控除。
1辺と両端角が等しいので合同となる。
ⅰ…イ、ⅱ…カ
(2) 66.1%
仮定より、∠GDC=90°
等角に印をつけよう。

△CDFは二等辺で、その底角から錯角につなげる。
先ほどの合同から、対応する角に印をつける。
すると、∠GDCに3つの●が集まる。
∠EDF=90÷3=30°
(3) 26.8%!
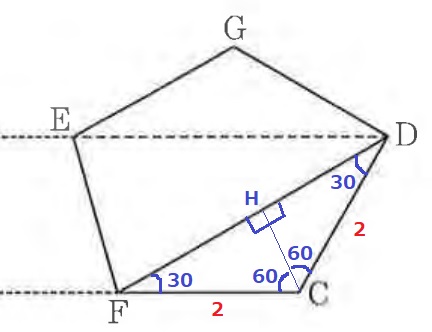
△CDFの内角は30°-30°-120°
CからDF方向にむけて垂線、DFとの交点をHとすると、
CHは二等辺三角形CDFを2等分し、30°-60°-90°の直角三角形が2つできる。
辺の比は1:2:√3だから、DF=2×√3/2×2=2√3cm
(4) 6.2%!!
前図より、HC=2×1/2=1cm
△CDF=2√3×2÷2=√3cm2
△GDEも合同で√3cm2
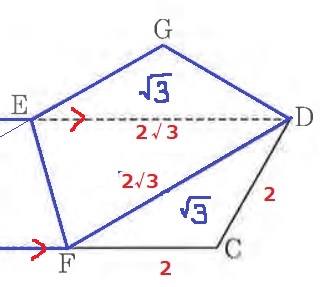
上底と下底の比から、△CDF:△DEF=FC:ED=2:2√3
△DEFの面積は、√3×2√3/2=3cm2
五角形CDGEFの面積…3+√3×2=3+2√3cm2
大問4(データの活用)
(1)最頻値…81.6%、平均値…51.6%
最頻値(モード)…最もあわられている値。
階級値で答える。6.5と7.5の平均で7cm。
平均値
これも階級値で計算する。
(5×6+6×5+7×12+8×7+9×10+10×10)÷50
=390÷50=7.8cm
(2) 47.0%
条件に合わないものを外していく。
①最頻値がAと同じく7cm。
→イが外れる。
②50個の中央値(メジアン)は25番目と26番目の平均。
Aの中央値は8cm。
30個のメジアンは15番目と16番目の平均値で、これが8cmとなるものを探す。
→ア・ウ・カが外れる。
③Aにおける階級値6cmの相対度数は、5/50=0.1
Bにおける階級値6cmの度数は、30×0.1=3個となる。
→オが外れてエ
(3)Ⅰ 27.8%!
6.5cm以上より6.5cm未満の方が計算が少ない。
Aの6.5cm未満の相対度数は、11/50
Bの6.5cm未満の相対度数は、6/30=1/5
6.5cm以上の相対度数は、
A…39/50=78/100=0.78
B…4/5=0.8
6.5cm以上の割合が大きいのはB。
Ⅱ
Bのタマネギは全体で300個なので、
300×0.8=240個
*タマネギ生産量3位は兵庫。
いわゆる近郊農業で、淡路島のタマネギは有名ですね。
大問5(関数)
(1) 84.3%
放物線では、傾きaの値が小さいほどグラフは広がっていく。
ウ
(2) 71.3%
y=1/2x2のx>0、y>0(第一象限)において、
xとyの値が等しくなるAのx座標aを求める。
a=1/2a2
1/2a2-a
=a(1/2a-1)=0
a>0より、a=2
*勘のいい人は2を代入すれば(2,2)になると直感で解けてしまう。
(3)① 41.4%
グラフの式から座標を確定する。

何度回転させたかは問題文に書かれていないが、なんとなく90°の予感はする。
ODとEDを結ぶ。Dから垂線をおろし、x軸との交点をFとする。
ODの傾きは1なので∠DOF=45°
これを手がかりに角度を調べていくと、△OABも△ODFも直角二等辺三角形。
△ODFが△EDF’に回転移動するので、回転角度である∠ODE=90°
∠EDF’=45°(EDの傾き-1)
D(4、4)から左に4、上に4いくとE(0、8)
② 1.1%!!

うえのように移植すると求積すべき図形は、
大きい4分の1円-小さい4分の1円+直角二等辺三角形。
直角二等辺三角形の面積は△OABと合同で4×2÷2=4cm2
問題は大きい4分の1円の半径。
扇形の弧上にあるBをヒントに、△BCDの三平方でBDを求める。
半径BD=√(62+22)=√40cm
△ACDで三平方、半径AD=√8cm
よって、√40×√40×π×1/4-√8×√8×π×1/4+4
=8π+4cm2
大問6(規則)
(1)① 78.8%
本問は数字が3種類しかなく、ルートもわかりやすいので数字が交互に並ぶだけが、
サイコロが複雑なルートをたどる場合は、うえのように側面も書いて調べていくと確実。
サイコロが直線で移動するときは、横の面は常に同じである。
② 37.1%
前問では、a=3、b=7であった。
aは2マス、bは4マス。
a+b=10、a<bの条件で、2a+4bの値が最も小さくなるaとbの組み合わせを考える。
bの値を最小にすればいい。
→a=4、b=6
③ 2.6%!!
ここからグッときつくなる:;(∩´_`∩);:
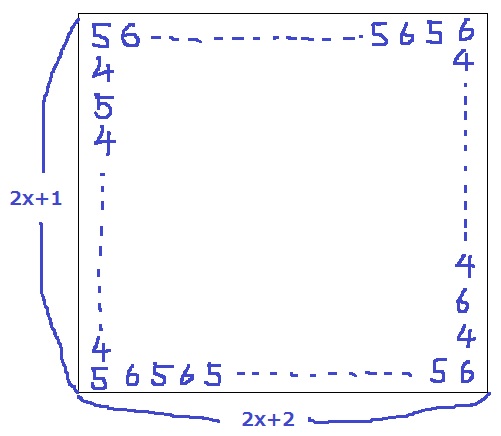
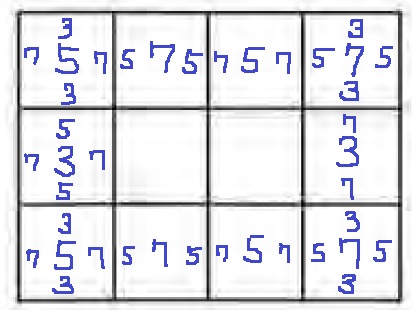
はじめは5で縦列は奇数だから、5454…5で終わる。
右に向かって5656…偶数だから6で終わる。
うえに6464…奇数で6で終わり、左に6565…1マス減って奇数だから6で終わる。
この合計が2020となる。

この後はいろいろなやり方があると思われる。
サボは上図のように分けました。
5454…が2x個あるので、5と4をワンセットで9にすれば、9がx個あることになる。
同様に、右の6464…は10がx個。
下の5656…5と上の6565…6は対称的な並びなので、
上下で2行を足せば、11が2x+1個あるのと同義である。
9x+10x+11(2x+1)=2020
41x=2009
x=49
(2) 0.5%!!!
きちぃ(´゚д゚`)
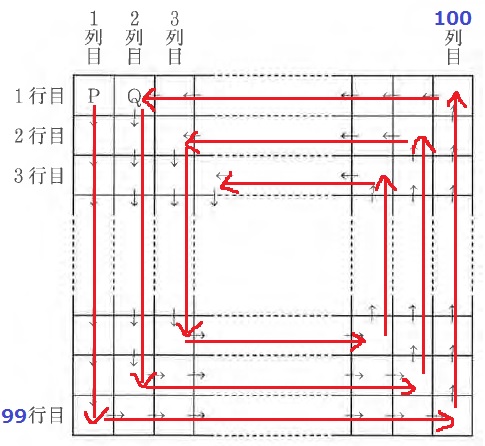
このように螺旋状でサイコロをころころ転がしていったときの最後の様子が知りたい…。
まずは場所を探る。

行も列も外側からなくしていく。
行は(1、99)(2、98)…と和が100となるセットで消していくと、50が最後に残る。
同様に列は(1、100)(2、99)…と和が101となるセットで消すと、最後が(50、51)。
縦方向の列は(左列→右列)の順で消えるので最後は51。
50行目51列目。
問題はそのときに記録された数。
全部でマスは99×100=9900マスあり、最初のPを除いて9899回サイコロを転がす。
ゴールが奇数回なので、奇数回を調べればよいのでは?

四隅だけを調べ、奇数回に〇をつけてみた。
すると、〇のなかの数字はカーブを曲がるごとに、
4→6→6→6→6→5→5→5→5→4→4→4→4…
はじめの4を除いたら6→5→4の順で4つずつの固まりが見つかる。

1列目だけを分離。
右側は99×99の正方形で、奇数回の外周が6→5→4…で繰り返される。
求めたい50行目51列目はこの正方形の真ん中にいる。
99の真ん中は”50行目”の50番目。
50÷3=16…2
余り2は6→5、真ん中の数字は5となる。
●講評●
大問1
全体的に正答率が良い。稼ぎポイント。
(7)確率×確率が考えやすい。
大問2
(2)③符号が合っていれば時間も出しすいと思うのだが。。
底面積×高さ=体積、体積÷1分あたりの水量=時間
大問3
(4)上底と下底の比から面積比を捉えるやり方は応用がきく。
他の都道府県でも頻出なので押さえておく。
大問4
(2)処理手順が多いが、半数の生徒が正解〇
(3)数の少ない6.5未満が数えやすい。
大問5
(3)②移植で求積すべき形がわかっても、半径が出しずらい。
扇形の弧のうえにある点に見当をつけ、三平方で攻略する。
大問6
(1)③和が2020なので自力では無理。
効率の良い処理で時間のロスを食い止めたい。
(2)シビアであった。
さっさと諦めて他を確実にとりにいった方が良い。
十数回のコーナーの判定で、一応規則は見つけられる。
数学的な手法ではなさそうだが(;`ω´)



コメント