2019年度　香川県公立高校過去問【数学】解説

平均27.2点（最高…50点、最低…０点）
問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）
４－３×（－１）
＝４＋３＝７

（２）
（３/４－２）÷５/６
＝－５/４×６/５＝－３/２

（３）
３ａ²ｂ×４ａｂ÷（－２ｂ）
＝－６ａ³ｂ

（４）
√12＋√３（√３－６）
＝２√３＋３－６√３
＝３－４√３

（５）
２ｘ²－20ｘ＋50　←両辺を２で割る
＝２（ｘ²－10ｘ＋25）
＝２（ｘ－５）²

（６）
（ｘー３）（ｘ＋４）＝－６
ｘ²＋ｘ－６＝（ｘ＋３）（ｘー２）＝０
ｘ＝－３、２

（６）
ａ＝10ｂ＋５

大問２（図形）

（１）

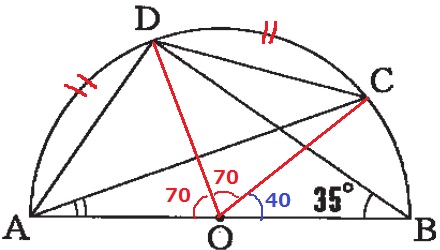
円周角の定理から、∠ＡＯＤ＝35×２＝70°
孤ＡＤ＝孤ＤＣなので、∠ＣＯＤ＝70°
∠ＢＯＣ＝180－70×２＝40°
∠ＢＡＣ＝40÷２＝20°

（２）ア
面ＥＦＧＨは直方体の底面。
これと垂直な線分は直方体の高さにあたる。ア
*ウ・エは面ＥＦＧＨと平行。

イ
△ＡＢＤは直角二等辺三角形。
１：１：√２から、ＡＢ＝ＡＤ＝√２ｃｍ
△ＡＢＦで三平方。ＢＦ＝√７ｃｍ
√２×√２×√７＝２√７ｃｍ³

（３）
出来そうで出来ないもどかしさ:;(∩´＿`∩);:

△ＥＢＣに着目すると、５ｃｍ：12ｃｍ：13ｃｍの直角三角形が見つかる。
○＋×＝90°と錯角を使い、角度を調査していく。
角度が○、×、90°となる三角形の辺の比はすべて５：12：13。

本問の決め手はＦＨ＝９ｃｍをうまく利用するものと思われる。
ＦＨを一辺とする直角三角形が欲しい。

ＤＡとＣＥを延長して、交点をＪとする。
△ＪＦＨの内角から５：12：13。
ＪＨ＝９×12/５＝108/５

△ＪＡＥも同様で５：12：13。
ＪＥ＝７×13/５＝91/５

ＥＨ＝108/５－91/５＝17/５
ＨＣ＝13－17/５＝48/５ｃｍ

＠余談＠

Ｈから４本の直線が90°ずつ四方に伸びているので、
４つのパーツを配置転換させたら正方形ができました。

もとの正方形の面積は12×12で、５×５の正方形が空洞となります。
ＥＣ（うえの図形では横の辺）が13ｃｍで、縦も13ｃｍ。
12²＋５²＝13²で三平方が成り立ちますね。
ＦＩ＝13ｃｍとなり、ＨＩ＝13－９＝４ｃｍ
△ＩＨＣで５：12：13より、ＨＣ＝４×12/５＝48/５ｃｍ

大問３（小問集合）

（１）
ｘ＝－２、ｙ＝１を放り込んで、等式が成り立つものを選ぶ。
イ・エ

（２）
カードの取り出し方は、４×５＝20通り
結果がＡ＞Ｂとなるパターンを調査。
Ａ２…Ｂ０・１
Ａ４…Ｂ０・１・３
Ａ６…Ｂ０・１・３・５
計９通り⇒９/20

（３）
7.0未満の度数の合計を求める。
Ａは12人、Ｂは８人。
Ｐ…12÷80＝0.15
Ｑ…８÷40＝0.2
*相対度数は分数ではなく、小数で求める。
Ａの方が相対度数が小さい→イ

（４）ア
ｘ＝０のとき、最小値ｙ＝０
ｘ＝３のとき、最大値ｙ＝９
０≦ｙ≦９

イ
解答欄では過程も記述する。

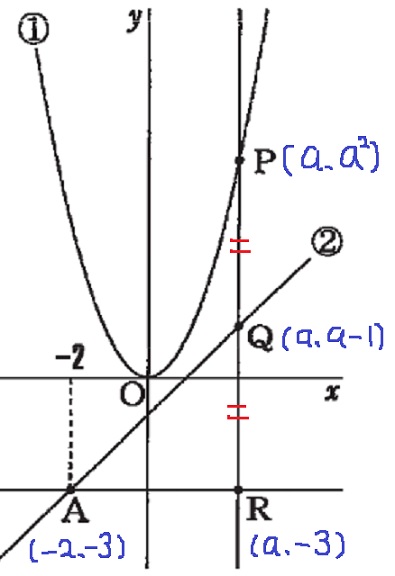
Ｐのｘ座標をａとして、Ｐ・Ｑ、Ｒの座標を求める。
Ｒのｙ座標はＡと同じ。
②：ｙ＝ｘ－１→Ａ（－２、－３）
Ｒ（ａ、－３）

ＰＱ＝ＱＲ
ａ²－（ａ－１）＝ａ－１－（－３）
ａ²－２ａ－１＝０
Ｐのｘ座標は正の数なので、ａ＞０より、ａ＝１＋√２

大問４（方程式）

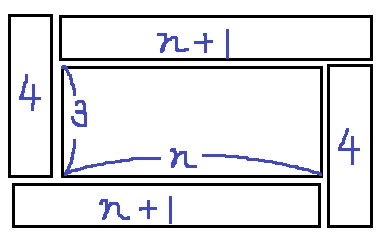
（１）ア

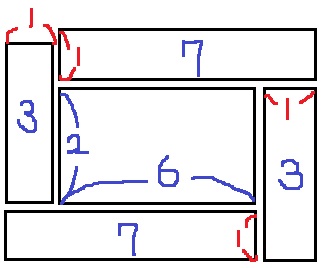
↑この形が見えれば一発かと。
（３＋７）×２＝20枚
20ｃｍ²

イ

３ｎ＝２{４＋（ｎ＋１）}
３ｎ＝２ｎ＋10
ｎ＝10

（２）ア
午前10時に５個追加され、Ａは３個検査して出荷するので、
２個増えている。

イ
下線部について、等式を完成させる。
【最初からあった製品＋新たに供給された製品＝検査した製品】
最初からあった製品･･･ｘ個
新たに供給された製品･･･５×21＝105個
１日あたり、ＡとＢは３個、Ｃはｙ個検査する。
１～７日目の検査…ＡＢＣの３人⇒７（６＋ｙ）個
８～21日目の検査（14日間）…ＢＣの２人⇒14（３＋ｙ）個

ｘ＋105＝７（６＋ｙ）＋14（３＋ｙ）
ｘ＝21ｙ－21

ウ
過程も記述する。
立式の方法は前問と同様。
11日間のうち、最初の３日間はＡＢＣ、後半の８日間はＢＣＤで行う。
Ｄは１日あたり、Ｃと同じｙ個の製品を検査する。
ｘ＋５×11＝３（６＋ｙ）＋８（３＋２ｙ）
ｘ＝19ｙ－13

前問の答えと連立を組む。
21ｙ－21＝19ｙ－13
ｙ＝４
いずかの式に代入して、ｘ＝63
ｘ＝63、ｙ＝４

大問５（図形の証明）

（１）
△ＢＥＨ∽△ＢＡＤの証明

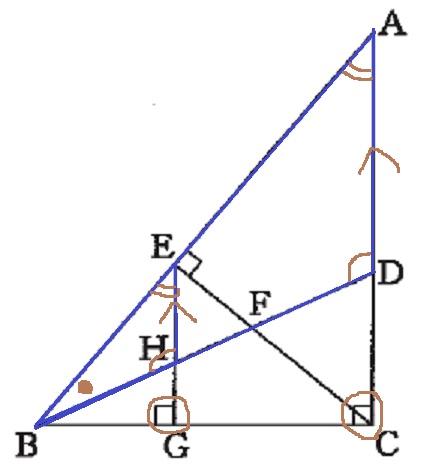
●が共通角。
∠ＢＧＥ＝∠ＢＣＡ＝90°
同位角が等しいので、ＥＧ//ＡＣ。
同位角で２角が等しい→∽

（２）
先に公式解答を引用（サボ解説はあとで書きます）

手順が長いので、流れを概括します。

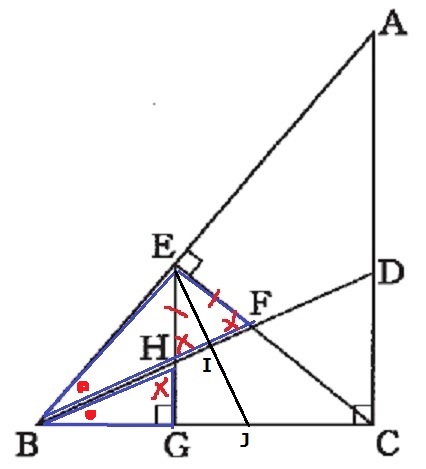
△ＢＨＧ∽△ＢＦＥ（直角と共通角●）
対応する角で∠ＢＨＧ＝∠ＢＦＥ
対頂角から∠ＢＨＧ＝∠ＥＨＦ
△ＥＨＦは二等辺になる⇒ＥＨ＝ＥＦ

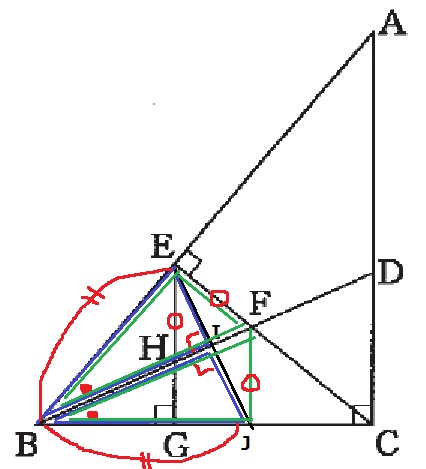
続いて、△ＢＥＩ≡ＢＪＩ（一辺両端角）
ＢＥ＝ＢＪ
さらに、△ＢＦＥ≡△ＢＦＪ（２辺と間の角）
ＥＦ＝ＦＪ

ＥＨ＝ＥＦ＝ＦＪとなり、ＥＨ＝ＦＪが導ける。

＠別解＠

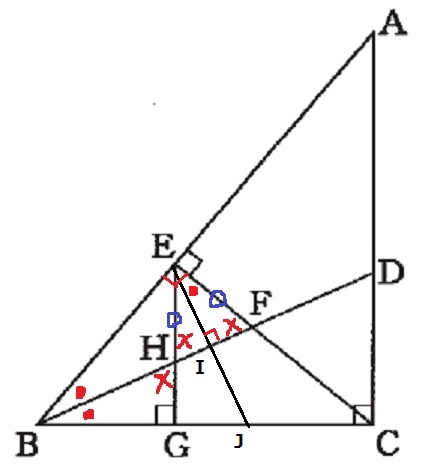
△ＢＧＨにおいて、∠ＨＧＢ＝●、∠ＢＨＧ＝×とする。
●＋×＝90°をもとに角度を調査していく。
△ＢＥＦで∠ＢＦＥ＝×
∠ＥＨＦは対頂角で×
△ＥＦＨは底角が等しいので二等辺三角形。
ＥＨ＝ＥＦ
△ＥＩＦで∠ＩＥＦ＝●

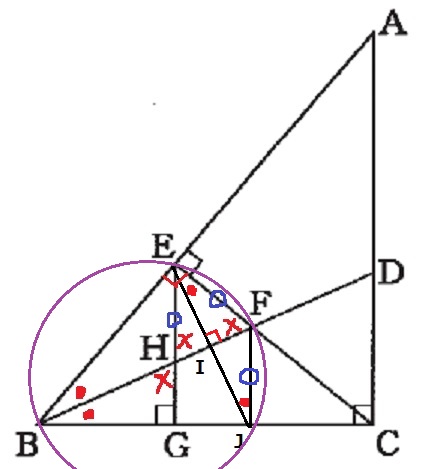
∠ＪＢＦ＝∠ＪＥＦに注目！
２点Ｂ、Ｅが直線ＪＦについて同じ側にあり、∠ＪＢＦ＝∠ＪＥＦが成り立つので、
円周角の定理の逆により、４点Ｂ・Ｅ・Ｆ・Ｊは同じ円周上にある。
四角形ＢＥＦＪが円に内接するので、円周角の定理から∠ＥＢＦ＝∠ＥＪＦ
△ＥＦＪは底角が等しいので二等辺三角形⇒ＥＦ＝ＦＪ
ＥＨ＝ＥＦ＝ＦＪより、ＥＨ＝ＦＪ

＊備考＊
△ＦＩＪで∠ＩＦＪ＝×、△ＦＢＪで∠ＦＪＢ＝90°
（もしくは、内接する四角形の対角の和が180°であるから、
∠ＦＪＢ＝180－∠ＦＥＢ＝90°）
∠ＥＧＢ＝∠ＦＪＢ＝90°から同位角が等しくなり、ＥＨ//ＦＪ
ＥＨ＝ＦＪなので、１組の対辺が等しくかつ平行→四角形ＥＨＪＦは平行四辺形。
加えて、対角線ＨＦとＥＪが直交するので、四角形ＥＨＪＦは菱形となる。

以下、公式からの概評。

公立高校入試解説ページに戻る