2018年度　神奈川県公立高校入試【数学】解説

平均５６．０点

問題はコチラ→ＰＤＦファイル

大問１（計算）

（ア）　98.2％
（－８）＋（－４）＝－８－４＝－１２

（イ）　98.4％
－５/７＋２/３＝－１/２１

（ウ）　97.9％
６５ａ²ｂ÷５ａ＝１３ａｂ

（エ）　96.4％
１８/√２－√９８　　←有理化
＝９√２－７√２＝２√２

（オ）　90.1％
（ｘ＋９）²－（ｘ－３）（ｘ－７）
＝ｘ²＋１８ｘ＋８１－ｘ²＋１０ｘ－２１
＝２８ｘ＋６０

大問２（小問集合）

（ア）　94.2％
（ｘ＋４）をラージエックスで置き換えるとラク。
（ｘ＋４）²－２（ｘ＋４）－２４
＝Ｘ²－２Ｘ－２４
＝（Ｘ＋４）（Ｘ－６）　　←ここでＸを（ｘ＋４）に戻す
＝（ｘ＋４＋４）（ｘ＋４－６）
＝（Ｘ＋８）（Ｘ－２）

（イ）　79.7％
解の公式。ｘの係数が偶数なので、ｂ＝２ｂ’バージョンが使えます。
ｘ＝（１±√７）/６

（ウ）　81.8％
ｙ＝ａｘ²のグラフにおいて、
ｐ→ｑまで増加するときの変化の割合はａ（ｐ＋ｑ）
ａ（２＋５）＝－４
７ａ＝－４　　a＝－４/７

（エ）不等式　93.4％
おつりを受け取ったということは、支払代金は１０００円より少ない。

（オ）　47.3％
ルートのなかが平方数になれば整数となる。
ｎは正の整数なので、（53－２ｎ）の値は５３より小さくなる。
√（53－２ｎ）＜√64（＝８）　→つまり、８未満の平方数が候補。
１～７の平方数を並べる。
５３－２ｎ＝１、４、９、１６、２５、３６、４９
５３は奇数。２ｎは偶数。
ｎが整数となるためには、〔奇数－偶数＝奇数〕より、
奇数の平方数である１、９、２５、４９が答えとなる。　→　４個

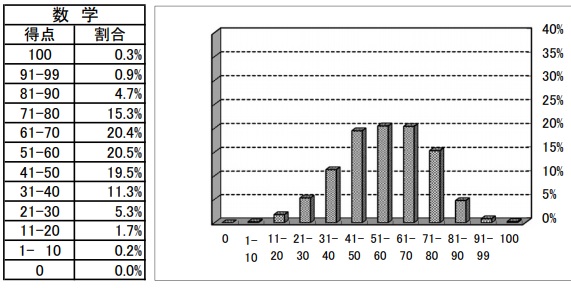
（カ）　57.3％
階級値は各階級の真ん中の値。
（１２×１＋１６×３＋２０×８＋２４×６＋２８×２）÷２０
＝４２０÷２０＝２１．０
大問１と合わせて３９点。ここらへんまでは安定してとりたい。

大問３（図形と文字式）

（ア）　2.8％！
平面図形。地味にムズイ(;´д｀)
相似を使うのはわかるが、変なところを求めさせられるのできつい。
とりあえず、長さがわかっているところに数字を書いてみよう。
EB＝１、BF＝２、FC＝１、CD＝２
ＥＦとＦＤに補助線をひいてみよう。
見慣れた図形が真ん中にできるはず。

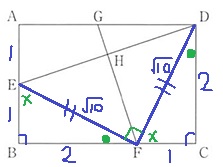
△EBFと△FCDは２辺と間の角で合同。
EF＝FD
●＋×＝９０°だから、∠EFD＝９０°となる。
すると、△EFDは直角二等辺三角形

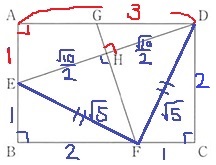
HFとEDは垂直に交わるので、HはEDの中点
△EFDの三平方からED＝√１０
HD＝√１０/２
　
△EDA∽△GDHから、
EA：AD＝GH：HD＝１：３
GH＝√１０/２×１/３＝√１０/６ｃｍ

（イ）文字式　　61.5％
情報さえ整理できれば攻略できる。
図を描くクセを身につけましょう。
時間で等式を立てる。

大問４（関数）

（ア）グラフの傾き　88.9％
ｙ＝ｘ＋６から、B（６、１２）
これをｙ＝ａｘ²に放り込む。
１２＝６²ａ
３６ａ＝１２
ａ＝１/３

（イ）ＥＦの式を求める。　36.2％
Ａ（－３、３）　Ｄ（０、－７）
ＥはＡＤの中点なので、Ｅ（－３/２、－２）
これとＦ（６、０）が通る式を求める。
ｙ＝ｍｘ＋ｎに代入して連立。
－２－３/２ｍ＋ｎ　・・①
－４＝－３ｎ＋２ｎ　・・①×２
０＝６ｍ＋ｎ　　　　 ・・②
０＝１２ｍ＋２ｎ　　・・②×２
以上から、ｍ＝４/１５
　
②に代入。　０＝６×４/１５＋ｎ
ｎ＝－８/５

（ウ）△ＡＧＢと△ＤＦＧの面積比 　2.8％!!

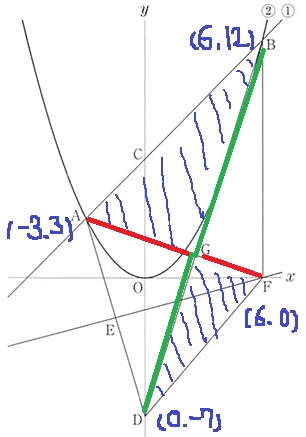
指針としては、赤×緑をすれば各々の面積比がでる。
２つの直線が交差するＧの座標が知りたい。
数字がキレイではなく、作業も多い（以下：結果だけ）。
ＤＢ：ｙ＝１９/６ｘ－７
ＡＦ：ｙ＝－１/３ｘ＋２
２つの直線の交点Ｇ（１８/７、８/７）

ＡＧ＝３＋１８/７＝３９/７
ＧＢ＝１２－８/７＝７６/７
ＤＧ＝７＋８/７＝５７/７
ＧＦ＝６－１８/７＝２４/７
ＡＧ×ＧＢ：ＤＧ×ＧＦ
＝３９×７６：５７×２４
＝１３：６
△ＡＧＢ：△ＤＦＧ＝１３：６

前問でキレイな数字ではない連立を解かせたのに、本問はそれを前提にしていない・・。
計算処理を複雑にして難易度を上げたいのはわかるが、正直、良い問題ではない。

大問５（確率）

問題文がやや長め。条件を的確に理解する。
情報の整理→短めに情報をあらわす！

（ア）　44.6％
Ａから１コ目でＸ。
そこから、３の倍数ごとにＰがＸにくる。
約数がでないと左の円をグルグル。
約数がでると右の円でグルグル。
しかし、どちらであっても３の倍数ごとにＰがＸにくるのは変わりない。
出目が〔１＋３の倍数〕のときを調べる。
　
〔１＋３の倍数〕 →【１、４、７、１０】（出目の最高は１２まで）
【１】→大＋小の和の最小は２。×
【４】→（１、３）（３、１）（２、２）
【７】→６通り（サイコロの対面の和）
【１０】→（４、６）（６、４）（５、５）
計１２通り　　→　１２/３６＝１/３

（イ） 　21.5％！
ａがｂの約数だと、右の円に移ってしまう。
ＰをＢにこさせるには、ａがｂの約数でない場合。
Ａから２コすすみ、３の倍数ごとでＰがＢにくる
〔２＋３の倍数〕を調べる　→　【２、５、８、１１】
（ａ、ｂ）の組み合わせ
【２】→（１、１）だと隣の円にいく。×
【５】→（２、３）（３、２）（４、１）
【８】→（３、５）（５、３）（６、２）
【１１】→（５、６）（６、５）
（↑注意すべきは、ｂがａの約数であれば左の円に居続ける。
だから、（４、１）（６、２）が許される。また、ａが１だと自動的に隣に移るので×）
計９通り。　８/３６＝２/９

大問６（空間図形）

（ア）円錐の体積　81.8％
高さＣＯは△ＣＡＯで三平方。
ＣＯ＝√(６²－４²)＝√２０＝２√５ｃｍ
４×４×π×２√５×１/３＝３２√５/３πｃｍ³

（イ）円錐の表面積　51.4％
苦手な人は展開図を書いてみましょ。
○と扇形です。
扇形は〔×半径/母線〕と覚えておこう。
４×４×π＋６×６×π×４/６
＝４０πｃｍ²

（ウ）苦悶の苦問。　6.4％!!
展開図に引き直すと∠ＡＣＤ＝８０°と中途半端な角度がでてしまうので、立体のままで考える。
どこかで三平方が使えないかなぁと三角形も模索。
１２０°という意味深な角度が与えられているので底面積方面に思考を広げる。
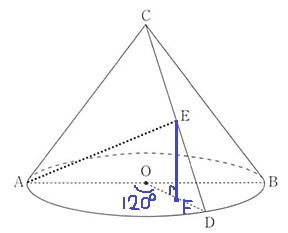
Ｅから垂線をひき、足をＦとく。ＥＦの長さは△ＣＯＤから考える。

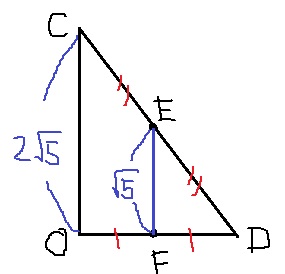
中点連結定理ってヤツですね。
（ア）で円錐の高さがでているので、暗算で出せます。

ＡＦが知りたいところ。
ここで意味深な１２０°を用いる。

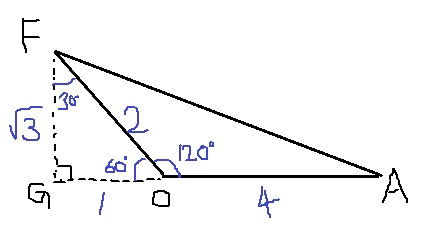
ＡＯの延長線とＦからの垂線の交点をＧとする。
すると、△ＦＧＯが３０°－６０°－１２０°
１：２：√３の直角三角形なので、ＦＧ＝√３
△ＦＧＡで三平方。ＦＡ＝√２８
　
最後に、△ＥＡＦで三平方。
ＥＡ＝√｛(√５)²＋（√２８）²｝＝√（５＋２８）＝√３３ｃｍ
　△ＦＧＯの作り方と、１２０°の活用法は覚えておこう。

大問７（平面図形）

（ア）部分証明　25.5％！
（i）結果に接続するように理由を述べる。
円周角の定理ですね。弧ＢＣに対する円周角です。
(ii)やや慣れが必要。
円周角の定理の逆。
「２点○、○が直線○○について同じ側にあって、∠○○○＝∠○○○ならば、
４点○、○、○、○は同一円周上にある」。
↑長い言い回しだが、覚えておかないと定理が使えない。
　
Ｐ→Ｑ（ＰならばＱ）が成り立つとき、Ｑ→Ｐ（ＱならばＰ）を逆という。
逆は必ずしも真ではないが、円周角の定理については逆も真。
　
円周角の定理の逆をうまく使えれば、”２角が等しい”点から、
新たな円を創造でき、円周角の定理にコンボさせて、
さらに等しい角をみつけることができる。

（イ）　9.1％!!
ここまで到達するのに多くの受検生がバテていると思うが、最後は適度に良い問題。
数字と等しい角度に印をつける。

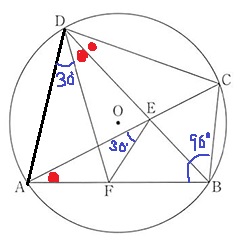
↑前問を利用。●も∠ＡＤＦ＝３０°も円周角の定理。
イメージしにくかったら、ＡＦＥＤに円を書いてもＯＫ
『円に内接する四角形の対角の和は１８０』
∠ＡＤＣ＝１８０－９６＝８４°
３０＋●＋●＝８４
●＝２７°
△ＥＡＦで外角定理。
∠ＢＦＥ＝３０＋２７＝５７°
公立高校入試解説ページに戻る