問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
（２ｘ－３ｙ）/４＋（ｘ＋４ｙ）/６
＝｛３（２ｘ－３ｙ）＋２（ｘ＋４ｙ）｝/12
＝（６ｘ－９ｙ＋２ｘ＋８ｙ）/12
＝（８ｘ－ｙ）/12
（２）
（１＋√６）2－（√８＋10√３）/√２ ←√８/√２＋10√３/√２
＝１＋２√６＋６－２－５√６
＝５－３√６
（３）
（ｘ－７）2－４（ｘ－７） ←Ｘ＝ｘ－７とする
＝Ｘ2－４Ｘ
＝Ｘ（Ｘ－４） ←戻す
＝（ｘ－７）（ｘ－７－４）
＝（ｘ－７）（ｘ－11）＝０
ｘ＝７、11
（４）
ｙ＝－１/４ｘ2は上に凸のグラフ。
ｘ＝－６を代入すると、ｙ＝－１/４×６2＝－９
ということは、ｘ＝ａ（ａ＞０）のとき、最小値ｙ＝－16
－16＝－１/４ａ2
ａ2＝64
ａ＞０より、ａ＝８
ｘ＝０のとき、最大値ｂ＝０
ａ…８、ｂ…０
（５）
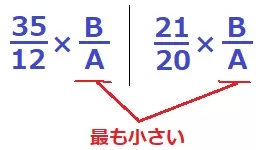
ｘ＝Ｂ/Ａに置き換える。最も小さいＢ/Ａを考える。
まず、Ｂを使って分母の12と20を約分で消す必要がある。
Ｂは12と20の公倍数、分子のＢが最も小さくなるのは最小公倍数。
Ｂ→12と20の最小公倍数である60
分母のＡを大きくするとＢ/Ａは小さくなる。
Ａ→35と21の最大公約数である７
したがって、ｘ＝60/７
（６）
【Ａ】１・３・５
【Ｂ】４・６・８
ａ＝残ったＡ２枚、ｂ＝残ったＢ２枚、ｃ＝取った２枚の和。
条件はａ＜ｃ＜ｂ
ａの最大値は３＋５＝８、ｂの最小値は４＋６＝10なので、ａ＜ｂは必ず成り立つ。
条件が崩れる可能性があるのは、ａ＜ｃかｃ＜ｂ。余事象から攻める。
●ａ＞ｃになる場合
Ａで１を取ると、ａ＝３＋５＝８
８未満となるｃは、１＋４、１＋６の２通り。
Ａで３を取ると、ａ＝１＋５＝６
ｃは最小でも３＋４＝７だから、ａ＜ｃになる。
●ｂ＞ｃになる場合
Ｂで８を取ると、ｂ＝４＋６＝10
11以上となるｃは、８＋３＝11、８＋５＝13の２通り。
Ｂで６を取ると、ｂ＝４＋８＝12
ｃは最大でも５＋６＝11だから、ｃ＜ｂになる。
余事象は４通り、全体は３×３＝９通りだから確率は５/９。
（７）
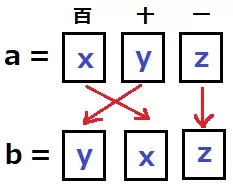
ａの百の位をｘ、十の位をｙ（ｙ≠０）、一の位をｚとする。
ａ－ｂ
＝（100ｘ＋10ｙ＋ｚ）－（100ｙ＋10ｘ＋ｚ）
＝90ｘ－90ｙ
＝90（ｘ－ｙ）
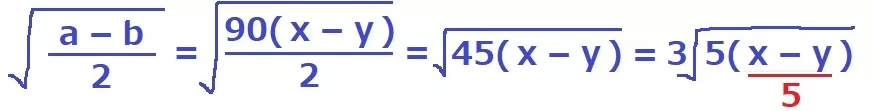
（ａ－ｂ）に90（ｘ－ｙ）を代入して変形するとこうなる。
自然数になる→ルートを外すには、ｘ－ｙ＝５（＊√５×√５＝５）
ｙ≠０と合わせると、（ｘ、ｙ）＝（９、４）（８、３）（７、２）（６、１）
ｘ＋ｙ＋ｚ＝20より、ｚ≦９と合わせると（ｘ、ｙ、ｚ）＝（９、４、７）（８、３、９）
よって、839と947。
（８）
答案では途中の式を含めて求め方を説明する。
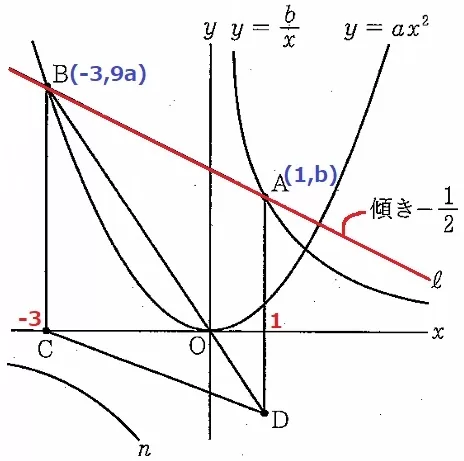
直線ℓの傾き－１/２に注目する。
Ｂ（－３、９ａ）→Ａ（１、ｂ）
右に４、下に（ｂ－９ａ）だから、傾きで等式を立てると、（ｂ－９ａ）/４＝－１/２
４倍して、－９ａ＋ｂ＝－２ …①
赤線の∽、もしくはＢＯ；ｙ＝－３ａｘにｘ＝１を代入して、
Ｄ（１、－３ａ）
四角形ＡＢＣＤの面積で等式。
（９ａ＋ｂ＋３ａ）×４÷２＝17
12ａ＋ｂ＝17/２
24ａ＋２ｂ＝17 …②
②－①×２をすると、42ａ＝21
ａ＝１/２
①に代入、－９×１/２＋ｂ＝－２
ｂ＝５/２
ａ…１/２、ｂ…５/２
大問２（平面図形）
（１）①
半径２ｃｍ、中心角ａの扇形の面積を求める。
２×２×π×ａ/360＝１/90πａｃｍ2
②
△ＢＤＯ∽△ＡＥＣの証明。
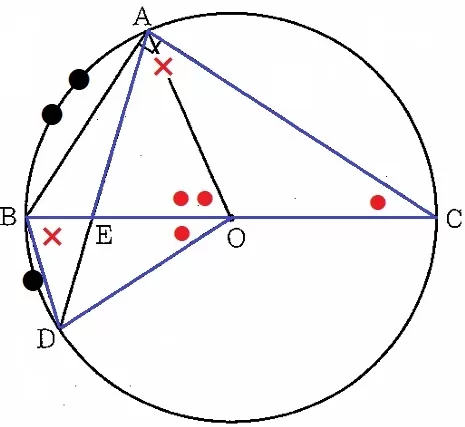
弧ＤＣに対する円周角より、∠ＤＢＯ＝∠ＥＡＣ（×）
中心角の大きさは弧の長さに比例する→２∠ＢＯＤ（●）＝∠ＡＯＢ（●●）
円周角は中心角の半分だから、∠ＡＣＥ＝１/２∠ＡＯＢ（●●）＝●
∠ＢＯＤ＝∠ＡＣＥ
２角が等しいので∽。
（２）①
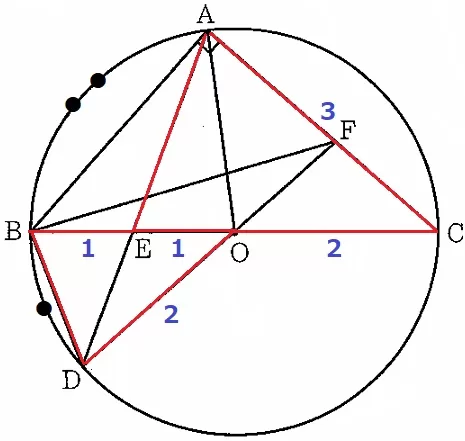
∠ＢＡＣ＝90°、ＢＣ＝４ｃｍから、△ＡＢＣで三平方を使えばＡＢが求まる。
ＡＣの長さが知りたい。
先ほどの△ＢＤＯ∽△ＡＥＣより、△ＢＤＯはＢＯ＝ＤＯ（半径）で二等辺だから、
これと相似にある△ＡＥＣも二等辺である。
ＡＣ＝ＥＣ＝３ｃｍ
△ＡＢＣで三平方→ＡＢ＝√７ｃｍ
②
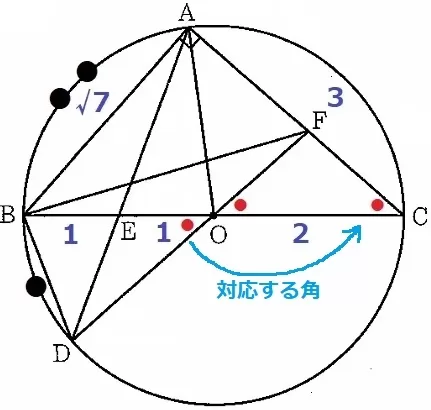
角度から図形の性質をさぐる。
対頂角と前問の∽の対応する角より、△ＦＯＣは２つの底角が等しい二等辺三角形。
ＡＦ：ＦＣに目が行きやすいが、直接ＢＦを斜辺とする直角三角形をつくってしまう。
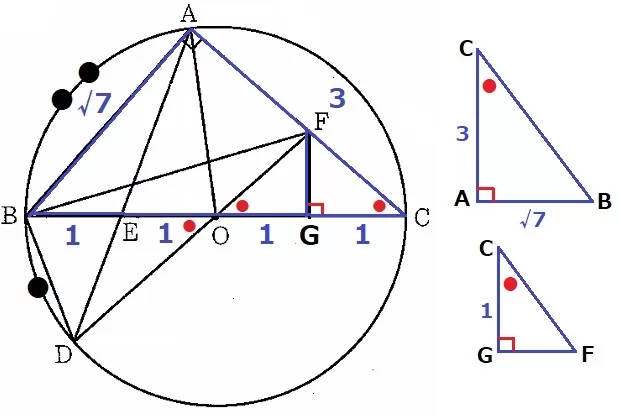
Ｆから垂線をひき、足をＧとする。
△ＦＯＣは二等辺だから、ＯＧ＝ＧＣ＝１ｃｍ
共通角と直角の２角相等より、△ＡＢＣ∽△ＧＦＣ
ＣＡ：ＢＡ＝ＣＧ：ＦＧだから、ＦＧ＝√７×１/３＝√７/３ｃｍ
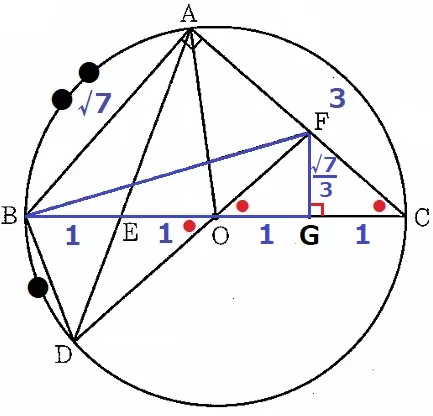
△ＢＦＧで三平方→ＢＦ＝２√22/３ｃｍ
＠別解＠
まだ何かないか、別の角度から分析してみました。
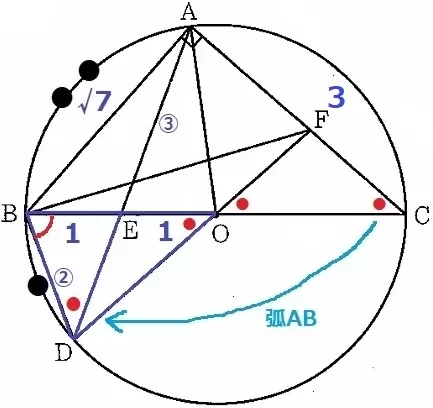
△ＢＤＯ∽△ＡＥＣの対応する辺であるＢＤ：ＡＥ＝②：③とする。
弧ＡＢに対する円周角から、∠ＡＤＢ＝●
２角相等で△ＢＤＯ∽△ＢＥＤより、△ＢＥＤも二等辺三角形。
ＤＥ＝②
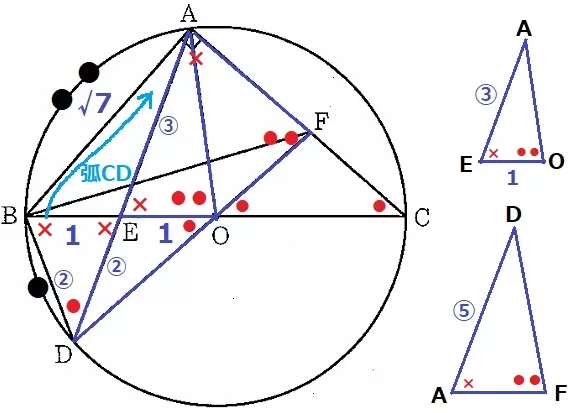
二等辺三角形ＢＥＤの底角を×とする。
対頂角で∠ＡＥＯ＝×、弧ＣＤに対する円周角で∠ＤＡＦ＝×
弧ＡＢ＝２×弧ＢＤ→∠ＡＯＥ＝●●、△ＯＣＦで外角定理→ＤＦＡ＝●●
２角相等により、△ＡＥＯ∽△ＤＡＦ
ＥＯ：ＡＦ＝ＡＥ：ＤＡだから、ＡＦ＝１×⑤/③＝５/３ｃｍ
△ＡＢＦで三平方→ＢＦ＝２√22/３ｃｍ
大問３（空間図形）
（１）①
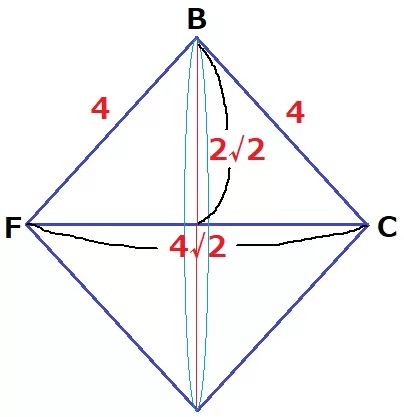
△ＢＣＦは直角二等辺→辺の比は１：１：√２、ＦＣ＝４√２ｃｍ
回転体は底面が半径２√２ｃｍの円、高さの合計４√２ｃｍの円錐である。
２√２×２√２×π×４√２÷３＝32√２/３πｃｍ3
②
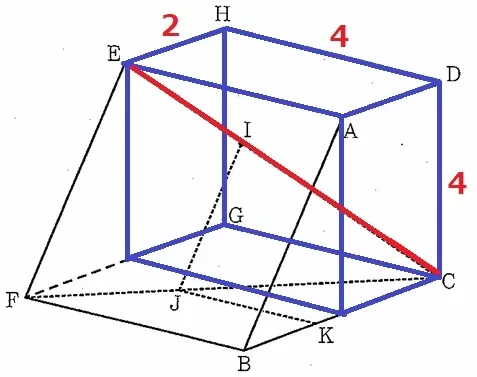
ＥＣを対角線とする直方体に目を向ける。
ＥＣ＝√（２2＋４2＋４2）＝６ｃｍ
③
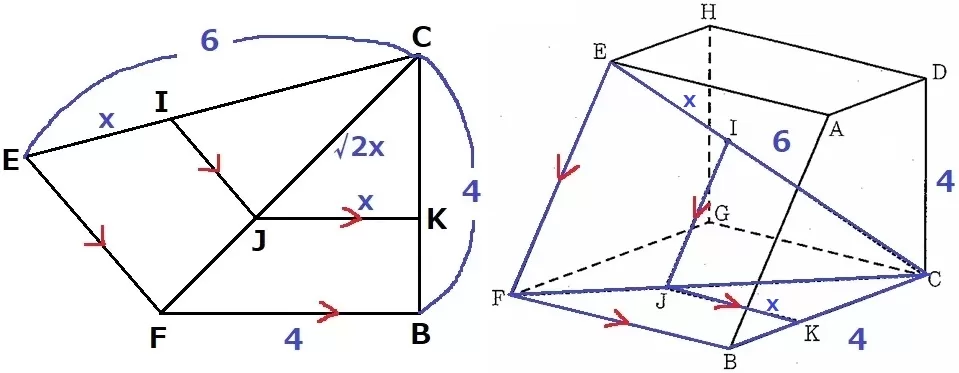
離れている辺の長さが等しい。２つの面を展開する。
平行線から、△ＣＩＪ∽△ＣＥＦ、△ＣＪＫ∽△ＣＦＢ。
ＥＩ＝ＪＫ＝ｘとする。
△ＣＦＢは直角二等辺→相似から△ＣＪＫも直角二等辺なので、ＣＪ＝√２ｘ
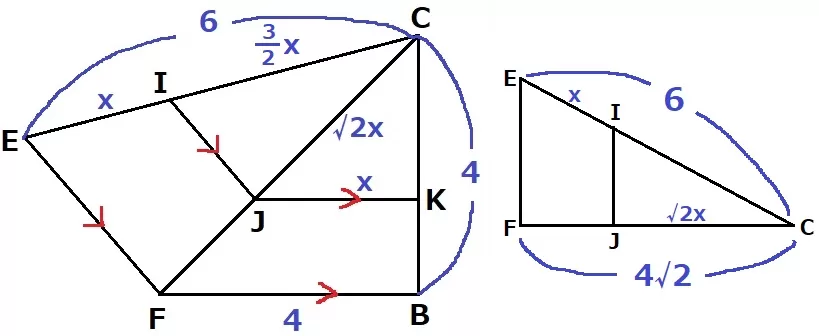
ＣＦ＝４√２ｃｍ
ＩＣ：ＪＣ＝ＥＣ：ＦＣだから、ＩＣ＝√２ｘ×６/４√２＝３/２ｘ
ＥＣ＝ｘ＋３/２ｘ＝５/２ｘ＝６
ｘ＝６÷５/２＝12/５ｃｍ
（２）①
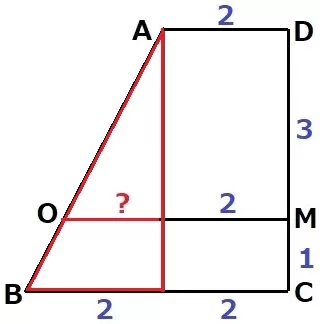
Ａから垂線をおろし、２ｃｍもおろす。
左側の赤線で∽、？＝２×３/４＝３/２ｃｍ
ＯＭ＝３/２＋２＝７/２ｃｍ
②
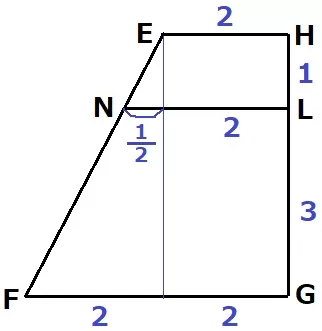
同様にＮＬを求めると、ＮＬ＝１/２＋２＝５/２ｃｍ
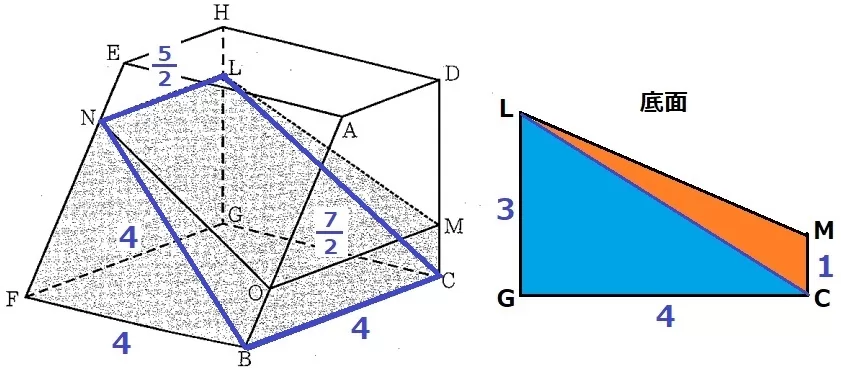
立体を面ＮＢＣＬで分割して、断頭三角柱で体積を求める。
底面は背後の四角形ＬＧＣＭで捉えるとわかりやすい。
立体ＮＦＢ－ＬＧＣ…底面は△ＬＧＣ、高さはＮＬ・ＦＧ・ＢＣの平均
立体ＮＢＯ－ＬＣＭ…底面は△ＬＣＭ、高さはＮＬ・ＢＣ・ＯＭの平均
求積すべき立体の体積は、
３×４÷２×（５/２＋４＋４）/３＋１×４÷２×（５/２＋７/２＋４）/３
＝21＋20/３＝83/３ｃｍ3
大問１
（２）後半はそれぞれの分子に÷√２がいいかな？
（５）中学受験でも出題される。
（６）条件が複雑だが、９通りしかないので総当たりで調べてもいい。
ａ＜ｂが必ず成り立つとわかれば、ａとｃ、ｂとｃの兼ね合いを調べればＯＫ。
（７）比較的取りやすいかなと。
ａ－ｂをｘｙｚを用いて示す。ｙ≠０に注意！
（８）手順をきちんと追えるか。
グラフ上にあるＡ、Ｂの座標を文字で表す。未知数がａ、ｂの２種類→連立
１つはℓの傾き、もう１つは四角形ＡＢＣＤの面積から立式する。
大問２
（１）②証明は難しくない。
（２）②迷子になりやすい。ポイントは△ＦＯＣが二等辺であること。
Ｆは二等辺の頂角の頂点。Ｂは底辺ＯＣの延長線上にある。
ここから二等辺を垂直に二等分して三平方に持ち込む。形で覚えてしまった方が早い。
大問３
（１）③離れている辺をｘとする。どっちから攻めるべきか。
△ＣＪＫが直角二等辺なので、ＪＫ側からスタートするとＣＪ＝√２ｘとスッキリする。
（２）②お馴染みの断頭。背面が底面ＢＣＧＦに対して垂直なのがありがたかった。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント
今年のC問題めっちゃ簡単じゃないですか?問われ方も比較的単純で、時間もかなり余りますし。πのつけ忘れなど単純なミスをしないようにしたいですね。まあ一番難しかったのは間違いなく2017年のときでしょうが。
コメントありがとうございます。
2017年はヤバそうな臭いがしました(;´Д｀)公立入試の世界でも年度や場所によって教委会のやらかしが見受けられます。
今年の大阪は構成は例年通りでしたが、平均点はあがりそうです。とくに空間は正答率が高くなると思います(´ω`)