2019年度　大分県公立高校過去問【数学】解説

平均24.7点（60点満点；平均約41％）


問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）①　95.9％
－６－１＝－７

②　83.6％
－３²－（－２）³
＝－９－（－８）
＝－９＋８＝－１

③　89.0％
６ａ＋ｂ－（３ａ－５ｂ）
＝６ａ＋ｂ－３ａ＋５ｂ
＝３ａ＋６ｂ

④　84.0％
（２ｘ＋ｙ）/３＋（５ｘ－７ｙ）/６
＝（４ｘ＋２ｙ＋５ｘ－７ｙ）/６
＝（９ｘ－５ｙ）/６

⑤　63.0％
（√６＋√３）²
＝６＋２√18＋３
＝９＋６√２

（２）　64.0％
ｘ（ｘ－３）＝２
ｘ²－３ｘ－２＝０
因数分解ができないので解の公式。
ｘ＝（３±√17）/２

（３）　15.0％！
小数第１位を四捨五入したとき、130となるａの範囲を不等式で表す。
129.5の５を四捨五入すると、繰り上がりで130となる。
130.5の５を四捨五入すると、繰り上がりで131になってしまうのでその手前まで。
よって、129.5≦ａ＜130.5
*四捨五入の近似値は、○≦ａ＜○となる。５に注目するとやりやすい。
129.5≦ａ≦130.4とする誤答が多かった模様。

（４）　11.8％！
一次方程式。前半はｘｍ、後半は1200－ｘｍ。
時間＝道のり÷速さ
ｘ/60＋（1200－ｘ）/120
＝（ｘ＋1200）/120分間
*ｘ/６０＋（1200－ｘ）/120と最後まで計算していない誤答が目立つ。

（５）　49.7％
すべての場合→５×５＝25通り
和が３の倍数となる場合を調べる。
３→（１、２）（２、１）
６→（１、５）（５、１）（２、４）（４、２）（３、３）
９→（４、５）（５、４）
計９通り
よって、９/25

（６）　66.8％

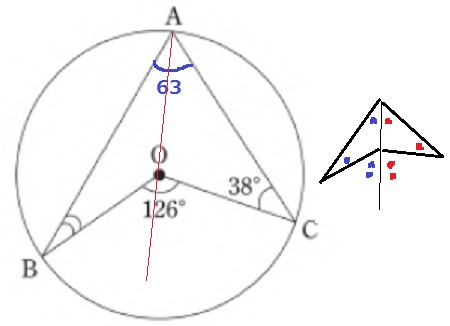
円周角定理より、∠ＢＡＣ＝126÷２＝63°
外角定理より、ブーメラン型の股の角度は３角の和になる。
∠ＡＢＯ＝126－（63＋38）＝25°

（７）　２点－9.8％!!　１点－1.0％
２つの線分からの距離が等しい。

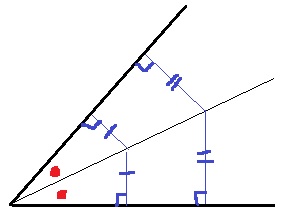
頭の中でこの図がよぎるようにしたい。
角の二等分線上の点から２本の線分までの距離は等しい。
①ＡＢとＣＤを延長、交点をつくる。
②角の二等分線を作成、ＭＮとの交点が点Ｐとなる。

大問２（関数）

（１）　72.8％
ｙ＝ｘ＋１からＡの座標を確定。
Ａ（２、３）
ｙ＝ａ/ｘに放り込む。
３＝ａ/２
ａ＝６

（２）　36.6％
ｙ＝６/ａより、Ｂ（６、１）
原点０を通るので、ｙ＝１/６ｘ

Ｃはｙ＝ｘ＋１とｙ＝１/６ｘの交点。
ｘ＋１＝１/６ｘ
ｘ＝－６/５
ｙ＝－６/５＋１＝－１/５
Ｃ（－６/５、－１/５）

（３）　13.1％！
湾曲部分が厄介。ＡＢに直線をひいてしまおう。

つまるところ、面積の等しい２つの図形に湾曲部分を足しても面積は等しくなるので、
△ＡＣＢと△ＡＤＢの面積が等しい。
ＡＢの傾きを求める。
Ａ→Ｂ：右に４、下に２だから、傾きは－１/２
ＣＤの傾きも－１/２。
－６/５＝－１/２×－１/５＋ｂ
ｂ＝－４/５
Ｄのｙ座標は－４/５。

大問３（数量変化）

（１）　ア：71.4％、イ：55.9％
投影距離の画面の長さの関係をとらえる。

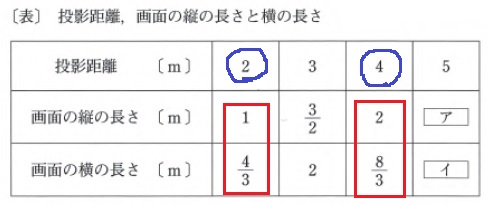
２ｍと４ｍがわかりやすい。
投影距離が２倍になれば、画面の長さも２倍。つまり、比例。
ア＝１×５/２＝５/２
イ＝４/３×５/２＝10/３

（２）　24.3％！
実際に表でまとめてみよう。

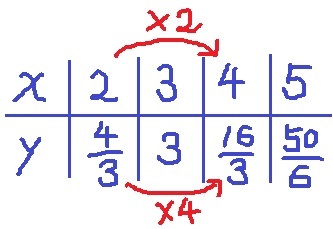
ｘが２倍になるとｙが４倍になっている。
ここから、ｘとｙの関係はｙ＝ａｘ²と推測。
４/３＝２²ａ
ａ＝１/３
ｙ＝１/３ｘ²
試しに他の値を代入してみると、関係性が成り立っている。
*投影距離と縦の長さが比例。投影距離と横の長さ比例。
面積＝縦×横だから、投影距離と面積の関係は放物線で上昇するのでは？と考えられる。

（３）　1.6％!!
１つずつ丁寧に紐解いていく。
前問より、ｙ＝１/３ｘ²
投影距離が３/２ｍのときの画面の面積は、
ｙ＝１/３×（３/２）²＝３/４ｍ²
面積を２倍にすると３/２ｍ²。

このときの投影距離は、
３/２＝１/３ｘ²
ｘ²＝９/２
ｘ＞０より、ｘ＝３√２/２
投影距離は３√２/２ｍ。

基準では、視聴距離が画面の対角線より長いと見やすいとある。
そこで、画面の対角線に注目する。

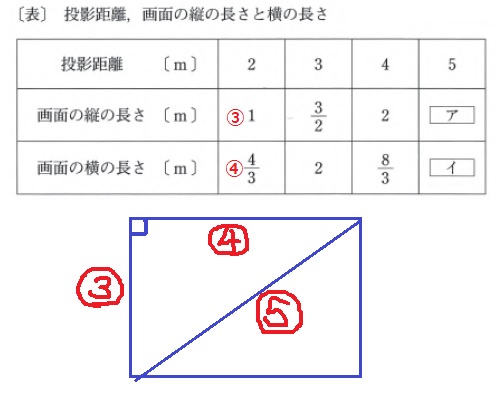
縦：横＝１：４/３＝３：４
縦③、横④とすると、３：４：５から対角線の長さは⑤となる。
投影距離が３√２/２ｍのときの⑤が答えとなる。

表をみると、投影距離の半分が画面の縦の長さだから、
③＝３√２/２÷２＝３√２/４
⑤＝３√２/４×５/３=５√２/４
したがって、視聴距離は５√２/４ｍより長いとよい。
投影距離・画面の面積・縦・横・対角線の関係を適切に把握すること！
*画面のサイズがインチが使われる。
１インチ（inch）＝2.54ｃｍ
インチは対角線の長さを示す。
縦横の比率は３：４が主流だったが、現在は９：16も増えたようだ。

大問４（方程式）

（１）　64.7％
無作為に取り出した150個のうち、５個の印があった。
全部：印あり＝150：５＝30：１
この比率は母集団も変わらないとみなす。
印は100個つけたので、100×30/１＝3000個

（２）①　8.8％!!
Aは3000個製造。うち２％にあたる60個が不良品。
Bはｘ個製造したとする。不良品は0.5％だから、５/1000ｘ個。
不良品の数で等式を作成する。
60＋５/1000ｘ＝（3000＋ｘ）×14/1000
60000＋５ｘ＝42000＋14ｘ　←すべてを1000倍。桁ミス注意！
ｘ＝2000
Ｂは2000個製造した。

＠別解＠
中学受験の天秤法を使うとラクラク。
問題文を食塩水の濃度問題に置き換えると、
『0.5％の食塩水？ｇと2.0％の食塩水を混ぜたら1.4％になった。？は何ｇか』

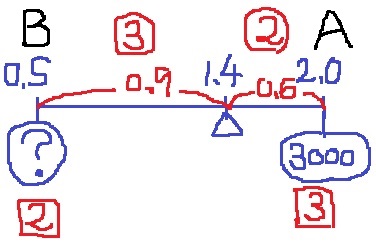
支点を1.4％とする。
支点からの距離が３：２なので、食塩水の重さは２：３
？＝3000×２/３＝2000

②　4.5％!!
連立方程式。
Ａをｘ台、Ｂをｙ台とする。
製品の製造個数から、3000ｘ＋2000ｙ＝18000…①
不良品の個数から、3000ｘ×２％＋2000ｙ×0.5％＝18000×１％…②

簡単になおすと、
３ｘ＋２ｙ＝18…①’
６ｘ＋ｙ＝18…②’
これを解いて、ｘ＝２、ｙ＝６
Ａは２台、Ｂは６台。

大問５（空間図形）

（１）　59.9％
△ＡＢＣは１：１：√２の直角三角形。
三平方より、ＡＣ＝６√２
ＡＨ＝６√２÷２＝３√２ｃｍ

（２）　46.8％
△ＯＡＨで三平方→ＯＨ＝３√２（△ＯＡＨは直角二等辺）
６×６×３√２÷３＝36√２ｃｍ³

（３）①　15.0％！
あふれた水の体積＝正四角錘が沈んだ体積。

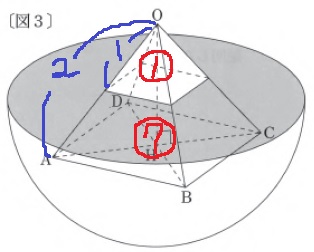
体積比は辺の比の３乗。
水なし：水あり＝１³：２³－１＝１：７
36√２×７/８＝63√２/２ｃｍ³

②　1.0％!!!
球の半径を求めるので、球の中心点を確定する。

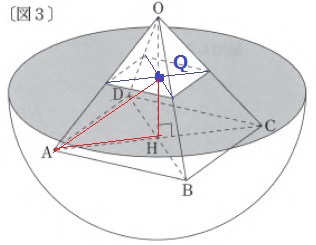
球の中心点は球の断面である、半球の水面の中心にある。
一方、正四角錘ＯＡＢＣＤは、その底面ＡＢＣＤが水面と平行のまま沈ませるので、
Ａ・Ｂ・Ｃ・Ｄがそれぞれ半球に接したとき、球の中心点はＯＨ上にくる。
ＯＨ上で、かつ水面と交わる交点が球の中心点Ｑとなる。
（水面を断面としたとき、正四角錘の断面である小さな正方形の中心点に等しい）

△ＱＡＨに着目。
ＡＨ＝３√２ｃｍ
ＱＨ＝ＯＨ÷２＝３√２÷２＝３√２/２ｃｍ
三平方の定理→ＱＡ＝３√10/２ｃｍ

大問６（平面図形）

（１）　88.1％
中点連結定理の形。ＰＱ＝ＡＣ÷２＝３ｃｍ

（２）①　３点－8.8％!!　２点－2.0％　１点－6.8％
四角形ＰＱＲＳが平行四辺形である証明。

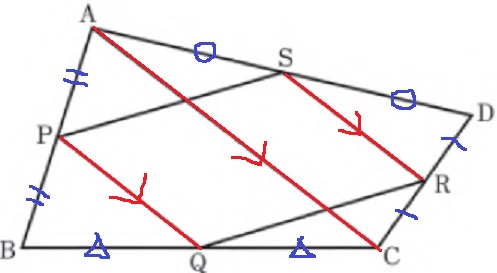
ＡＣを境に、△ＡＢＣと△ＡＤＣで中点連結定理が成立する。
ＰＱ//ＡＣ//ＳＲとなり、ＰＱとＳＲはＡＣの半分の長さで等しい。
１組の対辺の長さが等しく、かつ平行だから四角形ＰＱＲＳは平行四辺形。

②Ⅰ　32.6％！
平行四辺形ＰＱＲＳが正方形になるための条件を答える。
平行四辺形から正方形に変えるには、隣り合う辺の長さが等しく、かつ直角に交わる。
→ＰＱ⊥ＰＳ、ＰＱ=ＰＳ（イ）

Ⅱ　２点－1.0％!!!　１点－2.2％
指定された作図方法を使うと、四角形ＰＱＲＳが正方形となる理由を記述する。
変則的な証明問題で難易度は高い:;(∩´＿`∩);:

とりあえず、作図してから考える。

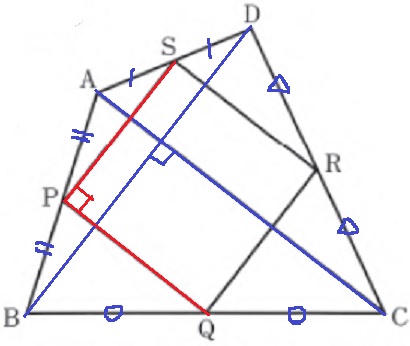
ＡＣ⊥ＢＤ、ＡＣ＝ＢＤ
赤いところ（ＰＱ⊥ＰＳ、ＰＱ=ＰＳ）が証明したい点。

前問では、△ＡＢＣと△ＡＤＣで中点連結定理を利用して、
ＰＱ//ＳＲ、ＰＱ＝ＳＲから、四角形ＰＱＲＳが平行四辺形と導いた。

△ＡＢＤに注目すると、ここも中点連結定理の形になっている。
ＰＳはＢＤの半分。ＢＤ＝ＡＣで、ＡＣの半分がＰＱだから、
これらをつなぎ合わせると、ＰＱ＝ＰＳとなる。

角度は平行線を活用する。
ＡＣ⊥ＢＤで、ＡＣ//ＰＱから、ＰＱ⊥ＢＤ。
さらに、ＢＤ//ＰＳから、ＰＱ⊥ＰＳ。
ＰＱ⊥ＰＳ、ＰＱ＝ＰＳとなり、正方形の証明が完成する。

*記述の仕方を研究しておこう。以下、公式解答。
△ＡＢＣにおいて、点Ｐ、Ｑはそれぞれ辺ＡＢ、ＢＣの中点だから、中点連結定理より、
ＰＱ//ＡＣ、ＰＱ＝1/2ＡＣ
△ＡＢＤにおいて、点Ｐ、Ｓはそれぞれ辺ＡＢ、ＡＤの中点だから、中点連結定理より、
ＰＳ//ＢＤ、ＰＳ＝1/2ＢＤ

ＡＣ⊥ＢＤ、ＰＱ//ＡＣより、平行線の同位角は等しいから、ＰＱ⊥ＢＤ
また、ＰＱ⊥ＢＤ、ＰＳ//ＢＤより、平行線の同位角は等しいから。ＰＱ⊥ＰＳ

ＡＣ＝ＢＤ、ＰＱ＝1/2ＡＣ、ＰＳ＝1/2ＢＤから、ＰＱ＝ＰＳ
公立高校入試解説ページに戻る