平均51.9点(前年比;-4.0点)
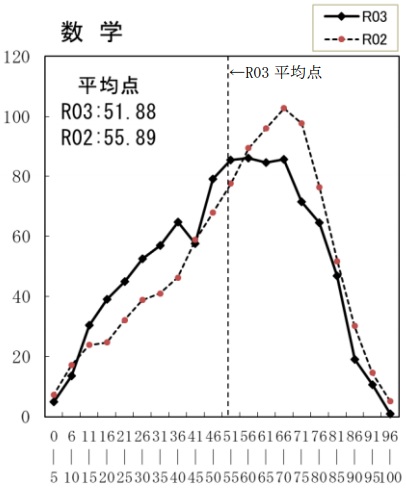
100点―1名、0点―2人
問題はこちら→東進ハイスクールさん(解答)
出題範囲の縮小は三平方の定理と標本調査。
大問1(小問集合)
(1)
(-3)+(-1)
=-3-1
=-4
(2)
(15x+5)÷5 ←分配法則
=15x÷5+5÷5
=3x+1
ウ
(3)
√50-√8
=5√2-2√2
=3√2
(4)
x2+4x=2
x2+4x-2=0
解の公式を適用。xの係数が偶数なので、b=2b’が使える。
x=-2±√6
@別解@
平方完成でもOK。
x2+4x=(x+2)2-4
(x+2)2-4=2
(x+2)2=6
x+2=±√6
x=-2=±√6
(5)
有理数→整数の分数で表せる数、無理数→整数の分数で表せない数
ア:0.7=7/10(有理数)
イ:-1/3(有理数)
ウ:円周率π=3.14159265…と数字が不規則に並ぶ無限小数。(無理数)
エ:√10(無理数)
オ:-√49=-7=-7/1(有理数)
ウ・エ
(6)
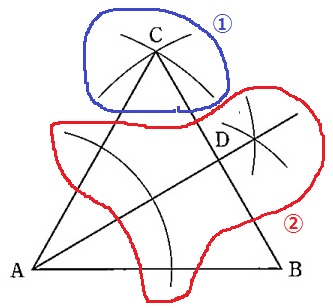
①ABの長さをとり、AとBそれぞれに針を合わせて線をひく。
交点がCで、△ABCは3辺が等しい正三角形。
②DはBC上の点。
DAは∠CABの二等分線で、これとBCとの交点がDとなる。
(8)
子供の人数
*x個のアメを3個ずつ配ると22個余った。
→(x-22)/3人
x個のアメを4個ずつ配ると6個足りない。
→(x+6)/4人
過不足に気を付けよう。
配る予定のアメの数は、余りは余計なので引く。足りない分は足す。
(9)
3人に順番を付けて並ばせる(順列)→3×2×1=6通り
1番目が学、2番目が春、3番目が桜は1通りしかない。
確率は1/6
(10)
てこのモーメント。
〔おもりの重さ×支点からの距離〕が左右で等しいと、てこが釣り合う。
反比例の比例定数aは積xyで一定である。
本問の反比例の式はy=1000/x
イ
(11)
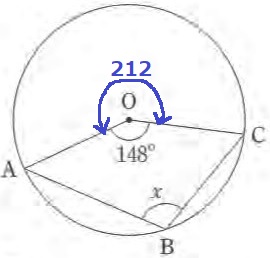
360-148=212°
円周角は中心角の半分。
x=212÷2=106°
(12)
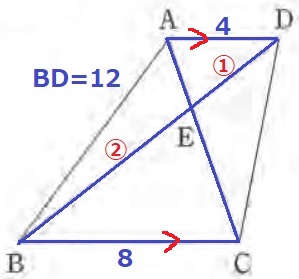
AD//BC→対頂角と錯角で2角が等しい。△ADE∽△CBE
DE:BE=4:8=①:②
BE=12×②/③=8cm
大問2(小問集合2)
Ⅰ(1)
ア:範囲(レンジ)=最大値-最小値
西回りの範囲は、35-25=10
東回りの範囲は、51-20=31
→東回りの方が範囲が大きい。
また、西回りは平均値、中央値、最頻値がほぼ同じで正規分布に近いと思われる。〇
イ:最も多くあらわれる値→最頻値(モード)
西回りは29分、東回りは24分×
ウ:中央値(メジアン)で判断する。西回りは28分だが、東回りは24分。×
(2)
2つの度数分布多角形が似た形をしており、
平日の方が休日より左側にあるから。
*説明問題。
休日の波を左に移動させると平日の波とほぼ重なる。
Ⅱ(1)①
円錐の体積は、円柱の体積の1/3倍。
②
答案では理由も記述する。
PとQの体積を比較すればいい。比を用いると比較が楽になる。
球の体積は4/3πr3、半球はこの半分。
P:Q
=(4/3π×43×1/2):(1/3π×42×8)
=1:1
→体積は等しい。
ア
(2)①
左右の半円をくっつけて1つの円にする。
カーブの部分は2πrm。
これにストレート部分の2amを足せばいい。
2πr+2am
②
ストレート部分の長さは等しいので、差が出るのはカーブ。
第1レーンのカーブは前問の2πr
第2レーンの半径は(r+1)mだから、
カーブの長さは2π(r+1)=2πr+2π
差は、(2πr+2π)-2πr=2πm
③
前問の答えから考える。
第2レーンのスタート位置は第1レーンの2πm前方にある。
『2π』は半径rの変数を含まない定数。
つまり、スタート位置は半円の長さや長方形の横の長さに関係なく決まる。
ウ
*第3レーンのスタート位置は第2レーンの2πm前方となる。
大問3(数量変化)
Ⅰ(1)
桜が出発した16時5分のとき、グラフから守は400mの地点にいる。
400m
(2)
2直線の交点が0≦y≦600にないので、桜は守に追いつけない。
*交点で2人が会うので、交点がなければ追いつけないことになる。
直線を延長すれば交点ができる。必ずyの変域を指摘すること!
(3)
(1)より、5分後の両者の距離は400m。
ここから守は分速100m、桜は分速200mで近づくので、1分あたり300m縮まる。
400÷300=4/3分=1分20秒
16時5分の1分20秒後である16時6分20秒。
Ⅱ(1)
格子点を探す。
サボは(20、100)をy=ax2に代入しました。
100=202a
a=1/4
y=1/4x2
(2)
x=10のとき、y=25
x=20のとき、y=100
平均の速さ=距離の差÷時間の差
=(100-25)÷(20-10)
=秒速15/2m
@別解@
y=ax2において、xの値がp→qに増加するときの変化の割合はa(p+q)
1/4(10+20)=15/2
(3)①
〔時速km〕を×10/36すると〔秒速m〕に変わる。
時速45km×10/36=秒速25/2m
→10秒で125m進む。

原点と(10、125)を結ぶ。
右に1進むと、上に5あがる傾きとなる。
②
先ほどのグラフで交点が(50、625)だから50秒後。
③
説明問題。
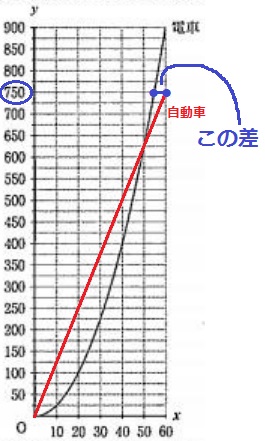
750m地点⇒y=750
y=750のときのxの値の差を求めればいい。
大問4(平面図形)
Ⅰ(1)
四角形AFCEが平行四辺形である証明。
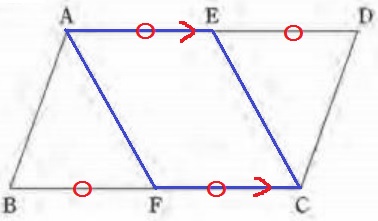
平行四辺形の対辺は等しいので、AD=BC
EとFはそれぞれの中点だから、AE=FC
平行四辺形の対辺は平行なので、AD//BC
→AE//FC
1組の対辺の長さが等しく、かつ平行だから四角形AFCEは平行四辺形。
あ…イ、い…ア、う…1組の向かい合う辺
(2)
△ABF≡△CDEの合同条件を書く。
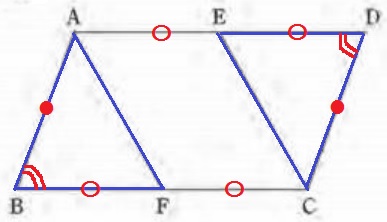
E、Fは平行四辺形の1辺の中点→BF=DE
平行四辺形の対辺は等しい→AB=CD
平行四辺形の対角は等しい→∠ABF=∠CDE
合同条件は、”2辺とあいだの角が等しい”
Ⅱ(1)
△ABR∽△CPSの証明。
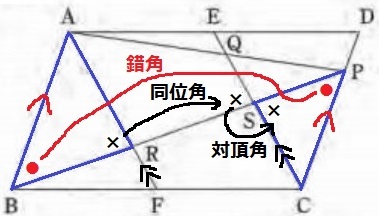
AB//DCより、錯角から∠ABR=∠CPS…①
解答はこれ以降を記述する。もう1つの等角を指摘できれば証明できる。
四角形AFCEが平行四辺形であることは証明済みなので、
AF//ECから同位角より、∠ARB=∠QSR
対頂角で、∠QSR=∠CSP
つなげると、∠ARB=∠CSP…②
①、②より、2角が等しいから∽
(2)
PS:SBを求める。
PSとBRはそれぞれ△CPSと△ABRの1辺なので、
先ほどの△ABR∽△CPSを活用する。
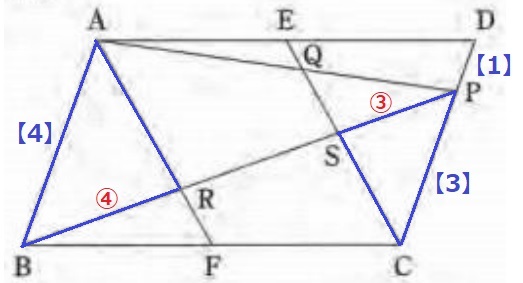
DP=【1】、PC=【3】とする。
平行四辺形の対辺から、AB=【4】
△ABRと△CPSの相似比は、AB:CP=BR:PS=④:③
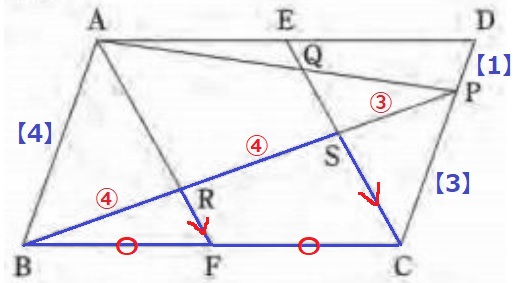
RF//SCより、△BRF∽△BSC
BR:RS=BF:FC=1:1
RS=④
PS:SB=③:⑧
PSはSBの3/8倍。
(3)
いままでの相似比を手がかりにする。
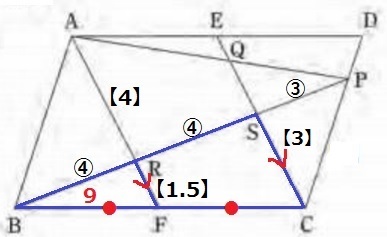
相似比からAR=【4】、CS=【3】
△BRF∽△BSCより、RF=【3】÷2=【1.5】
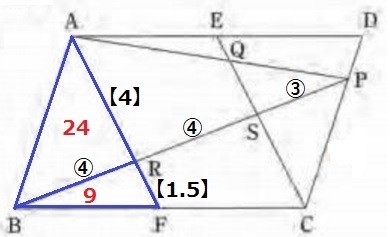
△ABR:△RBF=AR:RF=【4】:【1.5】=8:3
△ABR=9×8/3=24cm2
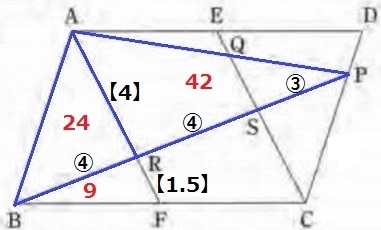
△ABR:△APR=BR:RP=④:⑦
△APR=24×⑦/④=42cm2
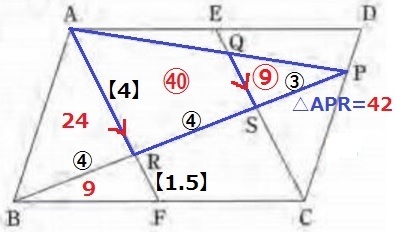
面積比は相似比の2乗。
△APR…⑦×⑦=㊾
△QPS…③×③=⑨
四角形ARSQ…㊾-⑨=㊵
四角形ARSQの面積は、42×㊵/㊾=240/7cm2
Ⅲ
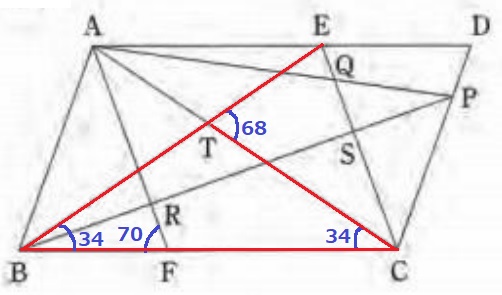
△TBCで外角定理。
∠TBC=68-34=34°
△TBCは2つの底角が等しく、二等辺三角形。
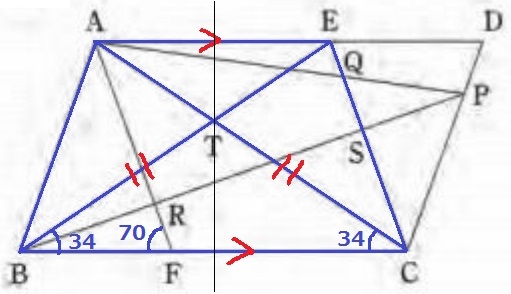
AE//BCだから、四角形ABCEは台形。
Tは台形の対角線ACとBEの交点である。
△TBCが二等辺三角形で左右対称だから、台形全体も左右対称。
→台形ABCEは等脚台形。
(錯角や対頂角から△TAEも二等辺三角形で左右対称)
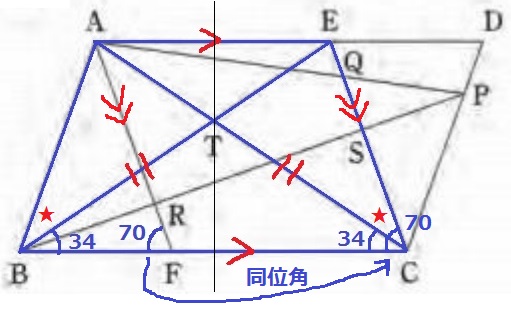
対称性から、∠ABT=∠ECT
AF//ECの同位角で、∠ECF=70°
∠ECT=70-34=36°
∠ABT=36°
●講評●
大問1
いずれも基本なので失点をおさえたい。
(9)自動的に学は1位で1通りしかない。
大問2
問題文の読解に時間をかけ過ぎないように。
Ⅰ(1)値が分散するとはどういうことか。
(2)『形が似ている&平日が左にある』がポイント。
Ⅱ(2)②第2レーンはrをr+1に変える。
③計算結果に変数を含まない⇒定数⇒半径や長さに関係なく決まる。
大問3
Ⅰ(2)y変域を忘れずに。
Ⅱここも要点を指摘すれば、それほど文字数は多くなくて済む。
大問4
Ⅰ(2)別の証明ルートで必要な合同条件を指摘するというユニークな設問であった。
Ⅱ(2)何倍になるか→比の問題。証明済みの相似を活用する。
(3)前問をクリアしていないと無理。
RS:SP=4:3がわかっているので、△APR:△QPS=49:9を利用した。
Ⅲラストが角度の設問であった。
二等辺三角形から左右対称をつかむ。



コメント