平均48.0点(前年比;-0.8点)
問題はこちら→東進ハイスクールさん(解答)
出題範囲の除外は標本調査。
大問1(小問集合)
(1)①
2-(-5)
=2+5
=7
②
4x-2x×1/2
=4x-x
=3x
③
-6a3b2÷(-4ab)
=3/2a2b
(2)
(2x-y-6)+3(x+y+2)
=5x+2y ←代入
=5×(-2)+2×3
=-4
(3)
ネジレ…延長しても交わらない、かつ平行でもない。
辺CF、辺DF、辺EF
(4)
√24=2√6
根号のなかが平方数になれば、根号が外れて自然数になる。
n=6
(5)
反比例の比例定数aは積xyで一定。
a=2×(-2)=-4
y=-4/x
(6)
三平方の定理で、BC=√13cm
(7)
20人の中央値(メジアン)は10番目と11番目の平均。
中央値が50回ということは、11番目~20番目は50回以上。
→50回以上は少なくとも10人いる。
エ
(8)
説明問題。
はじめのAの量をxmLとすると、Bの量は2xmL
(x+140):2x=5:3
外項と内項の積より、
3(x+140)=2x×5
7x=420
x=60
60mL
(9)
y=ax2において、xの値がp→qに増加するときの変化の割合はa(p+q)
変化の割合は、1/2(1+3)=2
グラフで示すとx軸は時間、y軸は距離。
距離÷時間で求まる傾き(変化の割合)は平均の速さにあたる。
*(1、1/2)と(3、9/2)を結んだ直線の傾き。
エ
大問2(図形の性質)
(1)
平行四辺形は対角線が各々の中点で交わり、
2組の対辺が等しく、2組の対角も等しいから、ア・エ・オが自ずと消える。
長方形は4つの角が等しい⇒平行四辺形の隣り合う角が等しくなると4つの角が等しくなる。
菱形は4辺が等しい⇒平行四辺形の隣り合う辺が等しくなると4辺が等しくなる。
①…ウ、②…イ
(2)
対角線が垂直に交わる。
*正方形は4辺の長さが等しいほか、対角線の長さが等しく、かつ直交する。
長方形の対角線は長さが等しいが直交しない。
大問3(整数)
(1)
十の位がa、一の位がbの整数A。
A=10a+b
(2)
説明問題。
問題文を文字式に変換すると、
(10b+a)÷2=(10a+b)+1
19a-8b=-2 …①
(a+b)×3=(10a+b)-4
7a-2b=4 …②
①と②の連立を解くと、
a=2、b=5
A=25
大問4(図形の作図)
(1)
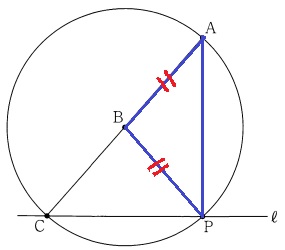
半径が等しいから、△ABPは二等辺三角形。
ア…B、イ…BA、ウ…BP
(2)①
半円の弧に対する円周角が90°であることから、
Aからℓに垂線をおろしても二等辺が作れるが、前の点Pと重なるので×!
先ほどはBA=BPを等辺とした二等辺三角形だったので、これ以外の等辺の組み合わせを考える。
AB=APだと、ABの長さよりA~ℓ間の距離のほうが遠いので、Pがℓ上にこない。
残りはPA=PBしかない。

PはA・Bから等距離にある→ABの垂直二等分線。
これとℓとの交点がP。
②
なぜ①の作図になるのか、理由を説明する。
『ABの垂直二等分線は2点A、Bからの距離が等しい点の集合だから』
PA=PBで△ABPは二等辺三角形であるといえる。
*点が集合して線になる。
大問5(数量変化)
(1)①
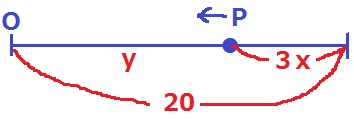
PがOを抜く前。
Pは毎秒3cmの速さだから、x秒後には3xcm移動している。
OP間の距離がy
y=20-3x
y=-3x+20
②
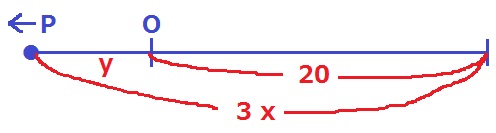
OがPを抜いた後。3xと20が逆転する。
y=3x-20
③
円の直径は20cm、Pの速さは毎秒3cmなので、
20÷3=20/3秒間
(2)
発想力が求められる。
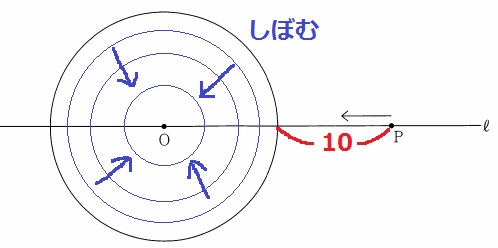
Pの出発と同時に円Oがしぼんでいく。
はじめはPが円Oを追っかける展開になる。
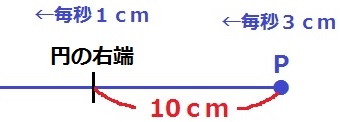
毎秒3cmのPが毎秒1cmの円の右端を追っかける。
1秒あたり、3-1=2cmずつ近づくので、
Pが円の右端と重なるのは、10÷2=5秒後
このときにPが円の周上にくるのでカウントが始まる。
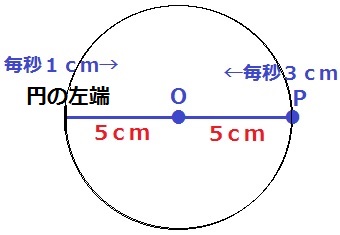
5秒後の様子。円の半径は5cmにしぼんでいる。
円の左端とPは10cm離れており、1秒あたり、1+3=4cmずつ近づく。
Pが円の左端と重なるのは、10÷4=5/2秒後
Pが円Oの周上または内部にある時間は5/2秒間
大問6(平面図形)
(1)
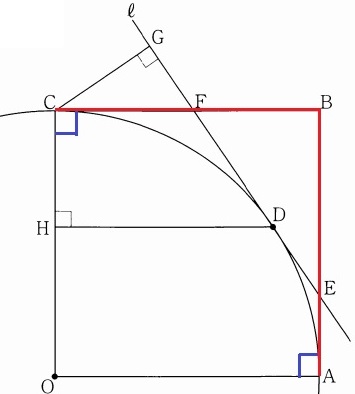
半径と接線は垂直に交わる。
正方形の内角より、∠OAB=∠OCB=90°なので、
円Oの接線は直線ABと直線BC。
ウ・エ
(2)
△CDG≡△CDHの証明。
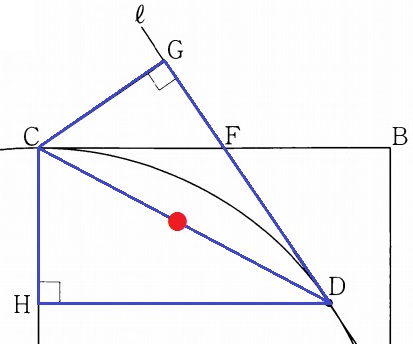
仮定より、∠CGD=∠CHD=90°
共通辺CD。
ここまではわかりやすい。
辺の情報が乏しいので、等しい1鋭角をさがす。
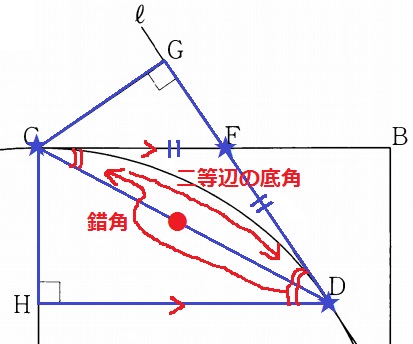
CF//HDより、錯角で∠CDH=∠DCF
点F、C、Dの位置関係に注目。
FC、FDは円Oの接線であり、C、Dが接点にあたる。
【円外の点から引いた2本の接線の長さは等しい】
FC=FD
△FCDは二等辺三角形だから、∠DCF=∠CDF
∠CDG=∠CDHとなり、斜辺と1鋭角が等しい直角三角形ゆえ合同。
(3)①
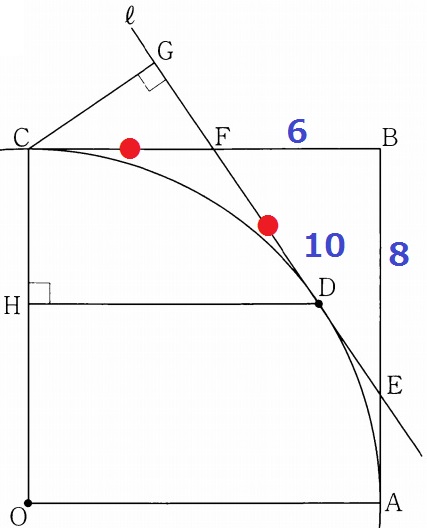
△BEFは辺の比が3:4:5の直角三角形→FE=10cm
前問の証明で用いた二等辺三角形FCDより、FC=FD(●)
…EDとEAも同じっぽい。
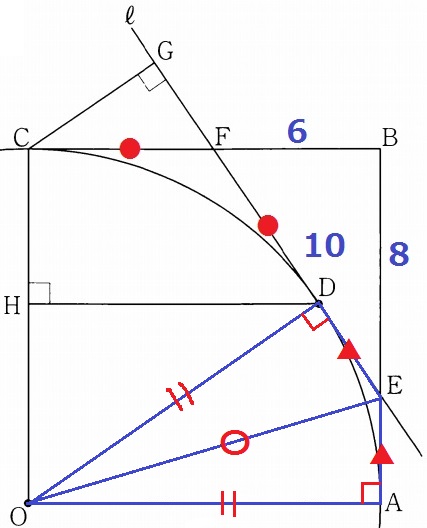
それらを1辺とする△EDOと△EAOに着目する。
半径でDO=AO、共通辺EO。
半径と接線は垂直だから∠EDO=∠EAO=90°
斜辺と他の1辺が等しい直角三角形なので、△EDO≡△EAO
対応する辺は等しいから、やはり、ED=EA(▲)
(*もしくは、先ほどのように接線の長さからED=EAを導ける)
FE=●+▲=10cm
CB+BA=(CF+FB)+(BE+EA)
=(●+6)+(8+▲)=24cm
正方形の2辺の和が24cmだから、1辺の長さは12cm。
②
△FEBと△ODHが∽っぽい。
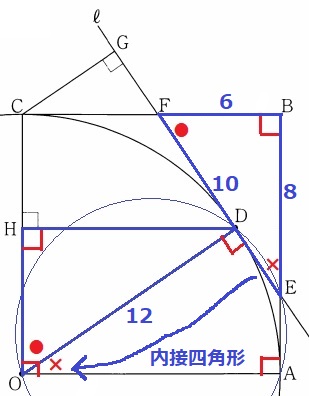
●+×=90°で角度を調査していく。
ここで、四角形DOAEに注目すると、∠EDO+∠EAO=180°
対角の和が180°だから、四角形DOAEは円に内接する四角形である。
そして、内接四角形の内角は、その対角の外角に等しい。
∠FEB=∠DOA=×
∠HOD=90-×=●
2角相等で、△FEB∽△ODH
相似比はFE:OD=10:12=5:6
面積比は相似比の2乗→△FEB:△ODH=25:36
△FEBの面積を36/25倍すればいい。
△ODHの面積は、8×6÷2×36/25=864/25cm2
@別解@
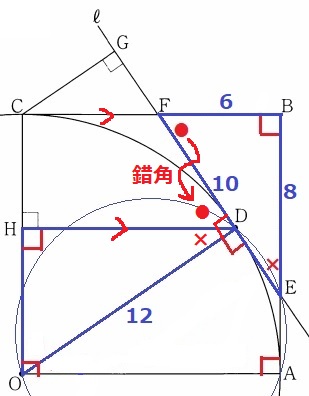
錯角のほうがわかりやすかったかもしれない。
∠ODH=90-●=×→2角相等→∽
●講評●
大問1
(9)文字を確認。x秒は時間、ymは距離。
距離÷時間=速さ。傾きである変化の割合は平均の速さ。
大問2
図形の性質を正確におさえる。ツメが甘いと間違える。
大問4
(2)①二等辺三角形はどこを等辺とするかで3パターンある。
大問5
設定がユニークであった。
直線ℓと交わる円周上の2点と中心Oだけを考えればいい。
(2)算数で解いてしまった。
大問6
(2)接線の長さは等しい。これを利用しないと面倒なことに。
(3)①等辺を図示しよう。
②相似っぽい⇒相似の証明。
直角がわかっているので、残りの1角を頑張って見つける。●+×=90°で調査。



コメント