平均12.4点(満点22点)
問題はこちら→東進ハイスクールさん(解答)
2019年愛知Aグループの解説は別ページ。
大問1(小問集合)
(1)
10-4÷(-2)
=10+2
=12
(2)
2/3÷(-4/3)2
=2/3×(9/16)
=3/8
(3)
√32-√8-√2
=4√2-2√2-√2
=√2
(4)
ハンカチ1枚をx円とおいて方程式。
3割引きは定価の7割。
2000-2x×0.7=880
x=800 →800円
(5)
-x+2=2x-7
x=3
y=-x+2に代入。
y=-3+2=-1
(3、-1)
(6)
8.2<√(n+1)<8.4
すべてを2乗する。
67.24<n+1<70.56
n+1=68、69、70
n=67、68、69
(7)
y変域が負なので、グラフは上に凸。
x=4のとき、y=-4となる。
-4=42a
16a=-4
a=-1/4
(8)
全体…5×4=20通り
a-b…(5、3)(4、2)(3、1)
3/20
(9)
弧AC(Bを含まない方)に対する中心角は
360-94=266°
∠ABC=266÷2=133°
大問2(小問集合2)
(1)
x=-3を代入。
(-3)2+(-3)a+15=0
-3a=-24
a=8
2x+a+b=0の式に、x=-3、a=8を代入。
-6+8+b=0
b=-2
(2)
a…最頻値(モード)は4
b…全体の冊数は30
中央値(メジアン)は15と16の平均→(4+5)÷2=4.5
c…悩みどころ:;(∩´_`∩);:
標本の数は30。平均値を□とすると、
〔合計÷30=□〕
平均値が+0.1大きくなったということは、
〔合計÷30=□+0.1〕となり、
〔合計〕は、30×0.1=3大きくなる。
条件から、範囲1~8と中央値4.5は変わらない。
4.5をまたいでしまうと中央値が変わってしまうので、
3大きくするには、〔1→4〕か〔5→8〕のいずれか。
〔1→4〕だと1冊がなくなくなり、範囲が変わってしまう。
〔5→8〕だから、Aが実際に借りた冊数は8冊となる。
(3)
傾きに注意しながら、どこの格子点が増えるかを調べる。
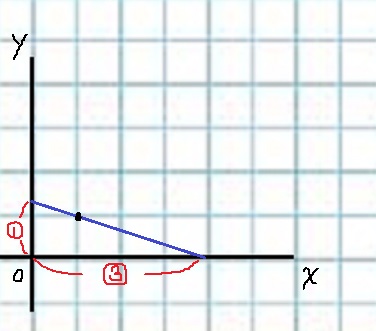
傾きは-1/3なので、原点0からの距離はx:y=3:1となる。
最初の格子点はココ。
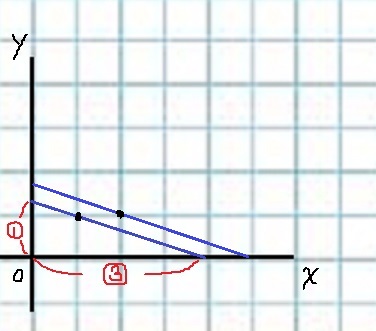
傾きを平行に維持しつつ、グラフを上にあげていくと、次の格子点は上のところ。
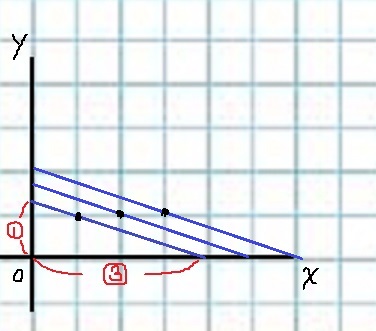
さらに上げると(1、3)の格子点とぶつかる。
これより上だと、三角形の中の格子点が3つになる。

切片bを調べる。
上限は(3、1)を通過するので、切片は(0、2)→bの最大値は2
下限は1:3を利用し、2×1/3+1=5/3
これより上でないと格子点が2つできない。
5/3<b≦2
(4)①
x軸は1マス10冊だが、y軸は5万であるのに注意!
30~60は1冊ごとに+5000円。
10冊で+5万なので、ちょうど右1マス上1マスとなる。
60~は1冊ごとに+2500。
先ほどの傾きの半分となり、右2マス上1マス。
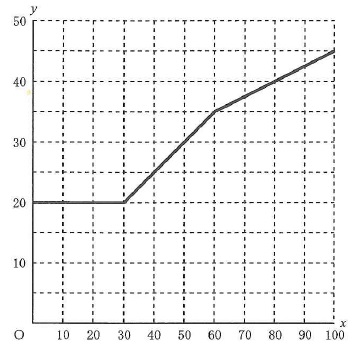
(2)
1冊5000円⇒10冊で5万
先ほどのグラフを拝借する。
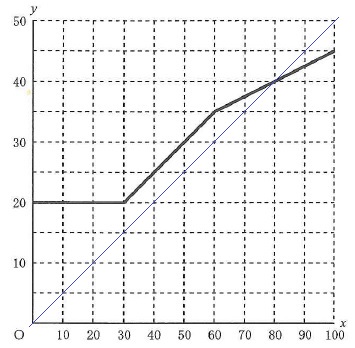
原点から45度線となる。
青線の以下にグラフがあれば、1冊あたり5000円以下となる。
交点から、80冊以上が正解。
大問3(図形)
(1)
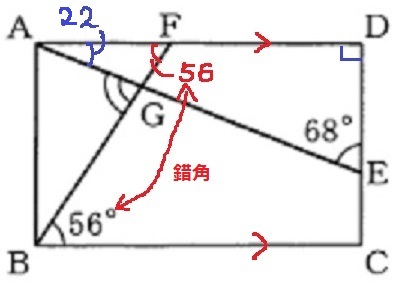
△AEDから、∠GAF=180-90-68=22°
AD//BCから錯角で、∠GFA=∠GBC=56°
△AGFで外角定理。
∠AGB=22+56=78°
(2)
BGは∠ABCの二等分線。
錯角で∠FBCを上にあげると、△DBGが二等辺とわかる。

AD:AB=DE:BC=2:8=1:4
AD:DB=1:3
DB=12×3/4=9
二等辺より、DG=9cm
②
前問のDG=9cmから、EG=9-2=7
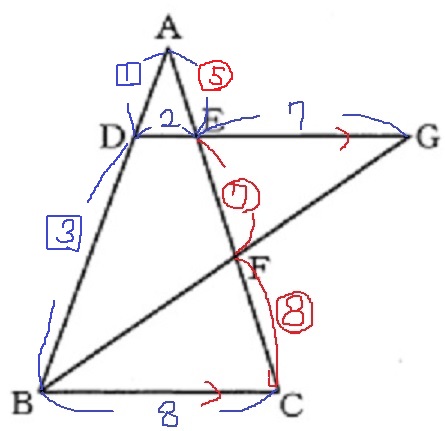
△EFG∽△CFB(2角が等しい)
EF:FC=7:8
AE:EC=AD:DB=1:3
AE=⑮×1/3=⑤
△ADEと△FBCにおいて、
AEとFCは一直線上にあり、DEとBCは平行。
三角形の面積比は〔底辺の比×高さの比〕で求められる。
△ADE:△FBC=AE×DE:FC×BC
=⑤×2:⑧×8
=10:64
=5:32
△FBCの面積は△ADEの面積の32/5倍
(3)①
AからBCに向けて垂線。
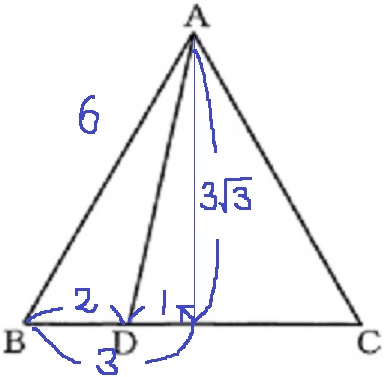
AD2=(3√3)2+12=28
AD=2√7cm
②
完成する立体は三角錐になる。
底面は△ADCで良いとして問題は高さ。
注意すべきはBDは面ADCに対して垂直な線にはならない!
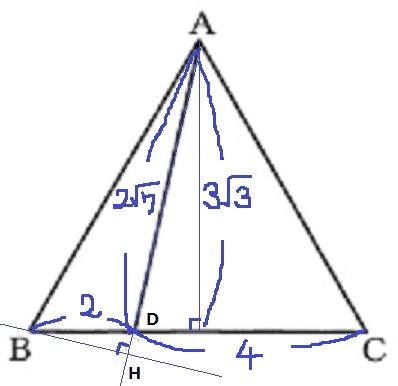
ADを延長。Bからひいた垂線との交点をHとおく。
BHが三角錐の高さになる。
BHは2つの三角形の相似を利用する。
BH=3√3×2/2√7=3√21/7
4×3√3÷2×3√21/7÷3=18√7/7cm3



コメント