2019年度　岡山県公立高校過去問【数学】解説

平均60.7点（前年比；＋2.9点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
－３－（－５）
＝－３＋５＝２

（２）
（－２）×６＝－12

（３）
２（ａ－２ｂ）－（ａ＋ｂ）
＝２ａ－４ｂ－ａ－ｂ
＝ａ－５ｂ

（４）
９ａ²ｂ÷３ａ
＝３ａｂ

（５）
（√３＋２）（√３－２）
＝√３²－２²＝－１

（６）
ｘ²＋３ｘ－１＝０
因数分解ができないので解の公式。
ｘ＝（－３±√13）/２

（７）
（１、１）⇒（３、－３）
右に２、下に４なので、傾きは－４/２＝－２
ｙ＝ａｘ＋ｂに代入して切片ｂを求める。
１＝－２×１＋ｂ
ｂ＝３
ｙ＝－２ｘ＋３

（８）
底辺が半径３ｃｍの円、高さ４ｃｍの円柱になる。
３×３×π×４＝36πｃｍ³

（９）
立方体なので、側面の６つの正方形は合同。
ＡＣは正方形ＡＢＣＤの対角線。
ＢＧは正方形ＢＦＧＣの対角線。
それぞれ合同な正方形の対角線だから、２本の対角線の長さは等しい。
ウ

（10）
50個のうち、印アリは５個。
印アリは全てで30個だから、30×50/５＝300個
イ

大問２（確率）

（１）
和が５の場合→（４、１）（１、４）（２、３）（３、２）
４通り

（２）①
Ｂに止まるにはＡから５進んだときと、
さらに１周して９進んだ時→９

②
和が５⇒４通り
和が９⇒４通り
計８通り
すべての出目の出方は６×６＝36通り
確率は８/36＝２/９

（３）①
それぞれの頂点に止まる出目の数は…
Ａは４・８・12
Ｂは１・５・９
Ｃは２・６・10
Ｄは３・７・11

岡山モノポリークラブより。
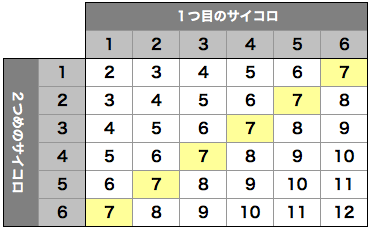
教科書のどこかに載っているはず。
１番多くあらわれるのは、対面の和である７。
次に６・８。次に５・９。
４・10、３・11、２・12と、和が７から遠ざかるにつれて出にくくなる。
最も止まりやすい頂点は、３・７・11のＤ。

②
上の表から、和が３と11はそれぞれ２通り。
和が７は６通りで計10通り。
確率は10/36＝５/18

大問３（平面図形）

（１）
ＢＣの垂直二等分線を描き、交点が点Ｅとなる。

（２）
△ＡＦＩと△ＤＦＪの合同を証明する。

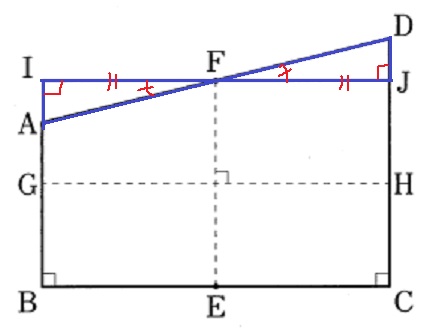
ＢＩ⊥ＢＣ、ＣＤ⊥ＢＣ、ＢＣ//ＩＪから、
∠ＡＩＦ＝∠ＤＪＦ＝90°
ＦはＡＤの中点なので、ＡＦ＝ＤＦ
これに対頂角を組み合わせ、直角三角形の合同条件の１つである、
斜辺と他の１鋭角が等しい点を指摘する。

（３）
ア：ＱＲ＋ＴＳ＝２ＶＵ

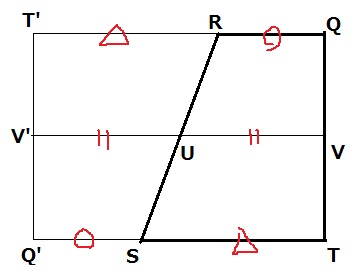
台形ＲＳＴＱをＵを回転の中心として点対称させる。
ＶＵの２倍はこの長方形の横の長さになり、ＲＱ（○）＋ＴＳ（△）と同じ。

イ：四角形ＱＲＳＴ＝ＱＴ×ＶＵ

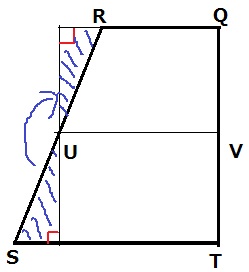
前問の証明問題と同じ考えを用いる。
合同の直角三角形を作成して移植すると長方形。
長方形の縦がＱＴ、横がＶＵなので等式が成り立つ。

ウ：五角形ＰＱＲＳＴ＝ＱＴ×ＰＸ
エ：五角形ＰＱＲＳＴ＝ＱＴ×ＷＵ
どちらかが間違っている。

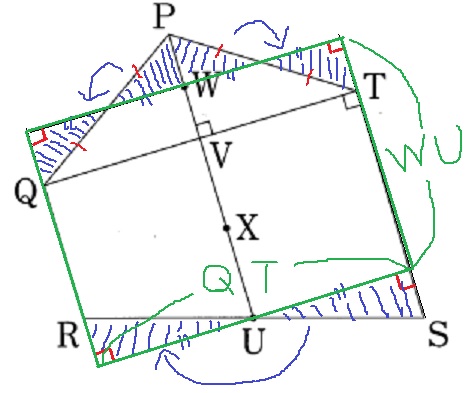
ウとエもＱＴはあるので、ＱＴを１辺とする長方形を考える。
補助線は辺の中点を通過させることを意識しよう。移植後の姿が↑の長方形。
よって、正しくないのはウ。

大問４（整数）

（１）
連続する３つの自然数の和が３の倍数になる理由。
教科書によく載っている証明で、おまけに誘導付き。
最も小さい自然数をｎとすると、他はｎ＋１、ｎ＋２と表せる。
ｎ＋（ｎ＋１）＋（ｎ＋２）
＝３ｎ＋３＝３（ｎ＋１）
ｎ＋１が自然数だから、３（ｎ＋１）は３の倍数。
よって、題意は満たされた。
①…ｎ＋２　②…ｎ＋１

（２）
ア：奇＋偶＋奇＝偶になるので×。
イ：偶＋奇＋偶＝奇になるので×。
ウ：先ほどの証明の結果にでた３（ｎ＋１）は、中央の自然数ｎ＋１を３倍している。○
エ：ｎ＋（ｎ＋２）＝２ｎ＋２＝２（ｎ＋１）。これは中央の自然数の２倍。○
ウ・エ

（３）
連続する３の自然数で、最も小さい数と最も大きい数の積に１を足すと、
中央の数の２乗になる理由。
日本語の部分は問題文に載っているので数式だけ書く。
ｎ（ｎ＋２）＋１＝ｎ²＋２ｎ＋１＝（ｎ＋１）²

（４）
前問にあてはめるだけ。
（ｎ＋１）²＝314
ｎ＋１＝18
ｎ＝17
最小の数が17だから、連続する３つの自然数は17・18・19となる。

大問５（数量変化）

（１）
固定された長方形に直角二等辺三角形が毎秒１ｃｍで突っ込む。
①②③
点ＣがＥＦ上にあるとき、ＥＦ＝４ｃｍだから０～４秒。
０≦ｔ≦４
①…４

毎秒１ｃｍの速さで動くので、ｔ秒後の動いた長さはｔｃｍ。

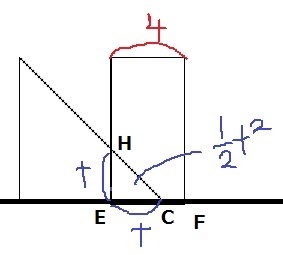
ＣＥ＝ＥＨ＝ｔｃｍ
Ｐ＝ｔ×ｔ×１/２＝１/２ｔ²ｃｍ²
②…ｔ、③１/２ｔ²

④⑤
２点Ｂ、ＣがＥＦ上にいないとき（４＜ｔ＜８）
すなわち、長方形の横ＥＦが直角二等辺三角形の辺ＢＣ上にあるとき。

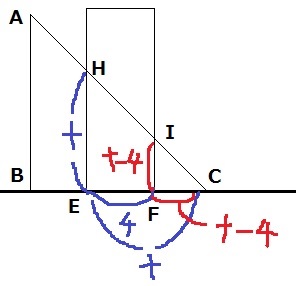
ＣがＥから動いた距離はｔｃｍ。
ＦＩ＝ＦＣ＝ｔ－４ｃｍ
Ｐは台形ＨＥＦＩの面積。
（ｔ＋ｔ－４）×４÷２＝４ｔ－８ｃｍ²
④…ｔ－４、⑤…４ｔ－８

（２）
ＢがＥＦ上にあるとき（８≦ｔ≦12）
Ｐは△ＡＢＣから△ＩＦＣをひけば良いらしい。

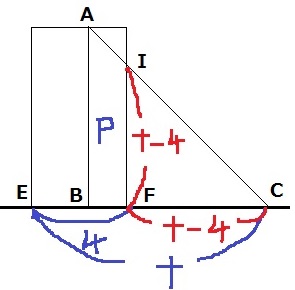
ＣＥ＝ｔｃｍ
ＣＦ＝ｔ－４ｃｍ
⑥…ｔ－４

⑦
過程を記述する。
Ｐ＝△ＡＢＣ－△ＩＦＣ＝８×８×１/２－（ｔ－４）²×１/２
＝32－（ｔ²－８ｔ＋16）/２
＝－１/２ｔ²＋４ｔ＋24ｃｍ²

（３）
いままでのおさらい。計算力も問われる。
①０≦ｔ≦４のとき、Ｐ＝１/２ｔ²ｃｍ²
②４＜ｔ＜８のとき、Ｐ＝４ｔ－８ｃｍ²
③８≦ｔ≦12のとき、Ｐ＝－１/２ｔ²＋４ｔ＋24ｃｍ²
Ｐ＝14を代入してｔを求め、ｔが該当範囲に収まるかを検証する。

①０≦ｔ≦４のとき
１/２ｔ²＝14
ｔ²＝28
ｔ＞０から、ｔ＝√28＝２√７
√４（２）＜√７→√７は２よりも大きい。
２√７は２×√７だから、その積は２×２＝４よりも大きくなる。
ｔが４より大きくなるので、０≦ｔ≦４の範囲にない。

②４＜ｔ＜８
４ｔ－８＝14
ｔ＝11/２
11/２を小数で表すと5.5なので、４＜ｔ＜８の条件を満たす。

③８≦ｔ≦12のとき
－１/２ｔ²＋４ｔ＋24＝14
－１/２ｔ²＋４ｔ＋10＝０
ｔ²－８ｔ－20＝（ｔ＋２）（ｔ－10）＝０
ｔ＝－２、10
８≦ｔ≦12から、ｔ＝10
したがって、ｔ＝11/２、10
公立高校入試解説ページに戻る