平均24.4点(前年比;-1.9点)
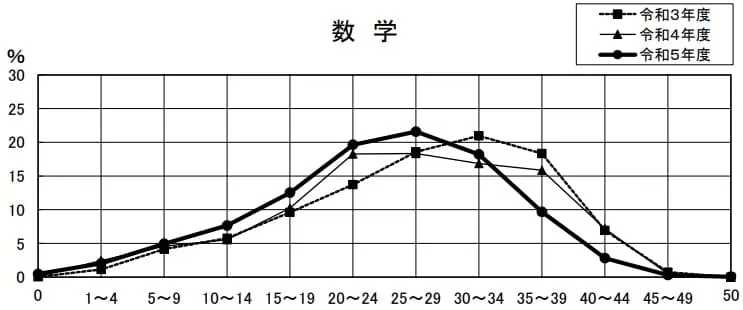
問題はこちら→奈良県教育委員会(解答用紙・正答表)
大問1(小問集合)-71.9%
(1)① 97.2%
7-(-6)
=7+6
=13
② 90.3%
15+(-4)2÷(-2)
=15+16÷(-2)
=15-8
=7
③ 86.8%
(x+2)(x-5)-2(x-1)
=x2-3x-10-2x+2
=x2-5x-8
④ 92.5%
√2×√6-√27
=2√3-3√3
=-√3
(2) 90.4%
x+4y=5 …①
4x+7y=-16 …②
①×4-②をすると、9y=36
y=4
①に代入、x+16=5
x=-11
x=-11、y=4
(3) 90.0%
x2+5x+1=0
解の公式を適用して、x=(-5±√21)/2
(4) 69.2%
a<0、b<0
引き算と掛け算、割り算はマイナスとマイナスがプラスに変わる。
足し算(a+b)が最も小さい値になる。
@@
適当な値を代入してもOK。
a=-1、b=-2とすると、
a+b=-1+(-2)=-3
a-b=-1-(-2)=1
ab=-1×(-2)=2
a/b=-1÷(-2)=1/2
(5) 64.0%
体積比は相似比の3乗。
A:B=23:33=8:27
Bの体積は、24×27/8=81cm3
(6) 79.3%
全体は、23=8通り
3回目で原点Oに戻るには、+1+1-2=0
表を2回、裏を1回出せば良い。
3回のうち裏をどの回で出すか→3通り
確率は3/8
(7) 62.9%
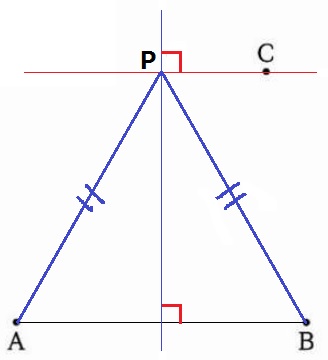
△PABはABを底辺とする二等辺三角形。
PはAとBから等距離にあるので(PA=PB)、PはABの垂直二等分線上にある。
また、AB//PCから同位角は90°で等しく、Cを通る垂線との交点がPとなる。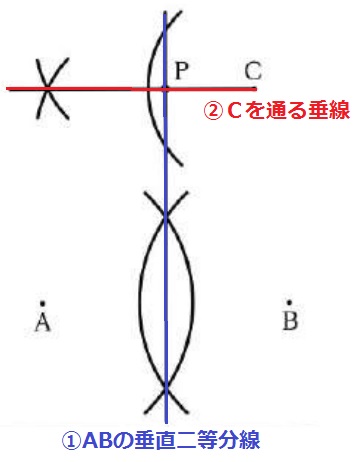
公式解答より。
(8) 28.9%!
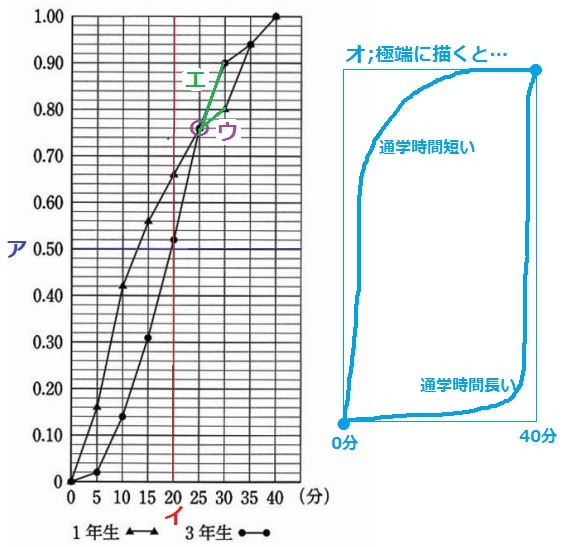
ア:中央値は累積相対度数が0.50のときの値。
1年生(▲)が3年生(●)より左にある→1年生の方が中央値は小さい。×
イ:20分未満の累積相対度数はいずれも0.50を超えているので、半分以上いる。〇
ウ:累積相対度数はあくまでも割合。1年生は75人、3年生は90人。
全体の人数(度数)が違えば、それぞれの76%の人数も異なる。×
エ:25分以上30分未満の相対度数=30分の累積相対度数-25分の累積相対度数
1年生の度数…75×4%、3年生の度数…90×14%だから、3年生の方が多い。〇
オ:累積相対度数が0.76で逆転するが、それまでは▲が左側に寄っている。
およそ3/4の割合で1年生の方が通学時間が短い。〇
イ・エ・オ
*誤答はア・ウもしくはイ・エが多かった。
大問2(平面図形)-30.6%
(1)① 54.9%

半径と接線は直交する。OP⊥XY、OQ⊥XZ
四角形XPOQの内角から、∠POQ=360-(90+90+45)=135°
*誤答例は105、120。
② 38.4%
△XPOと△XQOに着目すると、
∠OPX=∠OQX、OP=OQ(半径)、共通辺OXより、
斜辺と他の1辺が等しいから合同。
∠OXP=∠OXQだから、XRは∠YXZの二等分線である。
「辺」と「距離」を用いてXR上にある点を説明するので、
答えは『2辺XY、XZから距離が等しい点』
*誤答は、辺と辺との距離など。
③ 3.6%!!
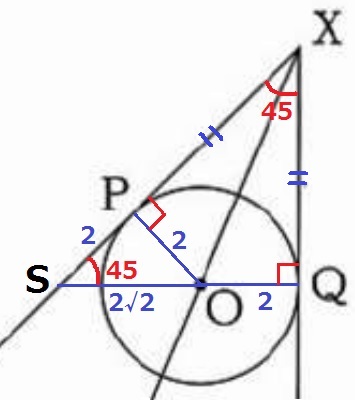
XPとQOの延長との交点をSとする。
△XSQの内角は45°―45°―90°だから直角二等辺三角形→∠PSO=45°
△PSOも同様に直角二等辺で辺の比は1:1:√2→SO=2√2cm
SQ=2+2√2cm
XQ=SQ=2+2√2cm
△XPO≡△XQOより、XP=XQ=2+2√2cm
*誤答例―2√3、4
(2)① 82.2%

∠BAD=90°と∠BXD=45°を、弧BDに対する中心角と円周角の関係で捉えると、
X・B・DはAを中心とする円Aの円周上にある。
半径より、XA=AB=AD
AXは正方形ABCDの1辺の長さに相当する。
イ
② 0.8%!!!
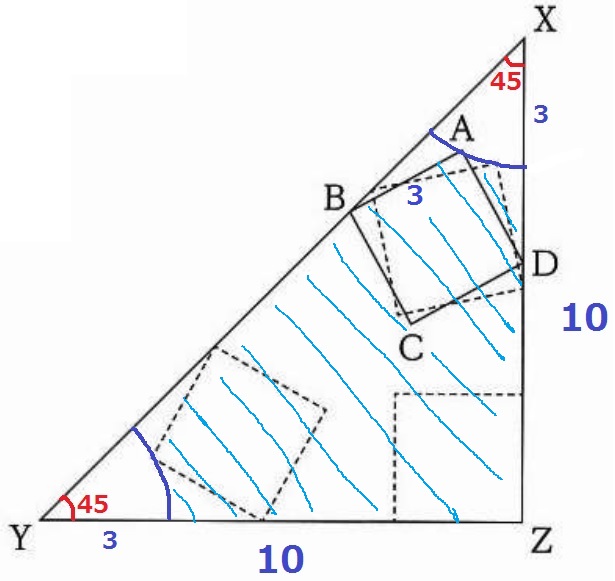
大事な情報はココ↓
『2点B、Dの位置が変わっても、2点X、Aの間の距離について同じことがいえる』
『同じこと』は前文の太郎のセリフ。
つまり、XAの長さはBとDが移動しても正方形ABCDの1辺の長さで変わらない。
正方形が通過できない端の部分は半径3cm、中心角45°の扇形となる。
Y側も同様で、通過できない部分を合わせると半径3cmの4分の1円なので、
通過できる部分の面積は、10×10÷2-3×3×π÷4
=50-9/4πcm2
*誤答例―7、6、41
大問3(関数)-46.7%
(1) 73.4%
y=-1/2x2について、
x=0のとき、最大値y=0
x=-4のとき、最小値y=-8
-8≦y≦0
(2) 76.3%
y=-1/2x2にそれぞれのx座標を代入する。
C(-4、-8)→D(2、-2)
右に6、上に6だから傾きは1。
Cから右に4、上に4移動して、切片は-8+4=-4
y=x-4
(3) 45.1%
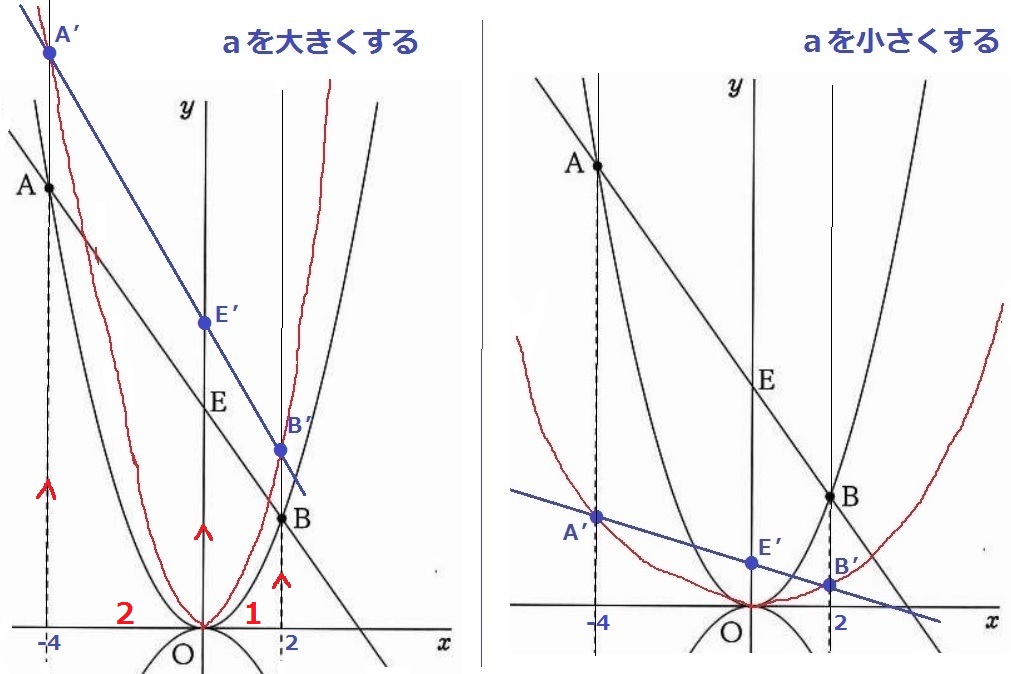
実際に描いてみる。
aを大きくすると、放物線の開きは小さくなる。
ア:ABの傾きは急になる→一次関数の傾きは小さくなる。〇
逆に、aを小さくするとABの傾きは緩やかになる。こちらの方が判断しやすいかもしれない。
イ:傾きが急→ABがより斜めになるので、ABは長くなる。×
ウ:Eの位置が上にあがるから、△OABの面積は増加する。×
エ:AE:EB=4:2=2:1で一定。×
x=-4、0、2の平行線に注目し、平行線と線分の比を使うと見えやすい。
ア
(4) 10.7%!
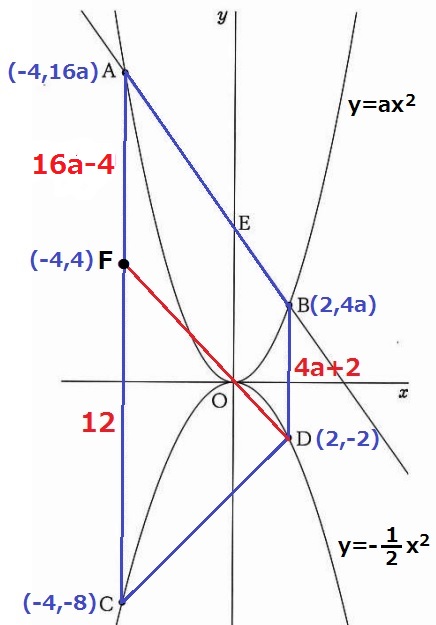
A(-4、16a)B(2、4a)
DOを延長、ACとの交点をFとする。
FDが四角形ACDBの二等分線になる。
Dから左に2、上に2でOだから、Oから左に4、上に4でF(-4、4)
FC=4-(-8)=12
AF=16a-4、BD=4a-(-2)=4a+2
四角形ACDBは台形なので、上底と下底の和が等しいと面積が等しくなる。
すなわち、AF+BD=FC
(16a-4)+(4a+2)=12
20a=14
a=7/10
*誤答例―1、1/2
大問4(平面図形2)-31.1%
(1) 60.3%
△AEF∽△BCEの証明。
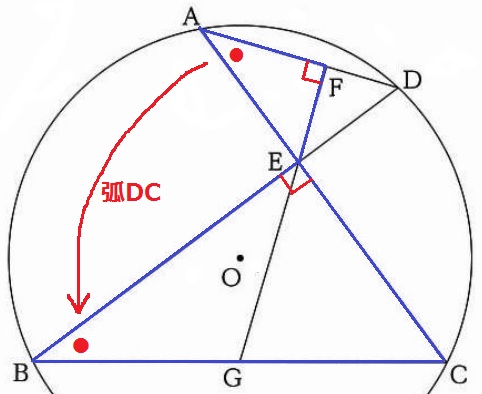
仮定から∠AFE=∠BEC=90°
弧DCに対する円周角で、∠EAF=∠CBE(●)
2角が等しいから∽。
(2) 43.0%
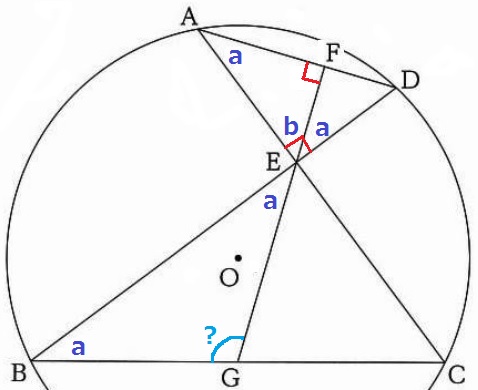
弧CDの円周角より、∠EBG=a
∠AEF=bとする。
△AEFの内角から、a+b=180-90=90°
∠AED=90°なので、∠FED=90-b=a
対頂角で、∠BEG=a
△BGEの内角で、∠BGE=180-2a°
*誤答例―180-a、90-a
(3)① 23.3%!
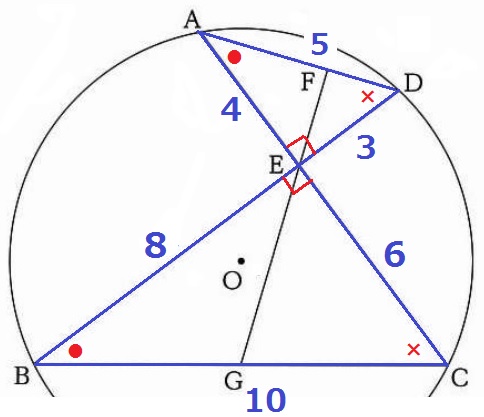
DE=3cm、AE=4cmから、△AEDは3:4:5の直角三角形。
対頂角や円周角から2角相等で△AED∽△BEC
△BECの辺の比も3:4:5→EC=6cm
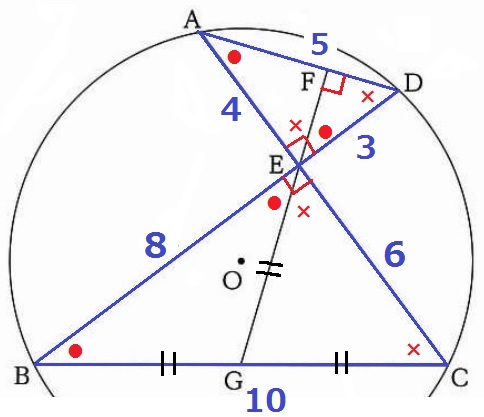
前問のa=●、b=×、●+×=90°として角度を調べると、
∠GEB=●、∠GEC=×
△GEBと△CEGは底角が等しい二等辺三角形。
BG=EG=CGより、GはBCの中点である。
△CEGの面積は△BCEの半分だから、8×6÷2÷2=12cm2
*誤答例―15、18、72/7
② 1.8%!!
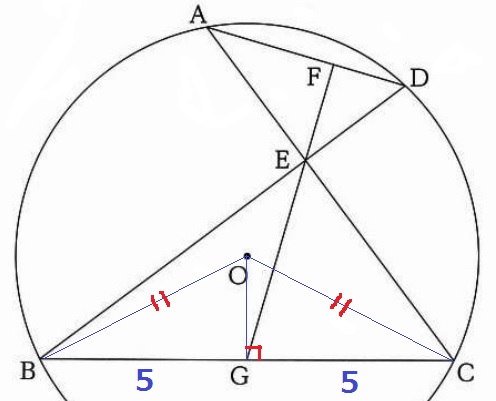
唐突に半径を求めさせられる(;´・ω・)
どの線分も中心Oを通らないので、半径を斜辺とする直角三角形で三平方を試みる。
半径OB=OC、△OBCは二等辺三角形。
頂角Oから底辺BCの中点Gに直線をひくと直交する。OG⊥BC
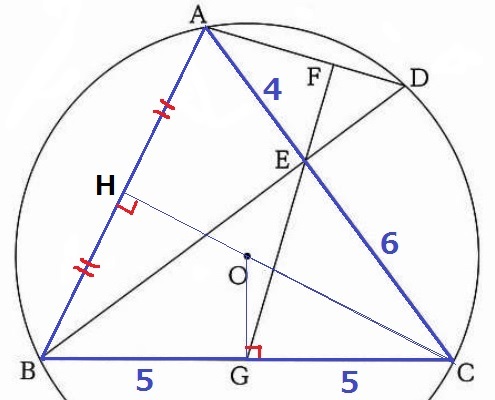
これだけでは情報が足りないので、広い視点でみてみる。
AC=BC=10cmに着目してABに補助線を描く。
ABの中点をHとすると、△ABCは二等辺三角形だから先と同様にCH⊥AB
また、中心OはABの垂直二等分線であるCH上にある。
(中心点の作図方法を思い出そう。OはAとBから等距離にある)
逆に言えば、COを延長するとHを通過することになる。
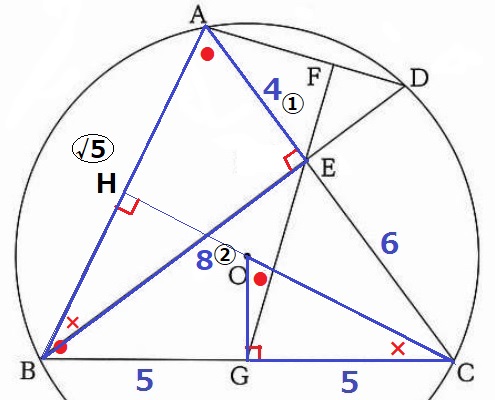
∠OCG=×、∠COG=●、●+×=90°で等角を記していく。
△BCHの内角で、∠HBC=●
二等辺ABCの底角で、∠CAB=●
∠AEB=90°だから、△AEBの内角は●―×―90°
2角相等より△OGC∽△AEB
AE:BE=4:8=①:②
△AEBの辺の比で三平方→AB=〇√5
AB:EB=OC:GC=〇√5:②
半径OC=5×〇√5/②=5√5/2cm
*誤答例―5√3/2、6
@余談@
思いっきり高校分野に入るので参考程度に載せておきます。
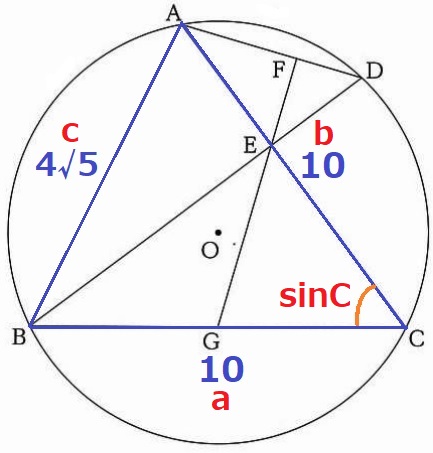
△ABCは円Oに内接している。
数Ⅰで習う正弦定理を使うと、外接円の半径Rを求めることができる。
正弦定理【c/sinC=2R】
△AEBで三平方→AB=4√5cm
余弦定理からcosC=(a2+b2-c2)/(2ab)=(100+100-80)/(2・10・10)=3/5
sin2C+cos2C=1より、sin2C=1-(3/5)2=16/25
sinC=4/5
正弦定理から外接円の半径R=c/(2sinC)=4√5/(2×4/5)=5√5/2cm
●講評●
大問1
(4)マイナスが変わらない選択肢を選ぶ。
(6)表と裏を何回出せば原点Oに戻るか。
(7)②がつまづきやすいか。90°の同位角がポイントになる。
(8)奈良以外の中学生も挑戦しておきたい問題。
社会科の資料問題みたいにいろんな角度からグラフを見る必要がある。
大問2
(1)②角の二等分線上の点はどのような点の集まりか。
具体的な辺を指摘して説明する。
③直角二等辺の辺の長さがわかっていない。
相似に頼れないので、等角をもとに図形の特徴を探し出す。
(2)①円周角が出てくるので、とりあえず円を描いてみる。
②『2点XAの距離について同じことがいえる』
問題文のヒントを取りこぼさないこと!
XAが変わらない→XAを半径とする扇形の弧上をAが動く。
大問3
(3)すべて選べではないのが幸い。
開きが小さくなるほど、A、E、Bが上にあがっていく。
エが判断しづらいかもしれない。平行線に注目する。
(4)台形の面積比は上底+下底の和の比。他県でもよく見かける。
ODを延長してACとの交点座標を調べる。
大問4
(2)都立でも似たような問題が出てくる。
a+b=90°、円周角、対頂角。いろいろ駆使してaを見つける。
(3)②前問のaをヒントに等角を調べていく。
すると、△BCEの中に2つの二等辺三角形があり、GがBCの中点とわかる。
②難所でした(;`ω´)
正弦定理を封じると三平方しかない。まずはOG⊥BCに気づく。
COの延長がABの中点を通るか。この理由も説明できるようにしたい。
等角を記して相似を用いる。



コメント