2011年度　千葉県公立高校入試【前期】数学解説

問題はコチラ→ＰＤＦファイル

大問１（計算）

(１)－１２÷４
＝－３

(２)４－３^２×(－２/３)　←累乗が先
＝４－９×(－２/３)　←掛け算割り算が先
＝４－(－６)　←符号ミス注意
＝４＋６
＝１０

(３)２(３ｘ－４ｙ)－５(ｘ－２ｙ)
＝６ｘ－８ｙ－５ｘ＋１０ｙ　←符号ミス注意
＝ｘ－２ｙ

(４)Ｓ＝３(a＋ｂ)/２をaについて解きなさい。
→　a＝～の形に置き換える。

両辺を２倍して右辺の分母を払う。
２Ｓ＝３(a＋b)
２Ｓ＝３a＋３b
aを左辺へ、a以外の要素を全て右辺へ移項
－３ａ＝－２Ｓ＋３b　　←両辺を÷（－３）
ａ＝(－２Ｓ＋３ｂ)÷(－３)＝２/３Ｓ－ｂ
(右辺の÷(－３)は、－２Ｓだけでなく＋３bについても割ります)

（５）(３－√７)^２
＝(３－√７)(３－√７)
＝９－２×３√７＋７
＝１６－６√７

(６)
解の公式。
ｘ＝(－５±√２５－８)/２＝(－５±√１７)/２

平方完成・・
このままでは左辺がうまく因数分解できない。
そこで、(ｘ＋○)^２=△の方式になるよう努める。
(ｘ＋５/２）^２－２５/４＋２＝０
(ｘ＋５/２)^２－１７/４＝０
(ｘ＋５/２)^２＝１７/４

ｘ＋５/２＝±√１７/√４
ｘ＝－５/２±√１７/２＝(－５±√１７)/２

大問２（小問集合）

（１）
一次方程式の一般式は、ｙ＝aｘ＋ｂ
xの値が１増加するときｙの値が３増加　→　変化の割合（傾き）aは３。
この時点でアイが消えます。
ｘ＝６のときｙ＝１２なので、ｘに６を代入。ｙの値が１２になるのはウ。

（２）
平行線２本を描き、錯角を利用。

∠ｘ＝３２＋４５＝７７°

（３）
立体図形の問題です。
回転体は、底面積が円になります。
本問では、下のようなコマみたいな形になります。

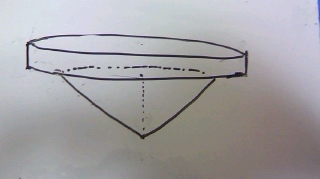
ゆがんでいますが、コマみたいな形になります。

上の円柱と下の三角錐にわけて考えます。

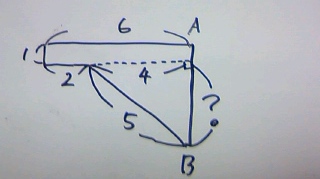
円柱は、底面が半径６cmの円で高さ１ｃｍ。
三角錐は、底面が半径４ｃｍの円。
高さは、三平方の定理３：４：５から３ｃｍであることがわかります。
よって、６×６×π×１＋４×４×π×３÷３
＝３６π＋１６π
＝５２πｃｍ³

（４）
確率ですから、(起こりうるパターン)/（全体のパターン）で答えがでます。

全体のパターンは箱A(３枚)→箱B(２枚)→箱A(残り２枚)ですから、３×２×２＝１２通り
起こりうるパターンは、場合分けをしながら分析していきます。
本問ではB箱から取り出す÷と－で場合わけし、値が１より大きくなる場合を探ります。

＠÷を取り出した場合＠
A箱から正の数と負の数を引き当てると必ず商に－が残ります。
また、(－1）÷（－３）＝１/３となり、題意を満たしません。
よって、(－３、－１)しかありません。

＠－を取り出した場合＠
(２、－１)　(２、－３)　(－１、－３)　の３通りです。

起こりうるパターンは全て４通り。
したがって、４/１２＝１/３　　答え　１/３

（５）
aは放物線の式ですから、放物線上のいずれかの点座標がわかればよいです。
そこで点Pに注目！
点Pは、直線ℓとｙ＝３/２ｘ＋５の交点ですから、
２本の直線の交点座標を求める方法が使えそうです。
つまり、直線ℓの式→直線ℓと、ｙ＝３/２ｘ＋５の交点座標Ｐ→ａ判明

直線ℓは、(０、１０)(１０、０)を通ります。
ｘの値が１０増えるとｙの値が１０減るので変化の割合は－１、切片は１０なので、
直線ℓの式は、ｙ＝－ｘ＋１０

ｙ＝－ｘ＋１０（直線ℓ）とｙ＝３/２ｘ＋５の交点Ｐは・・
－ｘ＋１０＝３/２ｘ＋５
ｘ＝２(点Ｐのｘ座標は２)

直線ℓのｘに２を代入
ｙ＝－２＋１０＝８(点Ｐのｙ座標は８)
よって、点Pの座標は(２、８)

ｙ＝aｘ² の式に戻ります。
ｘに２、ｙに８を代入。
８＝４a
a＝２　　　　答え、a＝２

（６）
恒例の作図問題。やや難です。
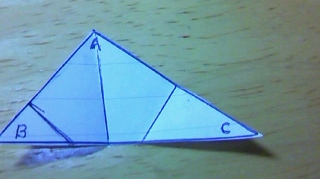
まず、辺ABを辺ACに向けて折ります。

本問では開かずにまた折るのですが、一度開けてみます。

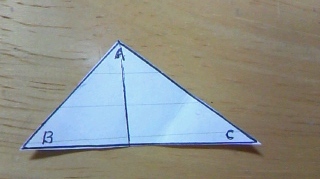
上のような直線をコンパスで正確に描くには、どうすれば良いのでしょうか。
折り目と辺BCとの交点をDとし、折り返し後にBが移動した点をB’とおきます。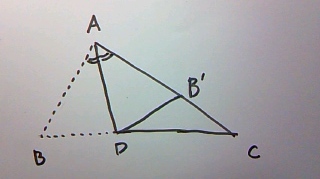
△AB’DはADを軸として△ABDを裏返してできた三角形ですから、(線対称)
△ABD　≡　△AB’D　(合同)
合同な三角形は対応する角も等しいので、
∠BAD＝∠B’AD
要するに、折り目である直線ADは、∠CABの二等分線です。
(角の二等分線の作図法は教科書参照)

もう一度、一回目の折り目からスタート。

ここから、点Aに向けて点Cを折り込みます。

(定規があるのは支え)

開くとこのような折り目が・・・

これも、先ほどと同様で、折り返した図形は合同であることを利用します。
２回目の折り目と辺BC上の交点をE、辺AC上の交点をFとします。

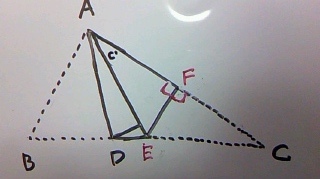
△AEF　≡　△CEF　となるので、AF＝CF
また、辺ACは一直線であり、∠AFE＝∠CFEですから、
∠AFEは∠CFEともに９０°

つまり、２回目の折り目EFは、辺ACの垂直二等分線ということがわかります。
(垂直二等分線の作図方法は教科書参照)

・・ここで、安心してはいけません。
２回目を折るときは紙を二重折りしているので、
折り目がADを軸に左側にも現れます。

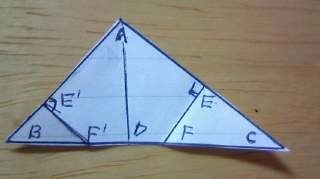
ADを対称軸とし、対称となる図形は左右の辺や角度がそれぞれ対応しますから、
AE＝AE’ 　∠AEF＝∠AE’F’＝９０°
コンパスでAEの長さをとって辺ABへ移し、その交点がE’です。
あとは、E’を通る辺ABとの垂線を描けば、３本目が完成します。
(垂線の作図方法も教科書参照)

大問３（文章題）

（１）
比の問題です。
比というのは、“比較の対象が違えば比べることができません”。
言い換えれば、“異なる比は同じように扱うことができません”。
本問でいえば、３：４と９：１６は異なる比なので、そのまま計算してはならないのです。

わかりやすいようにアナログの比を○、デジタルの比を△で囲むことで、
違う比であることを視覚的に表してみます。

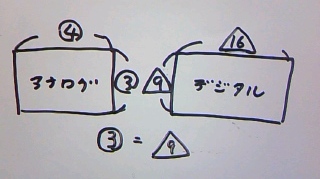
縦の長さは等しいので、○３＝△９であることがわかります。
つまり、○の中の数字を３倍すれば、○を△に置き換えることでき、
同じ比に置き換えることができます。同じ比であれば比較が可能です。

そこで、全てを△に統一します。

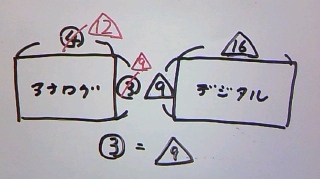
アナログとデジタルの面積比において、高さは共に△９で等しいので、
底面（横）の比がそのまま面積比となります。
長方形も三角形と同じで、高さを固定したら底面の長さの比が面積比になります。
アナログの面積：デジタルの面積＝１２：１６＝３：４
よって答えは、４/３倍

(＊注意・・・最後に３/４と答えるミスがあります！
アナログの何倍がデジタルであるかなので、もととなるアナログが分母にきます。
仮に３/４だと、１より小さい数ですからデジタルの方が小さくなってしまいますが、
本問の図１と図２を比較してわかるようにデジタルの方が広そうですよね)

（２）
とりあえず、文章通りの手順で解いてみます。
横の長さを１とする条件がついています。
○４＝１のとき、○３はいくつになるでしょうか？

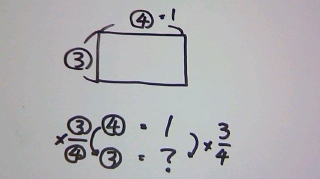
左辺の○４を○３にするには３/４倍すればよいので、右辺も３/４倍。
１×３/４＝３/４
①・・・３/４

長方形の面積は、縦×横なので、３/４×１＝３/４
②・・・３/４

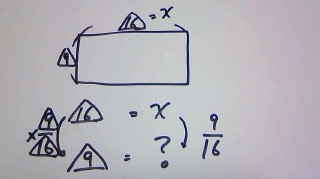
横の長さ△１６がｘなので、
縦の長さ△９は先ほどと同様に、
ｘ×９/１６＝　９/１６ｘ
③・・・９/１６x

同様に面積は、、
９/１６ｘ　×　ｘ＝９/１６ｘ²
④・・・９/１６ｘ²
まとめると、

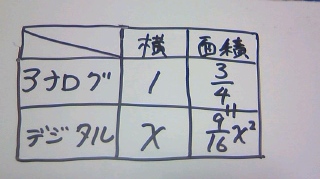
両者のテレビの面積が等しいことから、
９/１６ｘ²＝３/４
９ｘ²＝１２
ｘ²＝４/３
x＝√４/√３＝２/√３＝２/３・√３
つまり、デジタルテレビの横の長さが２/３・√３
よって、デジタルテレビの横の長さは、アナログテレビの横の長さの
２/３・√３÷１＝２/３ ・√３倍
⑤・・・２/３・√３

大問４（数量変化）

（１）
中学一年で習う比例式です。
原点から、(２，５)　(４，１０)　(６，１５)・・・と、ｘが２増えればｙが５増えているので、
変化の割合は５/２
よって、　ｙ＝５/２ｘ

（２）
問題文では「ある一箇所」と、水を入れ始めた場所が不明確なので、
ここから探りをいれます。
図４から、水入れ開始から０～２分間は、底面A上の水面の高さが０ｃｍであることから、底面A上から水を入れていないことがわかります。
残るは底面Aの右側か左側か、どちらから水を入れ始めたのでしょうか？

図２に戻り、１２分で高さ３０ｃｍ(＝満水)に達していますから、
直方体全体の体積は、２０×６０×３０＝３６０００ｃｍ³
１分あたり給水される水の体積は、３６０００ｃｍ³÷１２＝３０００(ｃｍ³/分)
１分間に３０００ｃｍ³の水を入れていることがわかります。

ここで、仮に底面Aの右側から水を入れ始めると、
右側の区切られた部分の体積は、２０×１０×１５＝３０００ｃｍ³なので、
１分で水浸しになります。
ということは、１分後には底面A上に水が流れ込みますから、
図４（２分間は水面０ｃｍ）と整合性が合いませんよね。
よって、底面Aの左側から水を入れ始めたことがわかります。

水が溜まる順番は、下の通り・・

＊溜まる手順が５つあるということは、
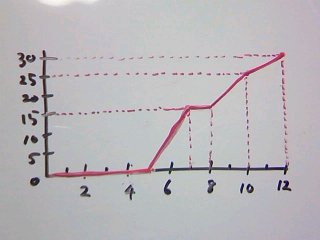
折れ線グラフでは４ヶ所折れるところがあるということですね。

あとは１箇所ずつ計算です。
①・・２０×３０×２５＝15000ｃｍ³　15000ｃｍ³÷3000(ｃｍ³/分)＝５分
→水入れ開始０～５分間は、底面A上に水がなく０ｃｍを維持。
②・・２０×２０×１５＝6000ｃｍ³  6000ｃｍ³÷3000(ｃｍ³/分)＝２分
→５分後に底面Aに水がなだれ込む。７分後にて②が満水。水面の高さは１５ｃｍに。
③・・２０×１０×１５＝3000ｃｍ³　3000ｃｍ³÷3000(ｃｍ³/分)＝１分
→７分後にはＡから右側に水がなだれ込みます。
８分後には満水に。この間、底面A上の水面の高さは変化しません。
④・・２０×３０×(２５－１５)＝6000ｃｍ³　6000ｃｍ³÷3000(ｃｍ³/分)＝２分
→底面積の拡大により、水面上昇率も緩やかに。開始１０分後で２５ｃｍに達する。
⑤・・水槽を満水にするのに１２分かかることは問題文から判明しているので、
グラフの線を(１２，３０)へ伸ばせばOK！
一応計算すると、２０×６０×(３０－２５)＝6000ｃｍ³
6000ｃｍ³÷3000(ｃｍ³/分)＝２分
１２分後にMAX３０ｃｍに到達することが、計算により確認されました。
かなり大雑把ですが、解答としては下のような感じです。

大問５（平面図形）

（１）
証明の出だしの部分が記載されているので、とりあえず誘導に従います。

∠ＦＤＣ＝∠ＦＥＣ＝９０°ならば
４点Ｅ、Ｆ、Ｄ、Ｃは直径をＦＣとする円の円周上にある。
まず、これは理解できますか？
試しに、点Ｅ、Ｆ、Ｄ、Ｃを円で囲ってみると、
円周角の問題であることが顕著に表れます。
円周角は中心角の半分ですので、円周角が９０°ならば中心角は１８０°。
つまり、その弦は一直線となり、円の直径にあたります。

円周角定理の逆です。
典型的な円周角の問題は、あらかじめ円が描かれて、点が円周上にありますが、
三角形の１つの角度が９０°であるとき、それと向かい合う辺を直径とする円を描いてみると、３点が同一円周上にきます（円周角が９０°なのは、中心角が１８０°で一直線だから）
これは円周角が中心角の半分である関係と同視でき、
各々の点は同一円周上にあることになります。

P⇒Qが真でも、Q⇒P、すなわち 逆は必ずしも真とは限らないのですが、
円周角定理の逆は真なのです。
円周角法理の逆は、”おのおの点が円周上にある”が結論になりますので、
最初はイメージがつかみにくいと思いますが、慣れておきましょう。
(ちなみに、同じ弧に対する円周角はどこも等しいという定理の逆も真で、結論は↑と同じ)

∠ＦＤＣと∠ＦＥＣは直角で、その弦ＦＣは一直線なので、
円周角が中心角の半分である関係と同視できます。
∠ＦＤＣと∠ＦＥＣは、ＦＣを直径とする円の円周上の角(＝円周角)で、
点Ｅ,、Ｆ、Ｄ、Ｃは同一円周上にあることがわかります。
(*言い換えると、直角三角形で直角をなす頂点は、
常に斜辺を直径とする円の円周上にあるわけですね)

∠ＦＣＥは弧ＦＥに対する円周角ですから、円周角の定理から
同じ弧ＦＥに対する円周角である∠ＦＤＥと同じ角度になります。
∠ＦＣＥ＝∠ＦＤＥ
よって、aの答えは、イ。

ｂも、ａと考え方は同様です。
試しに、直径をＡＢとする円を描くと・・

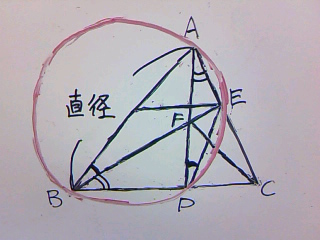
∠ＡＤＢ＝∠ＡＥＢ＝９０°ですから、直径をABとすると２つの角は円周角となり、
円周角が等しいということは、Ａ、Ｂ、Ｄ、Ｅはこの円の円周上にあるということになります。
よって、ｂの答えは、Ａ、Ｂ、Ｄ、Ｅ。

ｃです。
△ＧＢＥ∽△ＦＣＡを証明したいので、”どの相似条件が使えるか“を先に考えます。
問題文からは辺の長さが一切与えられていませんし、二等辺三角形や正三角形も見当たりませんよね。ということは、全ての辺の長さがわからない以上は角度から攻めていくしかないということになります。つまり、２角が等しいことを示せば、相似であることを証明できます。

そして、これまでの流れから察するに円周角の定理を用います。
また、ＧＥとＢＣの関係が平行であることから、錯覚や同位角も考えられますね。
△ＧＢＥと△ＦＣＡの各々の角に注目しつつ、等しい角度に印をしていきましょう。

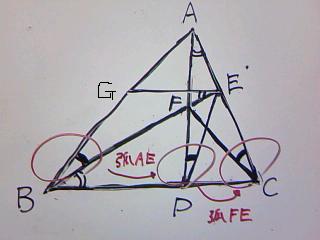
aより、点Ｅ、Ｆ、Ｄ、Ｃも同一円周上にあることから、
弧ＦＥに着目して、∠ＦＤＥ＝∠ＦＣＥ
ｂより点Ａ、Ｂ、Ｄ、Ｅは同一円周上にあります。
弧ＡＥに着目し、同じ弧に対する円周角は等しいことから、
∠ＡＢＥ＝∠ＡＤＥ

求めたいのは△ＧＢＥ∽△ＦＣＡなので、これらの三角形にあう角度に言い換えます。
∠ＡＤＥと∠ＦＤＥは同一の角ですから、
∠ＡＢＥ＝∠ＦＣＥ
∠ＡＢＥと∠ＧＢＥも同一の角ですから、
∠ＧＢＥ＝∠ＦＣＥ

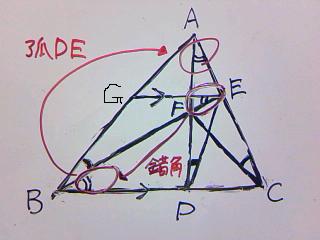
ＧＥとＢＣが平行であることから、錯角により、
∠ＧＥＢ＝∠ＤＢＥ
ｂより点Ａ、Ｂ、Ｄ、Ｅが同一円周上にあることから弧ＤＥに着目し、
∠ＤＢＥ＝∠ＤＡＥ
よって、∠ＧＥＢ＝∠ＤＡＥ

∠ＤＡＥと∠ＦＡＣは同一の角ですから、
∠ＧＥＢ＝∠ＦＡＣ

以上より、△ＧＢＥと△ＦＣＡにおいて、対応する２角が等しいから、
△ＧＢＥ∽△ＦＣＡ

（２）
相似関係にある図形の面積比は辺の長さの比の２乗で求まります。
つまり辺の長さがわかれば答えがでます。

では、どの辺の長さを求めるべきでしょうか？
△ＧＥＢと△ＦＣＡにおいて、判明している辺の長さは、AC＝５ｃｍのみです。
ということは、辺ACに対応する辺BEの長さがわかれば面積比がでるかもしれません。
そこで辺BEの長さを求めます。

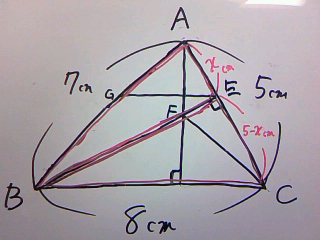
ポイントは、三平方の定理と方程式です。
辺BEは、直角三角形ABEとCBEの辺を構成していることに注目！

BEを求めたいのでBEをxとおきたいところですが、
それだと等式が作れないので、とりあえずAEをｘcmとおきます。
△ＡＢＥにおいて、三平方定理から、
BE²＝７²－ｘ²＝４９－ｘ²　・・・Ａ
△ＣＢＥにおいて、同様に、
BE²＝８²－(５－ｘ)²＝６４－(２５－１０ｘ＋ｘ²)
＝－ｘ²＋１０ｘ＋３９　・・・Ｂ

Ａ、Ｂはともに左辺がBE²で等しいので、右辺の値も一緒。
４９－ｘ²＝－ｘ²＋１０ｘ＋３９
１０ｘ＝１０
ｘ＝１
AEの長さは１ｃｍ。
△ＡＢＥにおいて、三平方定理から、
BE^2＝７²－１² ＝４９－１＝４８
BE＝±４√３
BE＞０より(長さは負の数にならない)
BE＝４√３
△ＡＥＢと△ＦＣＡにおいて、ＢＥ＝４√３　ＡＣ＝５ですから、
辺の長さの比が　　 ４√３：５
よって面積比は　４√３²：５² ＝４８：２５
答え、４８：２５
公立高校入試解説ページに戻る