2019年度　群馬県公立高校過去問【数学】解説

平均44.5点

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
①－４×３＝－１２
②６ａ²×１/２ａ＝３ａ³
③（ｘ＋ｙ）/２＋（ｘ－ｙ）/４
＝{２（ｘ＋ｙ）＋（ｘ－ｙ）}/４
＝（３ｘ＋ｙ）/４

（２）
２＜√ａ＜３を満たす自然数ａと求める。
根号が邪魔なので、すべて２乗。
４＜ａ＜９
ａ＝５、６、７、８

（３）
ｘ²＋５ｘ－６
＝（ｘ＋６）（ｘ－１）

（４）
式を整理してから代入。
（－ａｂ）³÷ａｂ²
＝－ａ³ｂ³÷ａｂ²
＝－ａ²ｂ
＝－３²×（－４）＝３６

（５）
ｘ²＝６ｘ
ｘ²－６ｘ＝０
ｘ（ｘ－６）＝０　←共通因数はｘ
ｘ＝０、６

（６）
中心角は円周角の２倍→４０°
蝶々型の２角の和は一緒（対頂角は相殺できるから）
４０＋ｘ＝２０＋５０
ｘ＝３０°

（７）
硬貨を４枚投げる。
すべての通り→２⁴＝１６通り
４枚投げたうち、２枚が表になる組み合わせ。
_４Ｃ_２→６通り
６/１６＝３/８

（８）
円柱の表面積＝底面積×２＋側面積
３×３×π×２＋３×２×π×４
＝１８π＋２４π＝４２πｃｍ²

（９）

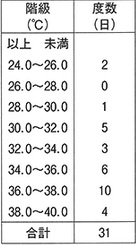
グンマー熱いね！
ア：37.0℃が５日あったかはわからない。×
37.9℃が10日あったかもしれない。
イ：統計は40.0℃未満しかないので判断に迷った人もいたかもしれないが、
40℃以上の日がなかったからこそ、統計がないと考えられる。〇
ウ：28.0-30.0の度数が１。×
相対度数は１/３１＝0.032…≒0.03
エ：（31＋１）÷２＝１６番目がメジアン。
上からいった方が早いかな？
上から１６番目は34.0-36.0の階級にある。〇

大問２（平面図形１）

（１）
角の二等分線を２本作図する。

（２）

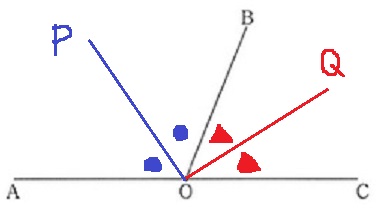
①一直線を半分にするので、∠ＰＯＱ＝９０°
②これを∠ＡＯＢ＝∠ａ、∠ＢＯＣ＝∠ｂとおいて説明する。

大問３（文章題）

一次方程式の記述問題。
貯金の回数がわかっていないので、
これをｘとおき、重さで等式を作る。
100円は３枚で、4.8×３ｇ
500円は１枚で7ｇ
（4.8×３＋７）ｘ＋250＝571
ｘ＝１５
貯金額を求める。
（100×3＋500）×15＝12000円

大問４（平面図形２）

（１）
△ＥＡＣが二等辺→底角が等しい

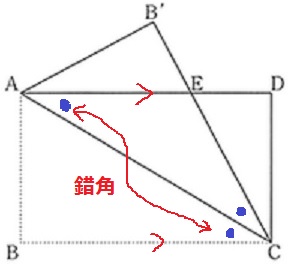
折り返しで同じ。錯角で上げる。

＠別解＠
△ＥＡＣが二等辺→ＥＡ＝ＥＣ
→△ＡＥＢ’≡△ＣＥＤを指摘してもいい。

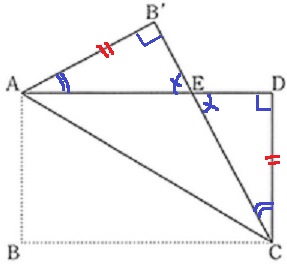
直角と対頂角で残りの角が等しい。
一辺両端角→合同

（２）
ＡＥをｘとおくと、ＥＤ＝１０－ｘ

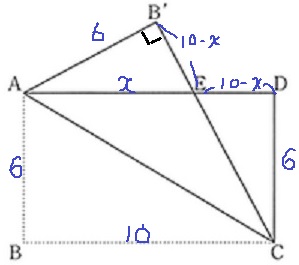
△ＡＥＢ’≡△ＣＥＤから、ＥＢ’=１０－ｘ
△ＡＥＢ’で三平方。
ｘ²＝（１０－ｘ）²＋６²
ｘ²－１００－２０ｘ－ｘ²－３６＝０
２０ｘ＝１３６
ｘ＝３４/５　ＡＥ＝３４/５cm

大問５（数量変化）

（１）
重なる部分の形が変わるところが転換点。

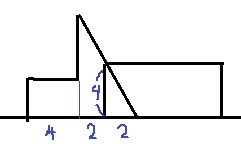
０～２秒後は直角三角形。ア…２

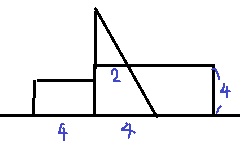
２～４秒が台形。イ…４
以降、台形＋長方形。

面積判定は慎重に！

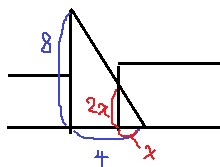
０～２秒後の面積判定。
横：縦＝１：２から、直角三角形の面積が出せる。
ｙ＝ｘ×２ｘ÷２＝ｘ²
あ…ｙ＝ｘ²

２～４秒後の面積判定。
長方形から青い直角三角形を控除する。
ｙ＝４ｘ－２×４÷２＝４ｘ－４
い…ｙ＝４ｘ－４

４～８秒後の面積判定。
右の台形が、（２＋４）×４÷２＝１２
左の長方形が３（ｘ－４）＝３ｘ－１２
ｙ＝３ｘ－１２＋１２＝３ｘ
う…ｙ＝３ｘ

（２）
Ｐの面積は、３×４＋４×８÷２＝２８ｃｍ²
重なる部分が２８÷２＝１４ｃｍ²はいつか？

ｘ＝４秒のとき、右側に１２ｃｍ²の台形があったので、
４～８秒のときになる。
ｙ＝３ｘのｙに１４を代入。
３ｘ＝１４
ｘ＝１４/３　１４/３秒後

大問６（平面図形３）

（１）
連立方程式を利用する説明記述。
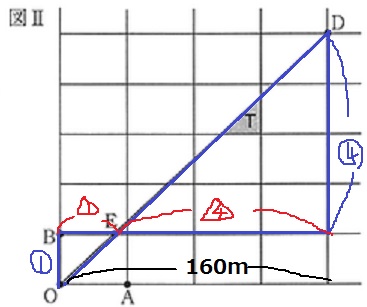
ＯＡ（横）をｘ、ＯＢ（縦）をｙとする。
〔Ｏ→Ｃ〕は横３本、縦２本
〔Ｃ→Ｄ〕は横１本、縦３本
３ｘ＋２ｙ＝１８０
ｘ＋３ｙ＝１３０
これを解いて、ｘ＝40、ｙ＝30
ＯＡ＝４０ｍ、ＯＢ＝３０ｍ

（２）①

ＢＥ＝１６０×１/５＝３２ｍ

②

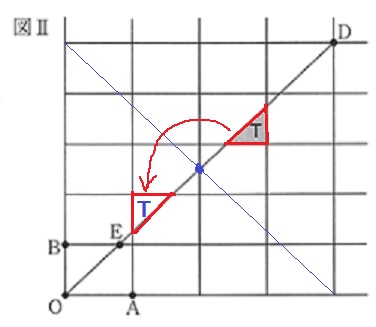
点対称の要領でＴを移転。

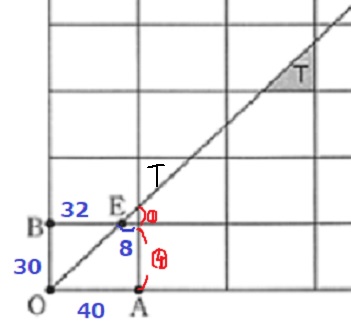
８と４０のところで∽。
３０＝④なので、①＝３０×１/４＝7.5

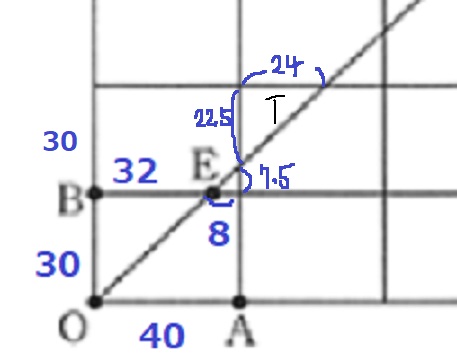
更に拡大。３０－7.5＝22.5
８：7.5＝□：22.5
□＝２４
Ｔ＝22.5×２４÷２＝２７０ｃｍ²

＠別解＠

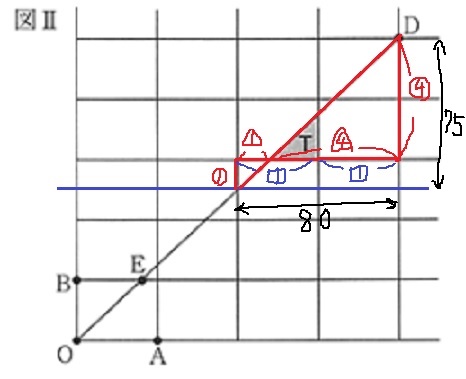
右上の長方形は、大きな長方形の４分の１。
辺の比が１：４の三角形がある。

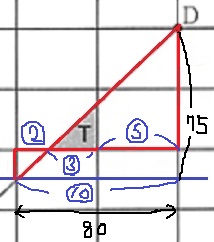
比を統合すると、２：３：５。
大きい三角形〔80×75÷２〕とＴの三角形の面積比は、
⑩²：③²になる。
Ｔ＝８０×７５÷２×９/１００
＝２７０ｃｍ²
公立高校入試解説ページに戻る