平均58.8点(前年比;+0.9点)
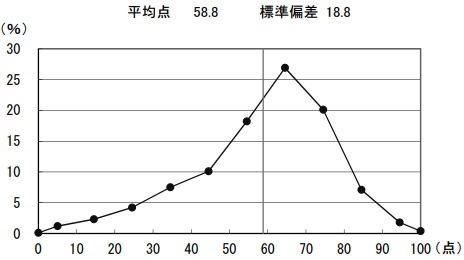
問題はこちら→リセマムさん
大問1(計算)-91.0%
(1) 98.3%
-5+(-4)
=-5-4
=-9
(2) 96.4%
(-4)2 -8×3/2
=16-12
=4
(3) 84.8%
(2x+y)/3+(x-y)/2
=(4x+2y+3x-3y)/6 ←全てを6で通分
=(7x-y)/6
(4) 92.8%
6/√2+√8
=3√2+2√2 ←有理化
=5√2
(5) 85.2%
七角形の内角の和を求める。
n角形の内角の和→180(n-2)
180×(7-2)=900°
(6) 88.3%
x2 -5x-6
=(x-6)(x+1)
大問2(小問集合)-57.9%
(1) 80.4%
平均値…(0×2+1×3+2×2+3×5+4×6+5×2)÷20=56÷20=2.8回
最頻値は度数の多い階級値→4回 よって、ア
(2) 58.8%
高さを三平方で求める。1:2:√3の直角三角形だから、高さは3√3cm
3×3×π×3√3÷3=9√3cm3
(3) 70.4%
下に凸のグラフを書いてみると、yの最小値はx=0のとき!
x=0のとき、最小値:y=0
x=-4のとき、最大値:y=8
0≦y≦8
(4) 71.8%
Bに止まるパターンと、Eに止まるパターンを足せば良い。
B:和が1はない。和が9→(3、6)(6、3)(4、5)(5、4)
E:和が4→(1、3)(3、1)(2、2) 和が12→(6、6)
計8通り
8/36=2/9
(5) 8.2%!!
今年の千葉は後期も容赦なかった((;゚д゚))
∠APB=30°、∠APC=90°となる点Pを描きたい。
点Pは△ABC上にくるわけでもないので、△ABCにこだわらない方が良い。
ポイントは円周角の定理
そこに気がつけても、もう少し思考を巡らせないと正解にたどりつけない。
∠APB=30°の作図
円周角の定理を使えば、点Pの候補地を円周で表せる。
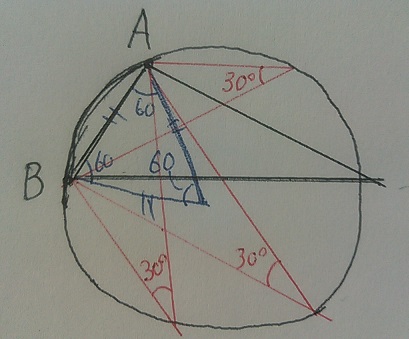
↑中心角を60°に設定すれば、円周角は一定なのでどこも30°
AとBを通る円の中心は、ABを1辺とする正三角形の残りの頂点である。

↑ 正六角形の頂点と円の中心は同じ
次に∠APC=90°の作図
同様に円周角定理を用いて、点Pの候補地を円周で描く。

半円の弧に対する円周角は直角であることを利用する。
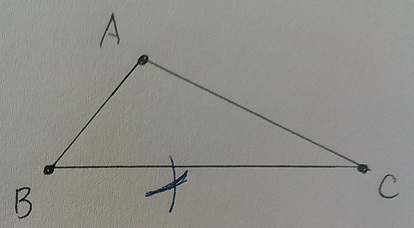
ABを1辺とする正三角形。
ABの長さをとり、AとBから印をつける。
交点はAとBを通る円の中心点。
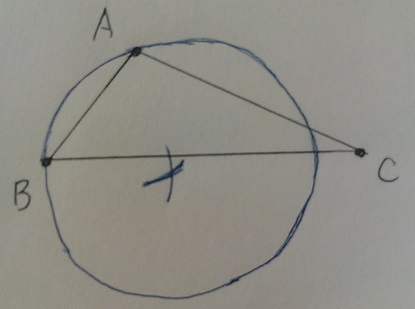
クルッ(雑)
このどこかに点Pがある。
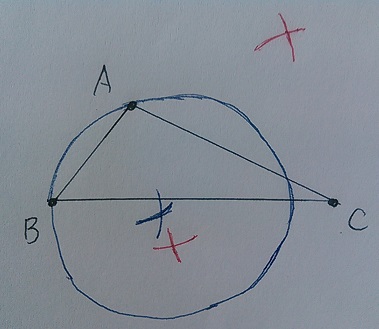
次に、ACの垂直二等分線。
ACを直径とする円の中心点はACの中点だから。
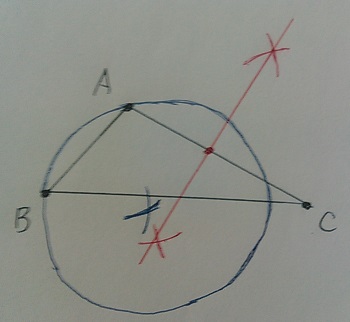
交点を中心に円を書くと・・
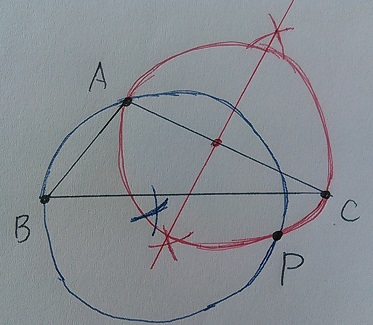
こうなる。
青い円のどこかと、赤い円のどこかに点Pがあるので、
青い円と赤い円の交点が点Pとなる。
△ABCばかりに目がいってると、なかなか思いつけない。
大問3(関数)-57.5%
(1) 87.5%
AとBはy軸を対称の軸として左右対称だから、Bのx座標は3
B(3、9)
(2) 70.7%
P(1、1) A(-3、9)
あとはこれを通る直線の式を求めるだけ。
右に4いって下に8だから傾き-2
1=-2×1+b b=3
y=-2x+3
(3) 14.4%!
△AOBと△PABは底辺がABで共通→高さが4:3

点Pとy軸との距離は、9×1/4=9/4
P(3/2、9/4)
A(-3、9)とPを通る直線の式を求める。
連立方程式
9=-3a+b
9/4=3/2a+b
a=-3/2、 b=9/2
y=-3/2x+9/2
y=0のとき、x=3
(3、0)
後期は試験時間が40分しかないので、迅速な計算力が求められる。
@別解@
連立がヤダ!という人は相似。

Pを通る垂線でABとの交点をQ、x軸との交点をR、
APを延長してx軸との交点(求める座標の点)をSとする。
△APQ∽△SPR
AQ=3+3/2=9/2
相似からRS=9/2×1/3=3/2
Sのx座標は3/2+3/2=3となる。
大問4(平面図形)-51.7%
(1)
はじめは合同の証明。△ABRと△ADRを刮目する。
正方形の1辺 AB=AD → a:イ 87.1%
共通辺で AR=AR
直角二等辺から∠BAR=∠DAR=45° →b:オ 94.0%
2辺夾角(間の角)が等しいので合同。
c:続いて、△PRB∽△BRQの証明。 6点―19.9% 3点―6.9% 無答―44.4%
共通角∠BRPがあるので、もう1つの角が等しいことを指摘すれば良い。 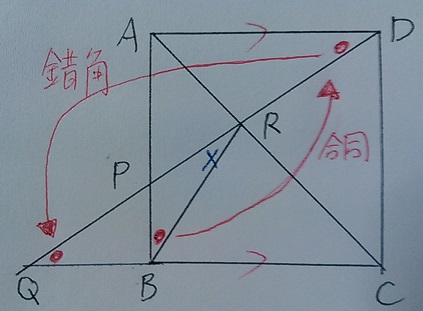
前問の合同関係を用いる。
∠RBP=∠RDA
AD//QCから錯角で∠RDA=∠RAB
したがって、∠RBP=∠RABで2角が等しいとわかる。
筋道が立てやすいので正解したいところ。
(2) 5.7%!!
BRは△PRBの1辺なので、前問の相似が利用できそう。
とりあえず、長さのわかる辺を調べていく。
AP:PB=2:1から、AP=4cm、PB=2cm
△APD:△BPQ=AP:BP=4:2=2:1
QB=3cm
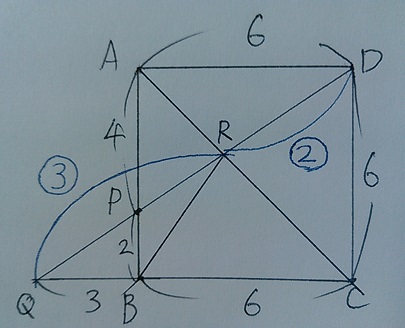
これで、△PRB:△BRQ=PB:BQ=2:3とわかった。
あとはBRに対応するQRがわかれば嬉しい。
△DQCで三平方。
DQ=√(62+92)=√117=3√13
△ARD:△CRQ=AD:CQ=6:9=2:3
QR=3√13×3/5=9/5・√13
△PRB:△BRQ=2:3だから、
BR=9/5・√13×2/3=6/5・√13cm
@別解@
実は△RBC≡△RCD
BC=DC(正方形一辺)、RC=RC(共通辺)
∠RCB=∠RCD=45°で二辺夾角が等しいから。
もしくは、ACは正方形の対角線で前問の△ABR≡△ADRから、
残りの△RBCと△RCDも対角線ACを対称の軸として左右対称となる→合同
BR=DR、DQまで求めてDR(②)をだせば良い。
△DQCの三平方は視野を広くみないと気づきにくい。
そこで、正方形内部でのRの位置に着目しても可。
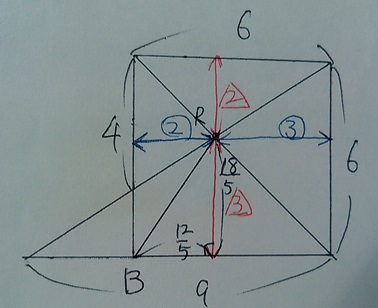
②(=12/5)と△3(=18/5)の三平方でBRが求まる。
大問5(回転移動)-31.1%
規則じゃなくなっている(´゚Д゚`)
突然の心変わりでビビるが、規則よりやり易いかもしれない。
(1) 42.0%
頂点Aの回転移動
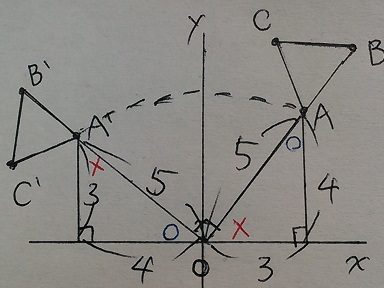
↑合同図形があります。
理由は、OA=OA’(半径)、○+×=90°で記号をふっていくと
直角三角形の合同条件である、斜辺と1つの鋭角が等しくなる。
3と4は逆になる。 A’(-4、3)
(2) 73.4%・6.8%!
OAは3:4:5、OA=5cm
問題はOC・・

正三角形を縦に分割。
Cを通るABに垂直な線分をひき、交点をDとする。
△CADは1:2:√3の直角三角形。
△CODで三平方 。
OC=√(√32+62)=√(3+36)=√39cm
OCを1辺とする直角三角形を、どこに見定めるか。
△CAD→△CODと視点を変えられるか。
次にも関わるので、合否の分水嶺となる重要な問題。
(3) 2.2%!!
見慣れた形である。移植
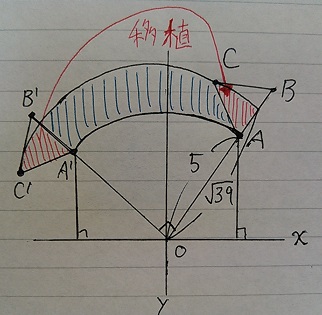
左の赤を右の赤へ移植すると・・
デカい4分の1円から小さい4分の1円をひく。
√39×√39×π×1/4-5×5×π×1/4
=(39-25)×π×1/4
=14/4π=7/2πcm2
解法はわかりやすいが、前問をミスるとドミノ式で本問も失点する。
2題で配点が8なので上位校受験者は落とせない。恐怖の落とし穴。



コメント