平均51.4点(前年比;-3.1点)

問題はこちら→リセマムさん
大問1(計算)-81.6%
(1) 98.4%
-2+9
=7
(2) 82.2%
-52+18÷3/2
=-25+12
=-13
(3) 77.5%
2(x+4y)-3(1/2x-1/3y)
=2x+8y-3/2x+y
=1/2x+9y
(4) 72.1%
x-7=(4x-9)/3 ←両辺3倍
3x-21=4x-9
x=-12
(5) 89.6%
√50+6√2-14/√2
=5√2+6√2-7√2
=4√2
(6) 69.9%
2x2-32
=2(x2-16)
=2(x+4)(x-4)
大問2(小問集合)-46.1%
(1) 57.7%
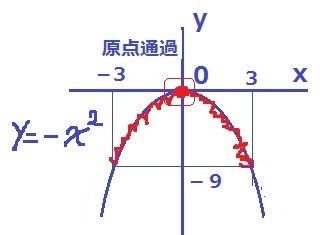
傾きが負なので、上に凸の放物線。
y=0→必ず原点を通過する。
また、y=-9なので、xは-3か3のいずれかに触れる。
エしかない。
(2) 74.9%
9÷36=0.25
(相対度数は分数ではなく小数で求めよう)
(3) 61.7%
△ABCで三平方→BC=√(62-52)=√11
5×√11÷2×6=15√11cm3
(4) 28.3%!
有理数…整数の分数で表せる数。
√ab/2を整数の分数で表すにはルートを外す。
すなわち、aとbの積が平方数であればいい。
ab=1…(1、1)
ab=4…(1、4)(2、2)(4、1)
ab=9…(3、3)
ab=16…(4、4)
ab=25…(5、5)
ab=36…(6、6)
計8通り→8/36=2/9
(5) 7.7%!!
昨年より難易度あげてきた:;(∩´_`∩);:
『120°の作図→反対側に60°をつくる』
60°の方が圧倒的に作りやすい。
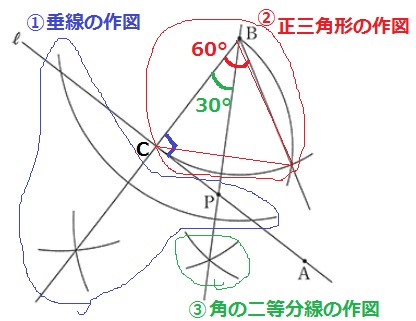
公式解答から拝借。3つの作業を要する。
①Bからℓに向けて垂線を作図。
(交点をCとすると、∠BCP=90°)
②BCを1辺とする正三角形(60°)の作図。
③角の二等分線で60°を半分にする。
△BCPは30°-60°-90°の直角三角形。
∠BPC=60°だから、反対側の∠APB=120°
大問3(関数)-41.0%
(1) 82.5%
A(3、4)をy=ax2に代入する。
4=9a
a=4/9
(2)① 36.7%
△OABは3:4:5の直角三角形→OA=5
B(-5、0)
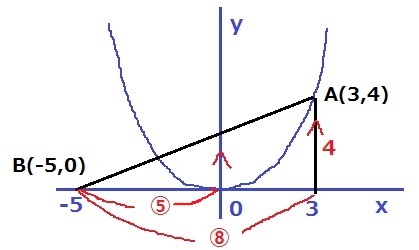
傾きは右に8、上に4だから、4/8=1/2
切片は相似を利用して、4×5/8=5/2
y=1/2x+5/2
② 3.9%!!
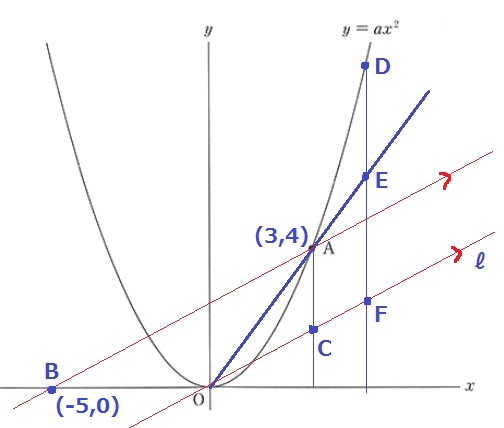
E・Fの位置に注意!

AC//EFから、△OAC∽△AEF
ありがたいことに面積比が平方数となっており、
△OACの面積を【16】とすると、△OEFの面積は【25】
辺の比は面積比の2乗だから、OC:OF=4:5
Aのx座標が3なので、Dのx座標は3×5/4=15/4
Dのy座標はy=4/9x2に代入。
y=4/9×(15/4)2=25/4
D(15/4、25/4)
大問4(平面図形)-44.5%
(1)
はじめは△OAC≡△OBCの証明。
a 97.6%
半径を指摘すればいい。OA=OB ウ
b 68.6%
直角三角形の合同条件、斜辺と他の1辺が等しい。カ
c 6点-11.0%! 3点-5.4% 無答-46.2%
うえの合同をもとに、△EAD∽△EFBを証明する。
辺の情報がないので角度攻め。
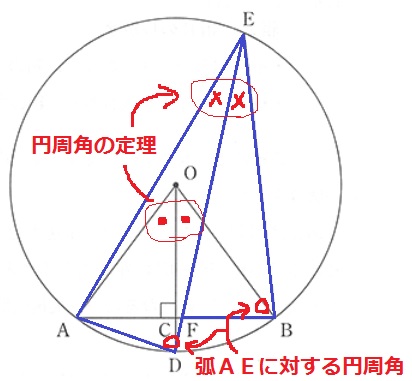
1つは弧AEに対する円周角。
もう1つは合同で示した2つの等角(●)をセットで円周角にして×にする。
どこかで経験していないと思いつきにくいかも…。
△OACと△OBCの各々の3つの角から使えそうな角を見極め、
その角と△EAD、△EFBの角との関係性を考え、円周角の定理を引き出したい。
(円に囲まれている図形は円周角の定理)
(2) 0.8%!!!
本試験の最難関。
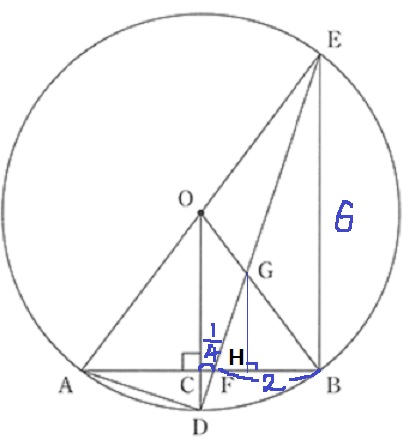
前問の∽から、AD:DE=FB:BE=1:3
BF=6×1/3=2cm
CF:FB=1:8より、CF=2×1/8=1/4cm
求めたいのは△GFBの面積。
底辺は2cmとわかったので、高さであるGHが知りたい。
GHを1辺とする三角形の相似を使うのだろうが、そこで避けて通れないのは半径の長さ。
直角の同位角よりOD//EB
ここから相似図形を見出せるので、半径のODがどうしても知りたい。
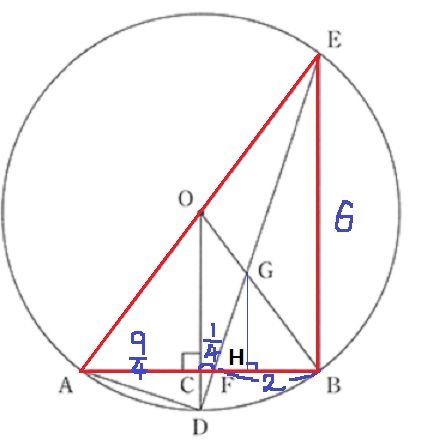
△OAC≡△OBCを用いる。
AC=BC=9/4より、AB=9/4×2=9/2cm
△ABEで三平方→直径AE=15/2cm
半径OD=15/2÷2=15/4cm
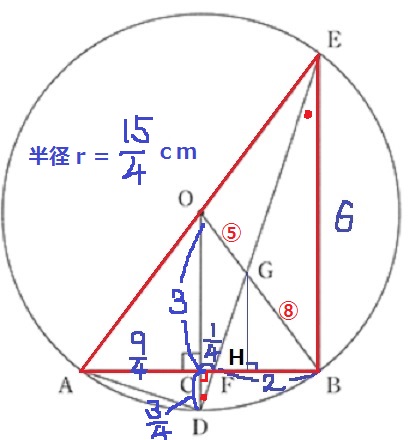
すると、いろんな場所が判明する。
△EBF∽△DCFから、CF:CD=BF:BE=1:3
CD=3/4cm
OC=15/4-3/4=3cm
△ODG∽△BEGより、
OG:BG=OD:BE=15/4:6=⑤:⑧
△OBC∽△GBHより、
GH=3×⑧/⑬=24/13cm
△GFBの面積は、2×24/13÷2=24/13cm2
@別解@
OC=3cmは、CがABの中点にあること利用し、
△AOC∽△AEBから、OC=6÷2=3cmと出せる。
CDはCFから出せるので、△ABEの三平方を経由せずとも解けた。
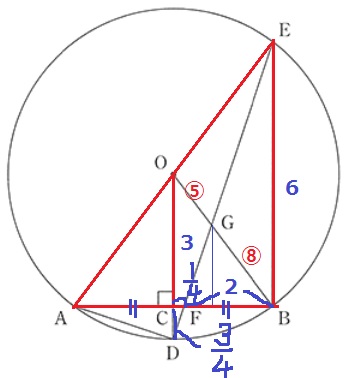
これが最も省エネかな?
@別解2@
Kさんから素晴らしい解法を頂きました。
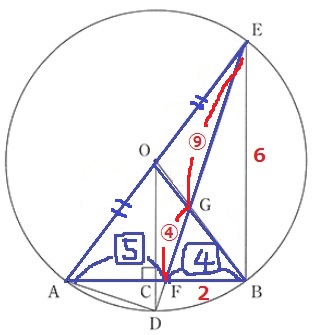
AC=BC=9/4から、AF:FB=5/2:2=5:4
青線でメネラウスの定理を適用。
EG/GF×4/9×1/1=1
EG:GF=9:4
△BEF→△BGF
2×6÷2×4/13=24/13cm2
*ODに触れず、△BGFの面積を直接求めにいく解法です。
Kさんは今年、千葉入試を受験した現役の中学生で、
サボが思いつかなかった素早い手法で解くとは恐れ入りました( ;゚д゚)
■続報■
Kさんは県立千葉高校へ進学しました。おめでとうございます。
大問5(総合問題)-37.5%
(1) 72.6%
2×3×3×5×5=450個
(2) 42.0%
素因数分解の要領で÷3、÷5をする。
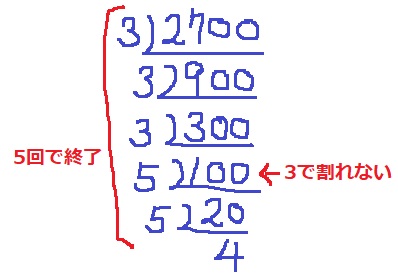
27が3の倍数なので、はじめは÷3を連続。
100から÷5をして、合計5回で終了。
4個が答え。
(3) 4点-12.4%! 2点-10.6% 無答-50.8%
公式解答の通り。
箱Xではビー玉がx倍に増えるので、
1×32×5×x2=540x
xについて解く。
45x2-540x=0 ←両辺を÷45
x2-12x=x(x-12)=0
xは自然数なので、x=12
(4) 17.5%!
4個から1000個を超えるようにするには、
倍率を1000÷4=250倍より大きくする。
◆4回すべてが×5
54=625倍・・・条件適合〇
4回すべてが裏は1通り。
◆4回中1回だけ×3
53×3=375倍・・・条件適合〇
4回中1回だけが表は4通り。
◆4回中2回だけ×2
52×32=225倍・・・条件不適合×
もうない。
コインの出方は24=16通りだから、確率は5/16。
@2020年度千葉(前期)解説@
社会…平均60.7点 理科…平均48.8点 英語…平均54.6点 国語…平均46.0点
@2020年度千葉(後期)解説@
数学…平均59.0点 社会…平均62.1点 理科…平均59.7点 英語…平均51.5点 国語…平均54.7点
その他は下記のリンクの目次からどうぞです。




コメント