平均18.7点(前年比;-3.1点)
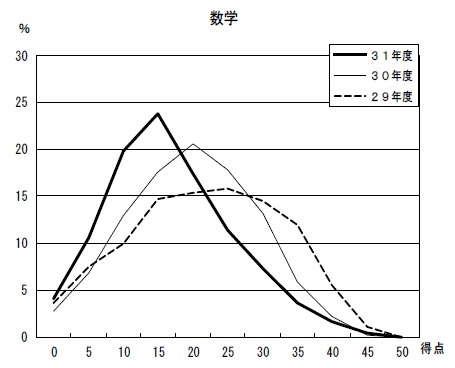
問題はこちら→リセマムさん
大問1(小問集合)
(1)
-9-6÷3
=-9-2
=-11
(2)
3a+2-(1/3a+1)
=3a+2-1/3a-1
=8/3a+1
(3)
90=2×32×5
(4)
(√8+1)(√2-3)
=(2√2+1)(√2-3)
=4-6√2+√2-3
=1-5√2
(5)
ネジレの位置…平行でなく、かつ延長しても交わらない。
直線CD
(6)
ア…n角形の内角の和⇒180(n-2)
イ…n角形の外角の和⇒360
n角形の内角の和+n角形の外角の和
=180(n-2)+360
=180(n-2)+180×2
=180(n-2+2)=180n
(7)
4つの玉を順番をつけて2つ取り出す→4×3=12通り
a2×b÷2ab2
=a/2b=1
a=2b、すなわち、aがbの2倍になる組み合わせを考える。
(a、b)=(2、1)(4、2)
確率は、2/12=1/6
(8)
1年生は7人。この中央値は4番目の15m
2年生は8人。この中央値は4~5番目の平均値。
xを除いて数えていくと、4番目は14m、その次が17m
ということは、xが16mであれば、中央値が15mになる。
x=16
(9)
x=2、y=3を代入。
2a+3b=1…①
2b-6a=8…②
これを解いて、a=-1、b=1
大問2(平面図形・文字式)
(1)①
Aは正方形、BとCは長方形。
ア~ウはすべて当てはまる。
エ(対角線の直交)だけはAのみ。
②
∠QPRの前に、∠QORを経由した方がわかりやすいかと。
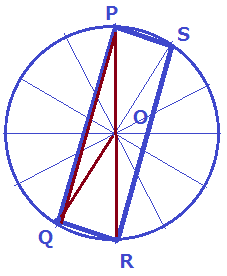
∠QORは1周を12分割するから、360÷12=30°
円周角の定理から、∠QPR=30÷2=15°
③
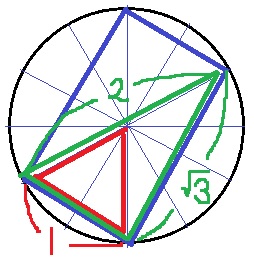
角度を調査すると、赤い三角形は60°ずつで正三角形。
長方形の横の長さは、半径と同じ1cm。
長方形を対角線で区切ると、30°-60°-90°の直角三角形が見つかる。
1:2:√3から、長方形の縦の長さは√3cm
1×√3=√3cm2
(2)①
りんごの可食部は、100-15=85%
200×85%=170g
②
150gのバナナがx本。
可食部は60%。それに含まれるエネルギーは80/100
y=150x×60%×80/100=72x
ウ
③
前問の答えを利用する。
y=72xで、y=1224を代入。
72x=1224
x=17 →17本
大問3(方程式)
(1)
ア:12500+(450+100)×10=18000
イ:y=7500+(550+150)x→700x+7500
ウ:A社-y=700x+7500、B社-y=550x+12500
700x+7500=550x+12500
x=100/3
(2)①
基本料金…7500円
Tシャツ代…550×40=22000円
プリント代…150×(40-20)=3000円
以上を合計すると32500円
②
20枚より多いときを考えると、A社の代金はTシャツ代の550円が増えていく。
グラフの傾きは550となり、B社の傾きと等しくなる。
傾きが等しい=平行
20枚の時点でAはBよりも値段が安いので、20枚以降の傾きが平行であれば、
A社の方がB社より必ず安くなる。
(公式解答)グラフの傾きはともに550で、2つの直線は平行
大問4(数量変化)
(1)①
3秒後は、AP=3cm、AQ=3cmの直角二等辺三角形。
△APQ:3×3÷2=9/2cm2
②
0≦x≦4は、底辺と高さがともに増えていくので、面積は倍々に増えていく。
図2で(4、8)の座標を通るので、これをy=ax2に代入。
8=16a
a=1/2
y=1/2x2
③
8秒後にPはA、QはCに到着し、△APQの面積yは0になる。
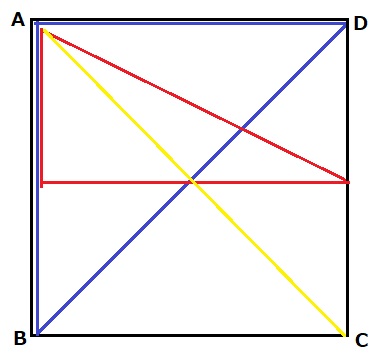
4≦x≦8では、青→赤→黄と変化していく。
APの長さが短くなり、AD方向の長さが変わらない。
→△APQの面積は、グラフ上では直線で減っていく。
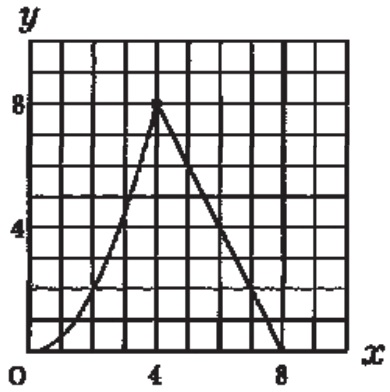
(4、8)と(8、0)を結ぶ。
④
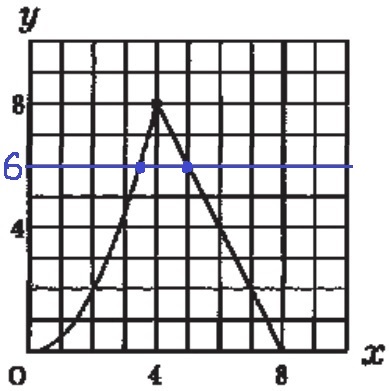
y=6のときのx座標2つが答えとなる。
4≦x≦8のときは傾きが-2(右1下2)で、x=5
0≦x≦4のときは、②よりy=1/2x2だから、
6=1/2x2
x>0よる、x=2√3
x=2√3、5
(2)
区切りの良いところで調査する。
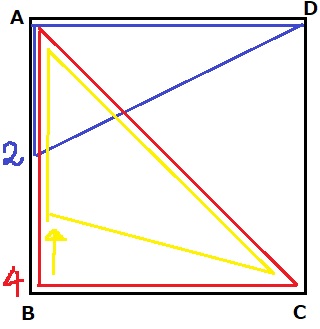
青→赤→黄
青は2秒後。QがDにくる。
0≦x≦2では、APとAQがともに増えるので、yは放物線で増えていく。
赤は4秒後。PがB、QがCにくる。
2≦x≦4では、AB方向は増えていくが、AD方向は変わらない→直線で増える。
4秒以降が黄色。PがAに戻っていき、QはCで止まっている。
4≦x≦8では、面積が直線的に減っていき、PがAにつくと0になる。
ア
(3)
△APQの面積が8cm2となるとき⇒AB方向で4cm、AD方向で4cm。
AB方向の4cmはAP=4、すなわち、PはBにいなければならない。
PがB以外にいるとAP<4になり、AD方向もMaxで4だから、△APQは8未満になる。
『2点P、QがAを出発してから4秒後』となり、『点Pの位置は点B上にある』
Qは一度Dに到達してしまえば、AD方向の長さが4cmのまま。
つまり、『点Qの位置は辺CD上にある』
*ちなみに、点Qの速さが毎秒1cm未満だと、QがDに着く前にPがBに着いてしまう。
Qは辺CD上にくれば△APQの面積が8cm2になる可能性はあるが、
PはBに来た瞬間にしか△APQが8cm2にならない。
だから、PがBにくる前にQがDを通過しておく必要があるので、
Qの速さはP以上でなくてはならない。
大問5(平面図形)
(1)
角の二等分線の作図。
①Bを中心に適当な弧を描く。
②AB、ACとの交点を中心に適当な弧を描く。
③上の交点とBを結ぶ。
(2)①

△ABCが二等辺三角形ゆえ、
∠ABC=∠ACB=(180-36)÷2=72°
∠ABD=72÷2=36°
△ABDで外角定理→∠BDC=36+36=72°
②

△BCDと△ABDの底角が等しく、二等辺となる。
線分ADと線分BD
③

BC=xとすると、AD=x、CD=1-x
△ABC∽△BDC(2角)
AC:CB=BC:CD
1:x=x:(1-x)
x2=1-x
x2+x-1=0
解の公式を適用。
x=(-1±√5)/2
x>0より、x=(√5-1)/2
@余談@
本問の二等辺三角形は、初等幾何の世界ではよく知られている形である。
問題ではACを1とおいたが、BCを1とおくと、
BC:AC=1:(1+√5)/2となり、
これは幾何的に美しい比率といわれる黄金比で自然界にもみられる。
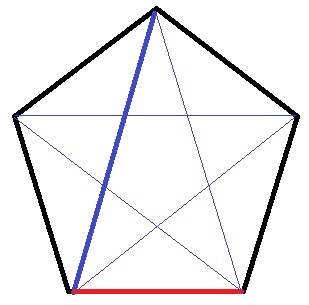
正五角形の1辺(赤)を1とすると、対角線(青)は(1+√5)/2で黄金比。
問題の相似図形はここからきている。
(2)①
2つの円が接しているとき、中心から接点に向けて半径を伸ばすと、
2つの半径(QSとSR)は一直線になる。
〔線分QRと円O2の交点〕を点Sとする。
②
半径から長さを認定していく。
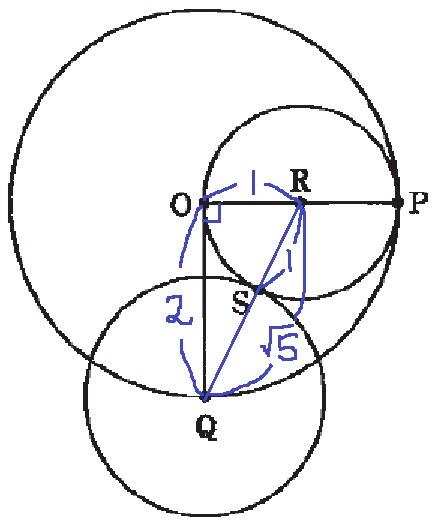
△OQRで三平方→QR=√5
O3の半径(QS)=√5-1cm
③
△OQTと△ABCの相似を証明する。
別の問題で登場した図形と比較するのでビックリする:;(∩´_`∩);:
誘導では、OQ:AB=OT:AC=2:1が導かれている。
2辺の比が等しい点が指摘されたので、3辺の比か2辺の比と間の角。
しかし、図4では∠QOTがわからない…。
そこで、残る辺の辺であるBCとQTの長さを調べる。
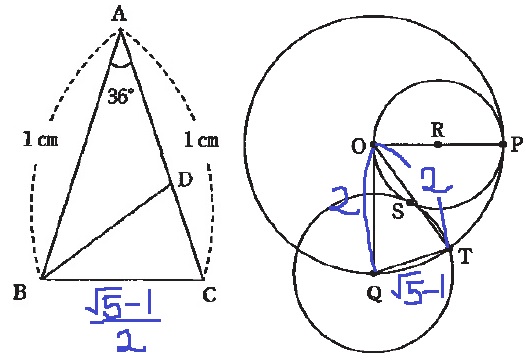
(1)③より、BC=(√5-1)/2
(2)②より、O3の半径からQT=√5-1
QT:BC=2:1
3辺の比が2:1で等しい→∽
@余談@
本問の図形から正五角形を作図することができる。

QRを延長。円O2との交点をVとする。
QVの長さをとり、右側へ移行。円O1との交点がW。
W・Tの反対側も同様にとり、Uを含めすべて結ぶと正五角形になります。




コメント
つこまて
けさみふ
ひきてな