問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
－６2＋４÷（－２/３）
＝－36－６
＝－42
（２）
４ａｂ2÷６ａ2ｂ×３ａｂ
＝２ｂ2
（３）
√48－３√２×√24
＝√48－３√48
＝－２√48
＝－８√３
（４）
４ｘ＋３ｙ＝－７ …①
３ｘ＋４ｙ＝－14 …②
係数が…(;`ω´)
①＋②をすると、７ｘ＋７ｙ＝－21
ｘ＋ｙ＝－３ …③
①－②で、ｘ－ｙ＝７ …④
③と④を解くと、ｘ＝２、ｙ＝－５
（５）
ｘｙ＝（√５＋３）（√５－３）＝（√５）2－３2＝－４
ｙ－ｘ＝（√５－３）－（√５＋３）＝－６
ｘｙ2－ｘ2ｙ
＝ｘｙ（ｙ－ｘ）
＝－４×（－６）
＝24
（６）
ｙ＝16/ｘ
→ｘｙ＝16
16の約数は５個。
反比例は双曲線、ｘは負の数を含むから10個。
*原点Ｏは通らない。
（７）
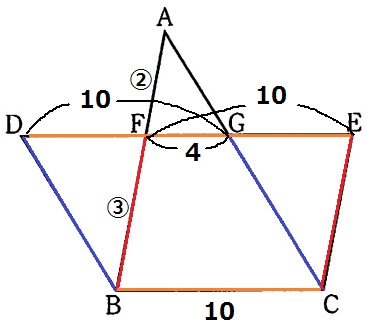
同色の部分が平行。
四角形ＤＢＣＧと四角形ＦＢＣＥは２組の対辺が平行だから平行四辺形。
ＢＣ＝ＤＧ＝ＦＥ＝10ｃｍ
△ＡＦＧ∽△ＡＢＣの辺の比は②：⑤なので、ＦＧ＝10×②/⑤＝４ｃｍ
ＤＥ＝10＋10－４＝16ｃｍ
＠別解＠
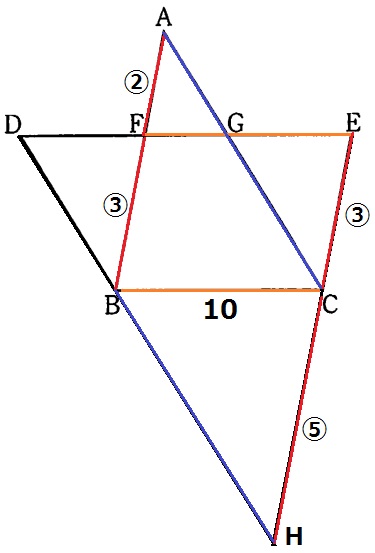
ＤＢとＥＣを延長した交点をＨとする。
平行四辺形ＦＢＣＥの対辺で、ＥＣ＝③
平行四辺形ＡＢＨＣの対辺で、ＣＨ＝⑤
△ＢＨＣ∽△ＤＨＥより、ＤＥ＝10×⑧/⑤＝16ｃｍ
（８）
３年生の箱ひげ図を描く。
データを昇順にすると、【24、28、28、31、33、35、39、40】
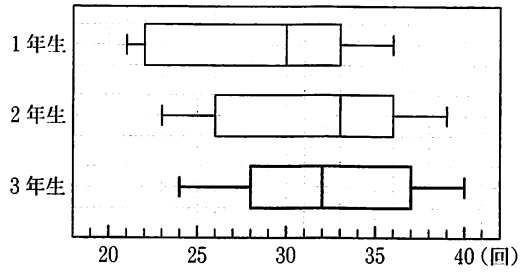
最小値は24回、最大値は31回。
８人の中央値（第２四分位数）は４番目と５番目の平均で32回。
第１四分位数は下位４つのうち、下から２番目と３番目の平均で28回。
第３四分位数は上位４つのうち、上から２番目と３番目の平均で37回。
大問２（空間図形）
（１）
円柱＋円錐
＝５×５×π×３＋４×４×π×３÷３
＝91πｃｍ3
（２）
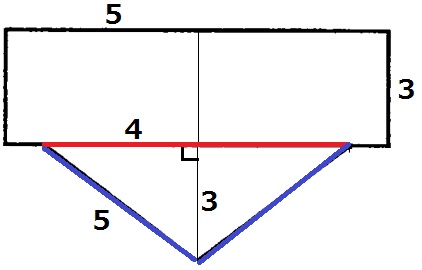
円錐を抜かした円柱だけの表面積は、
５×５×π×２＋５×２×π×３＝80πｃｍ2
円錐をくっつけると赤い部分（半径４ｃｍの円）が減り、青い部分（円錐の側面積）が増加する。
円錐の母線は３：４：５の直角三角形から５ｃｍ。
円錐の側面積は【母線×半径×π】で計算する。
80π－４×４×π＋５×４×π＝84πｃｍ2
大問３（確率）
（１）
全体の取り出し方は、３×３＝９通り
Ｘ＞Ｙとなる組み合わせを調べる。
Ｘ＝９のときは２通り、Ｘ＝12のときは３通りで合計５通り。
確率は５/９。
（２）
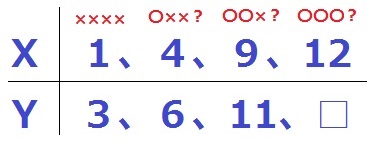
Ｙの１枚がわからない状態でＸ＞Ｙとなる組み合わせは、
（Ｘ、Ｙ）＝（４、３）（９、３～６）（12、３～11）の６通り。
２枚の取り出し方は４×４＝16通りだから、
Ｘ＞Ｙとなる組み合わせが、16÷２＝８通りあればいい。
あと２通り必要だから、Ｘ＝９、12の？は〇でなければならない。
（Ｘ＝４の？は×）
Ｙの残りの１枚は４～９のあいだであるイ・ウ・エ。
大問４（数量変化）
（１）
ｘ＝１のとき、ＰとＱは毎秒１ｃｍだから、ＡＰ＝ＤＱ＝１ｃｍ
ｙ＝１×１÷２＝１/２
０≦ｘ≦６では、△ＡＱＰの底辺ＡＰ、高さＤＱがともに伸びるので、
△ＡＱＰの面積はｙ＝ａｘ2で増加する。
６≦ｘ≦12では面積が変わらない。12≦ｘ≦18では高さＤＱの減少で面積は一次関数で減少。
ｘ＝18でｙ＝０となる。
ｙ＝１/２、ウ
（２）
△ＲＱＤの面積の変化を追う。
０≦ｘ≦６、底辺ＤＱが増加するので面積は比例で増加。ｘ＝６のとき、ｙ＝６×３÷２＝９
６≦ｘ≦12、底辺ＲＤは一定で高さが減少。面積は一次関数で減少。ｘ＝12のとき、ｙ＝０
12≦ｘ≦18、高さが増加⇒面積は一次関数で増加。ｘ＝18のとき、ｙ＝９
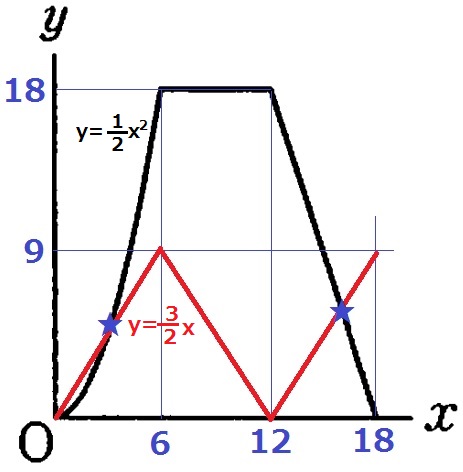
グラフに載せる。
（交点★のｘ座標が答えだが、ｙ座標の高さがズレてしまった・・）
前問で放物線はｘ＝１のときｙ＝１/２だった→ｙ＝１/２ｘ2
（６、９）を通る比例→ｙ＝３/２ｘ
１/２ｘ2＝３/２ｘ
ｘ2＝３ｘ
ｘ2－３ｘ
＝ｘ（ｘ－３）＝０
０＜ｘ≦18だから、ｘ＝３
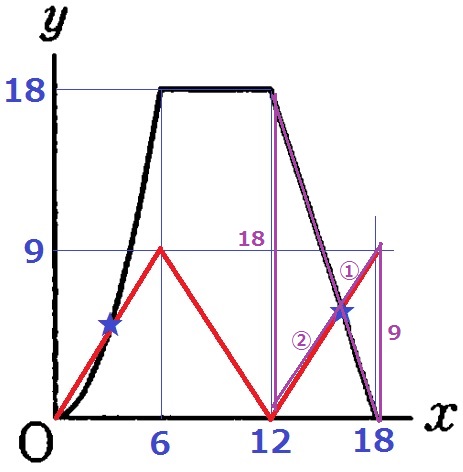
後半は紫の三角形で相似を用いる。
相似比は２：１で、ｘ座標の差の６が③にあたるから、
交点のｘ座標は、12＋６×②/③＝16
ｘ＝３、16
大問５（平面図形）
（１）
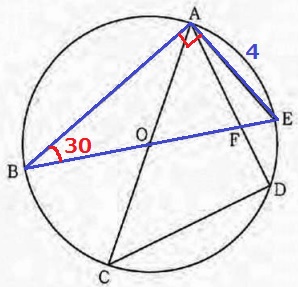
直径ＢＥに対する円周角から、∠ＢＡＥ＝90°
△ＡＢＥは１：２：√３の直角三角形→直径ＢＥ＝８ｃｍ
（２）
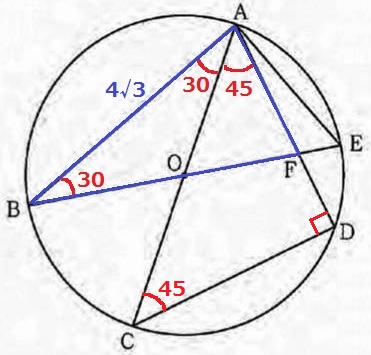
直径ＡＣに対する円周角より、∠ＡＤＣ＝90°
△ＡＣＤは直角二等辺三角形で、∠ＣＡＤ＝45°
半径ＯＡ＝ＯＢから△ＡＢＯは二等辺→∠ＢＡＯ＝30°
△ＢＦＡに着目すると、残りの角である∠ＢＦＡ＝180－（30＋30＋45）＝75°
∠ＢＡＦ＝∠ＢＦＡより、△ＢＦＡは底角が等しいから二等辺三角形。
ＢＡ＝ＢＦ＝４√３ｃｍ
ＥＦ＝ＢＥ－ＢＦ＝８－４√３ｃｍ
（３）
△ＯＢＧは半径ＢＯ＝４ｃｍ、∠ＢＯＧ＝30＋30＝60°
弧ＡＤの円周角から、∠ＡＢＤ＝∠ＡＣＤ＝45°なので、
∠ＯＢＧ＝45－30＝15°…
直接、面積を出そうとしても求めづらい(*_*)
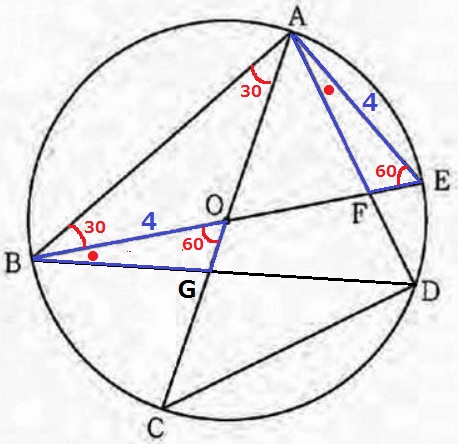
ＡＥ＝４ｃｍから△ＥＡＦと△ＯＢＧの関係性に着目すると、
ＡＥ＝ＢＯ＝４ｃｍ、弧ＤＥの円周角より∠ＥＡＦ＝∠ＯＢＧ、
∠ＡＥＦ＝∠ＢＯＧ＝60°から、１辺両端角相等で△ＥＡＦ≡△ＯＢＧ
△ＥＡＦの面積を求めればいい。
前問でＥＦを出しているので、高さがわかればいい。
対頂角で∠ＡＯＥ＝60°
残りの角も60°なので、△ＥＡＯは１辺４ｃｍの正三角形。
三平方より高さは２√３ｃｍ。
△ＥＡＦ（△ＯＢＧ）の面積は、（８－４√３）×２√３÷２＝８√３－12ｃｍ2
大問６（規則）
（１）
タイルＡは平方数で増えていく。
５番目は、５×５＝25枚
（２）
タイルＢは格子状に並ぶので、格子で捉える。
１番目は１枚の縦横が２本ずつ、１×（２×２）＝４枚
２番目は２枚の縦横が３本ずつ、２×（３×２）＝12枚
３番目は３枚の縦横が４本ずつ、３×（４×２）＝24枚
12番目は12本の縦横が13本ずつ、12×（13×２）＝312枚
（３）
ｎ番目のタイルＡはｎ2枚。
タイルＢはｎ×（ｎ＋１）×２＝２ｎ2＋２ｎ枚
（２ｎ2＋２ｎ）－ｎ2
＝ｎ2＋２ｎ＝360
ｎ2＋２ｎ－360
（－360だから＋と－の組み合わせ。和が２と少ない。
360の約数のうち、積が360となり差が最も少ない２数を探す）
＝（ｎ＋20）（ｎ－18）＝０
ｎ＞０だから、ｎ＝18
大問１
（３）48はあとで処理すると良いかも。
（４）係数の差が１で、ｘとｙの和差が出せる。
もちろん、最小公倍数12で統一しても良い。
（６）負の数を含む、積が16となる組み合わせ。
（７）難しくはないが、個人的に好きな問題でした。
大問２
（２）最初は円柱だけを考え、下に円錐をつけたときの表面積の増減を調べる。
大問３
（２）４枚ずつだから全体は16通り→８通りずつに分ければ勝率が同じ。
残り１枚が不明の状態でＸ＞Ｙとなる場合を数える。
２個不足→９と12は勝たせる→４と９のあいだ。
大問４
（２）△ＲＱＤの変化を調べなければならず、時間がとられる。
大問５
（２）有名三角形が２種類でてくるので、角度を調査する。
△ＡＢＦは頂角30°の二等辺三角形。（１）の直径が使える。
（３）ここも前問の利用に思いを寄せたい。
大問６
等差数列の和の出題ではなかった。
（２）縦横で考えるのが良い。
（３）前問ができれば取りやすい。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント