2018年度　神奈川県公立高校入試・追検査【数学】解説

問題はコチラから→ＰＤＦファイル
採点上の注意によると、問７（ア）以外に中間点がない。

大問１（計算）

（ア）
－13＋２＝－11　【２】

（イ）
３/８－３/５＝－９/40　【２】

（ウ）
30ａ²ｂ²÷（－６ａｂ）＝－５ａｂ　【１】

（エ）
－25/√５＋√20
＝－５√５＋２√５＝ｰ３√５　【４】

（オ）
－（ｘ－２）²＋（ｘ－８）（ｘ＋３）
＝－ｘ²＋４ｘ－４＋ｘ²－５ｘ－24
＝－ｘ－28　【３】

大問２（小問集合）

（ア）
（ｘ－３）²＋５（ｘ－３）－36　←（ｘ－３）をＸに置き換えると…
＝Ｘ²＋５Ｘ－36
＝（Ｘ＋９）（Ｘ－４）　←Ｘを（ｘ－３）に戻す
＝（ｘ－３＋９）（ｘ－３－４）
＝（ｘ＋６）（ｘ－７）　【３】

（イ）
５ｘ²－８ｘ＋１＝０
因数分解はできないので解の公式。
ｘの係数が偶数なので、ｂ＝２ｂ’verが使える。
ｘ＝４±√11/５　【１】

（ウ）
ｙ＝ａｘ²において、
ｘ＝－４のとき、ｙ＝16ａ
ｘ＝－１のとき、ｙ＝ａ
変化の割合＝（ｙの増加量/ｘの増加量）
（16ａ－ａ）/{－４－（－１）}＝－５ａ
一方、比例であるｙ＝－３ｘの変化の割合は傾きの－３だから、
－５ａ＝－３
ａ＝３/５　【４】

＠別解＠
ｙ＝ａｘ²において、ｘの値がｐ→ｑのときの変化の割合はａ（ｐ＋ｑ）。
（－４－１）ａ＝－３
ａ＝３/５

（エ）
中学受験のやり方です。

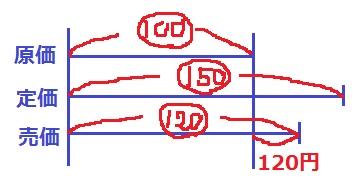
原価を【100】とおくと、50％増しの定価は【150】となる。
売価は、【150】×８/10＝【120】
原価との差である【20】が120円に相当する。
原価は、120×100/20＝600円　【４】

（オ）
50Ｌから５ａの水を抜き、それが20Ｌ以上。
50－５ａ≧20　【１】

（カ）
苦手な人が多そう。。

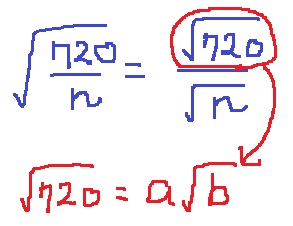
√（720/ｎ）を√720/√ｎに変換。
分子の√720をａ√ｂの形に変えたとき、
ｎの値がｂであれば、√ｂと√ｎが約分して全体が整数値になる。
言い換えれば、√720をａ√ｂに変換できる場合の数を求める。

720＝２⁴×３²×５
ａは根号計算で平方数になるので、２×２、３×３、２×２×２×２、
２×２×３×３、２×２×２×２×３×３のどれか。
√720＝２√180＝３√80＝４√45＝６√20＝12√５
ｎ＝720、180、80、45、20、５の６個。【２】
*ａ＝１であれば、ｎ＝720も整数になることに注意！

大問３（小問集合２）

（ア）
求めにくい:(っ`ω´c):

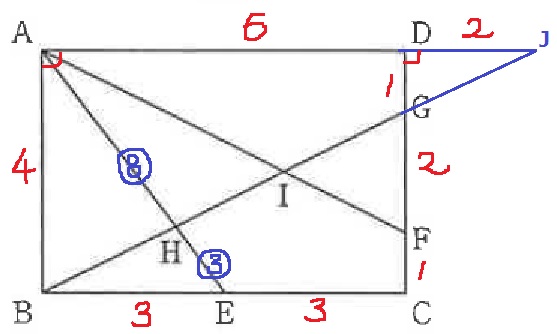
オーソドックスな手法で延長してみる。
ＢＧとＡＤの交点をＪとする。
△ＢＣＧ∽△ＪＤＧより、ＤＪ＝６×１/３＝２ｃｍ
また、△ＡＨＪ∽△ＥＨＢより、ＡＨ：ＥＨ＝ＡＪ：ＥＢ＝⑧：③

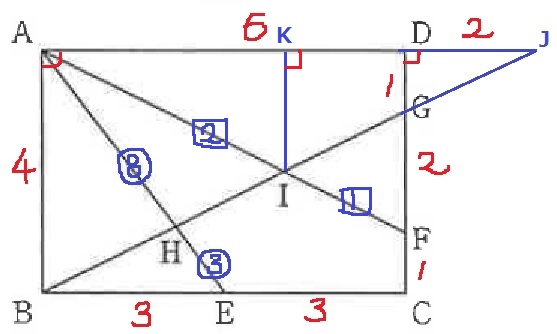
つづいて、△ＡＢＩ∽△ＦＧＩ
ＡＩ：ＦＩ＝ＡＢ：ＦＧ＝４：２＝２：１
△ＡＫＩ∽△ＡＤＦより、ＫＩ＝３×２/３＝２ｃｍ

あとは、△ＡＢＪ－△ＡＩＪ－△ＡＢＨをすれば△ＡＨＩがでる。
△ＡＢＨは、△ＡＢＥの面積から×⑧/⑪倍すればいい。
８×４÷２－８×２÷２－４×３÷２×８/11
＝８－48/11＝40/11ｃｍ²

ちなみに、連比で泥臭くやると、
ＢＨ：ＨＩ：ＩＧ：ＧＪ＝12：10：11：11になる。

（イ）
Ｇが２枚あるので、Ｇ₁、Ｇ₂と区別してみよう。
Ａ～Ｇ₂の８枚から２枚選ぶ組み合わせは、₈Ｃ₂＝28通り

隣り合うパターンは過不足なく調べる必要がある。
（ＡＢ）（ＡＦ）（ＡＧ）（ＢＣ）（ＣＤ）（ＣＧ）（ＤＥ）（ＥＦ）（ＥＧ）。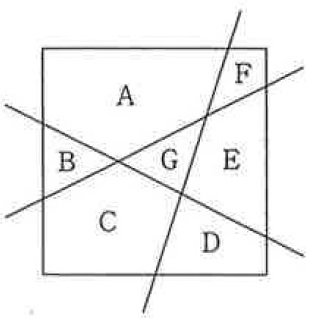
このうち、Ｇを含む組み合わせは、Ｇ₁とＧ₂で２つずつある！
全部で12通り。
12/28＝３/７

大問４（関数）

（ア）
ｙ＝３ｘ＋６の切片Ａの座標は（０、６）
Ｂ座標は（３、６）となり、これをｙ＝ａｘ²に放り込む。
６＝３²ａ
ａ＝２/３　【４】

（イ）ⅰ
Ｃはｙ＝３ｘ＋６とｘ軸との交点。
０＝３ｘ＋６
ｘ＝－２　→Ｃ（－２、０）

ＣＯ：ＯＥ＝４：９から、Ｅ（９/２、０）
また、ｙ＝３ｘ＋６より、Ｄ（－３、－３）

Ｄ（－３、－３）とＥ（９/２、０）を通過する直線の式を求める。
Ｄ→Ｅは、右に３＋９/２＝15/２、上に３なので、
傾きｍ＝３÷15/２＝２/５　【３】

ⅱ
Ｅ（９/２、０）を、ｙ＝２/５ｘ＋ｎに代入。
０＝２/５×９/２＋ｎ
ｎ＝－９/５　【５】

（ウ）
出だしを誤ると迷子になる。等積変形を用いる。

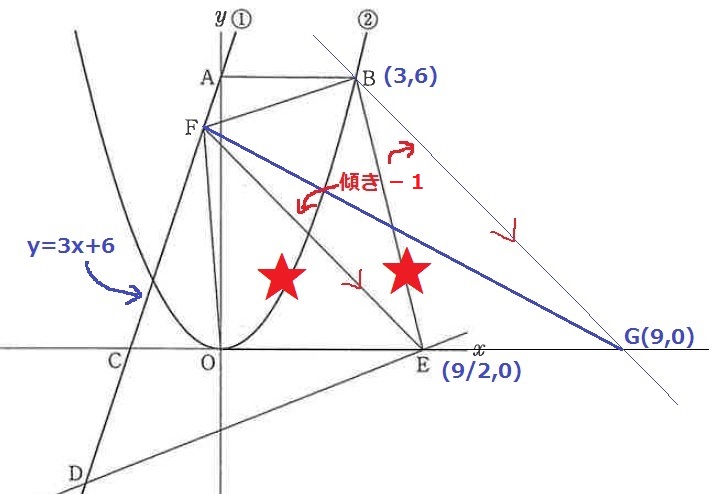
Ｂを通る、ＦＥに平行な線をひき、ｘ軸との交点をＧとする。
等積変形により、△ＦＥＢ＝△ＦＥＧ
△ＦＯＥ＝△ＦＥＧでこれらは高さが等しいので、底辺がＯＥ＝ＥＧとなる。
→Ｇのｘ座標は、９/２×２＝９

Ｂ（３、６）→Ｇ（９、０）
右に６、下に６で、ＢＧの傾きは－１。
同様に、ＦＥの傾きも－１。

Ｅ座標からＦＥの式を求める。
０＝９/２×（－１）＋ｂ
ｂ＝９/２
ＦＥ；ｙ＝－ｘ＋９/２

ＦはＦＥとＡＣの交点なので、
－ｘ＋９/２＝３ｘ＋６
ｘ＝－３/８

大問５（規則）

（ア）
全体の枚数と黒の枚数が求めやすいので、そちらを先に決めておく。

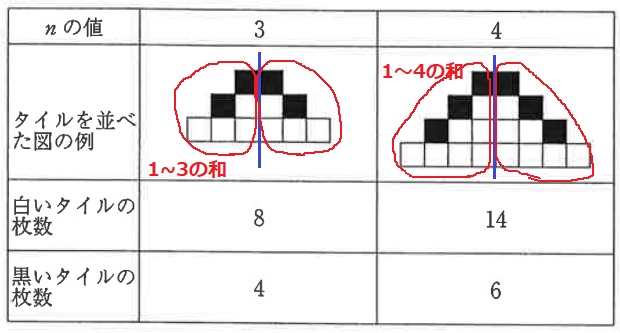
全体の枚数は、うえのように左右対称に分ける。
ｎ＝３であれば、１～３の和である６枚が左右合わせて12枚。
黒の枚数は、（３－１）×２＝４枚。
白は、12－４＝８枚となる。

ｎ＝６であれば、全体が（１～６の和）×２＝42枚
黒は、（６－１）×２＝10枚
白は、42－10＝32枚
よって、白と黒の差は32－10＝22枚　【２】

（イ）
全体は、１～ｎの総和×２枚。
１/２ｎ（ｎ＋１）×２＝ｎ²＋ｎ枚
黒は、（ｎ－１）×２＝２ｎ－２枚
白は、ｎ²＋ｎ－（２ｎ－２）＝ｎ²－ｎ＋２枚
白と黒の差が464枚なので、
ｎ²－ｎ＋２－（２ｎ－２）
＝ｎ²－３ｎ＋４＝464

ｎ²－３ｎ－460
＝（ｎ＋20）（ｎ－23）＝０
ｎ＞０より、ｎ＝23

＠別解＠
解法としては上のやり方で申し分ないのですが、
他の切り口がないか調べてみました。

左右で白黒の差が464枚なので、片方で白黒の差が232枚になればいい。
白黒の差（片方のみ）に注目すると、
ｎ＝３　２枚
ｎ＝４　４枚
ｎ＝５　７枚…

差に注目すると、＋２、＋３、＋４と増えている。
わかりやすいように、ｎ＝２を前につけて考えてみよう。
ｎ＝２のとき→１枚

白黒の差：【１、２、４、７、11、16、22、29、37……232】
差の差は＋１、＋２、＋３…。
１と232の差は231で、232とその手前の数との差をＫとすると、
１～Ｋ番目までの総和が231にあたる。
１/２Ｋ（Ｋ＋１）＝231
Ｋ²＋Ｋ－462
＝（Ｋ＋22）（Ｋ－21）＝０
Ｋ＞０より、Ｋ＝21

Ｋは232とその手前との数字の差。
＋１、＋２、＋３…＋20、＋21（＝Ｋ）
Ｋは１～232までのあいだの数の個数なので、232は白黒の差の数列の22番目。
最初の１はｎ＝２だったので、22番目にあたる232はｎ＝23。
素直に文字式で攻略した方がやりやすいね(;`ω´)

大問６（空間図形）

（ア）
立体図が与えられていない・・。
底面積はすぐわかるので、正四角錘の高さが知りたいところ。

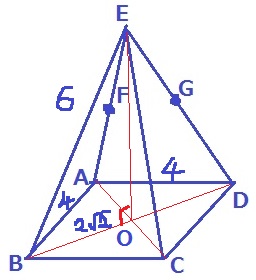
底面の正方形の対角線の交点をＯとする。
ＥＯが正四角錘の高さにあたる。
△ＡＢＤで三平方→ＢＤ＝４√２ｃｍ
ＢＯ＝４√２÷２＝２√２ｃｍ
△ＥＢＯで三平方→ＥＯ＝２√７ｃｍ
正四角錘の体積は、４×４×２√７÷３＝32√７/３ｃｍ³　【１】

（イ）
ＢＧを斜辺とする直角三角形に狙いをしぼる。

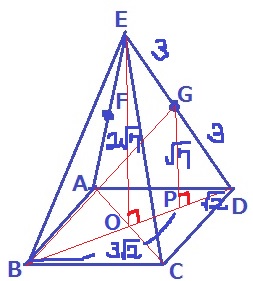
Ｇから垂線をひくとＢＤと交わり、そこをＰとする。
△ＥＯＤ∽△ＧＰＤから、辺の比はＥＤ：ＧＤ＝２：１
ＧＰ＝２√７÷２＝√７ｃｍ
ＰＤ＝２√２÷２＝√２ｃｍ
ＢＰ＝４√２－√２＝３√２ｃｍ
最後に、△ＧＢＰで三平方→ＢＧ＝５ｃｍ　【２】

（ウ）
面ＦＢＣＧで作図。

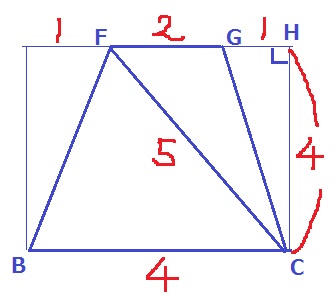
四角形ＦＢＣＧは等脚台形になる。
左右対称ゆえ、ＧＨ＝１ｃｍ
ＣＦの長さは、前問で求めたＢＧと同じで５ｃｍ。
△ＣＦＨで三平方→３：４：５より、ＣＨ＝４ｃｍ
△ＣＦＧの面積は、２×４÷２＝４ｃｍ²

大問７（平面図形）

（ア）
△ＢＦＧ∽△ＤＣＥの証明。

１つは、対頂角＋円周角（赤）。
もう１つは、∠ＡＣＥ＝∠ＥＣＤ＝●として、円周角で∠ＡＢＤ＝●●、
△ＢＤＦは二等辺。この外角が●●だから、∠ＢＦＧ＝●となる（黒）。
空欄は外角定理の説明と、それを使って⑧（∠ＢＦＤ＝１/２∠ＡＢＤ）に続く内容を書く。

以下、公式解答より。
（ⅰ）三角形の外角は、それととなり合わない２つの内角の和に等しい
（ⅱ）∠ＡＢＤ＝∠ＢＤＦ＋∠ＢＦＤ

（イ）

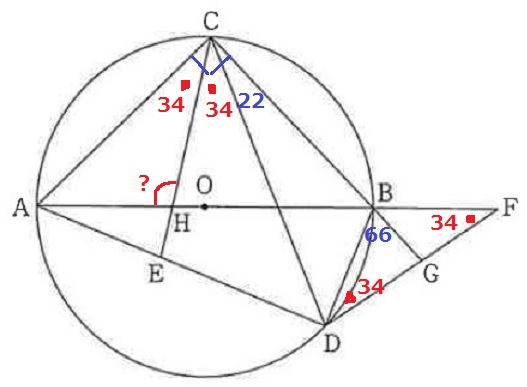
∠ＡＣＢは半円の弧に対する円周角で90°
●＝（90－22）÷２＝34°

△ＢＤＦの内角より、∠ＧＢＦ＝180－34×２－66＝46°
対頂角で、∠ＣＢＨ＝46°
△ＣＢＨで外角定理→∠ＡＨＣ＝34＋22＋46＝102°

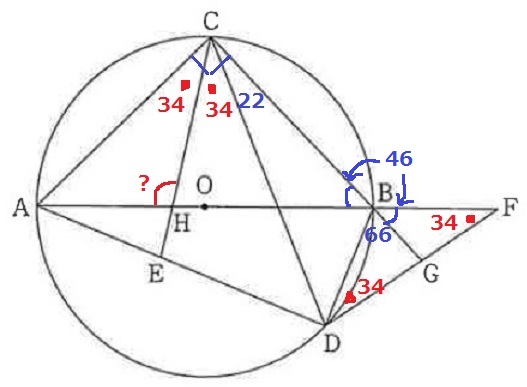
＠別解＠

△ＢＤＧで外角定理→∠ＢＧＦ＝66＋34＝100°
前問の相似より、∠ＣＥＤ＝100°

∠ＡＥＨ＝180－100＝80°
弧ＤＢに対する円周角より、∠ＥＡＨ＝∠ＤＣＢ＝22°
△ＡＥＨで外角定理→∠ＡＨＣ＝22＋88＝102°
公立高校入試解説ページに戻る