2023年度　大阪府公立高校入試Ｃ問題過去問【数学】解説

平均51.2点（前年比；－14.9点）
問題はコチラ→ＰＤＦファイル
2023年度・大阪（数学）Ａ問題、Ｂ問題の解説はコチラ。

大問１（小問集合）

（１）　100.0％
－ａ×（２ａｂ）²÷（－２/３ａｂ²）
＝－ａ×４ａ²ｂ²×－３/（２ａｂ²）
＝６ａ²

（２）　92.2％
（６＋√８）/√２＝６/√２＋√８/√２＝３√２＋２　
（６＋√８）/√２＋（２－√２）²
＝（３√２＋２）＋（６－４√２）
＝８－√２

（３）　96.4％
ａｘ²＋４ｘ－７ａ－16＝０にｘ＝３を代入。
９ａ＋12－７ａ－16＝０
ａ＝２

元の式にａ＝２を代入すると、
２ｘ²＋４ｘ－14－16
＝２ｘ²＋４ｘ－30＝０　←÷２
ｘ²＋２ｘ－15
＝（ｘ－３）（ｘ＋５）＝０
もう１つの解は、ｘ＝－５
ａの値…２、もう１つの解…ｘ＝－５

（４）　40.0％

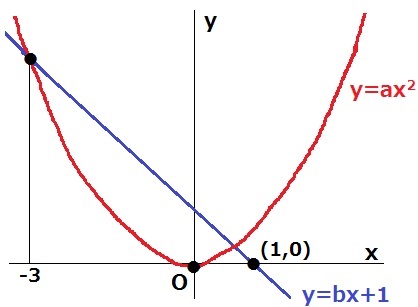
ａ＞０から、ｙ＝ａｘ²は下に凸のグラフ。
ｂ＜０から、ｙ＝ｂｘ＋１は右下の一次関数。
ｘの変域よりグラフは原点を通過し、かつ下に凸なので、まず最小値ｙ＝０が確定する。（ｃ＝０）
ｙ＝ｂｘ＋１はｘ＝１のときにｙ＝０
（１、０）を代入して、０＝ｂ＋１
ｂ＝－１

最大値はｘ＝－３のとき。
ｙ＝－ｘ＋１にｘ＝－３を代入、ｙ＝４（ｄ＝４）
最後にｙ＝ａｘ²に（－３、４）を代入して、
４＝９ａ
ａ＝４/９
ａ＝４/９、ｂ＝－１

（５）　60.0％
ｎ≦√ｘ≦ｎ＋１　←２乗する
ｎ²≦ｘ≦（ｎ＋１）²
ある平方数ｎ²から次の平方数（ｎ＋１）²までの差は100－１＝99
（*ｘはｎ²を含むので－１すること！４と９の差は５だが、４を含むと６になる）
（ｎ＋１）²－ｎ²
＝２ｎ＋１＝99
ｎ＝49

（６）　70.0％
『ａとｂの最大公約数が１』→ａとｂは共通の約数を持たない（互いに素）
ａ＋ｂ＝偶数となる場合を考える。
和が偶数となるのは（偶数＋偶数）か（奇数＋奇数）
ａとｂがともに偶数の場合、公約数２から互いに素ではない。
ａとｂがともに奇数の場合に絞られる。

『ａとｂが互いに素でない場合、√（２ａｂ）』
√（２ａｂ）が偶数となるには、ａｂ＝２×（平方数）
これらを踏まえて、ａで場合分けをする。
●ａ＝１
ｂは奇数の５、７。
●ａ＝２
ｂ＝４のとき、ａｂ＝２×４
●ａ＝３
ｂは奇数の５と７。
さらに、ｂ＝６のとき、ａｂ＝３×６＝２×９
●ａ＝４
ｂ＝８のとき、ａｂ＝４×８＝２×16
以上、７通り。
全体は４×５＝20通りだから、確率は７/20。

（７）　52.2％
ａの十の位をｘ、一の位をｙとする。
ａ＝10ｘ＋ｙ
ｂ＝10ｙ＋ｘ
（ｂ＞ａなのでｙ＞ｘ。ｘ、ｙ≠０）
ｂ＋ａ
＝（10ｙ＋ｘ）＋（10ｘ＋ｙ）
＝11（ｙ＋ｘ）
ｂ－ａ
＝（10ｙ＋ｘ）－（10ｘ＋ｙ）
＝９（ｙ－ｘ）

（ｂ²－ａ²）/99
＝（ｂ＋ａ）（ｂ－ａ）/99
＝11（ｙ＋ｘ）９（ｙ－ｘ）/99
＝（ｙ＋ｘ）（ｙ－ｘ）＝24

ｙ＋ｘ＞ｙ－ｘだから、
（ｙ＋ｘ、ｙ－ｘ）の組み合わせは、24×１、12×２、８×３、６×４。
ｙ＋ｘはいずれも偶数（24、12、８、６）なので、
ｘとｙは偶数同士か奇数同士⇒ｙ－ｘの差も偶数である。
12×２と６×４に絞られる。

ｙ＋ｘ＝12
ｙ－ｘ＝２
連立を解くと、ｘ＝５、ｙ＝７

ｙ＋ｘ＝６
ｙ－ｘ＝４
連立を解くと、ｘ＝１、ｙ＝５
したがって、ａ＝10ｘ＋ｙ＝15、57

（８）　62.1％
答案では求め方も説明する。

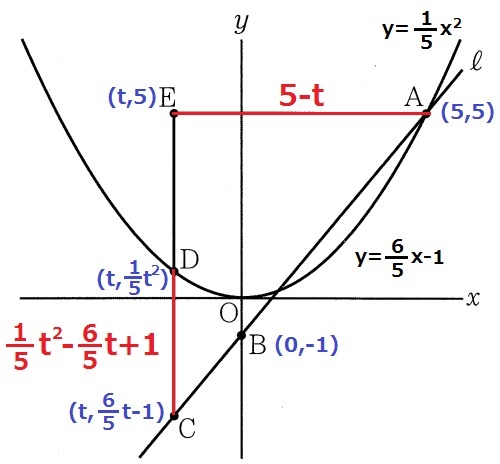
ｙ＝１/５ｘ²にｘ＝５を代入、Ａ（５、５）
ＡＢの式を求める。
Ｂから右に５、上に６移動してＡだから傾きは６/５→ｙ＝６/５ｘ－１
これにｘ＝ｔを代入、Ｃ（ｔ、６/５ｔ－１）
ｙ＝１/５ｘ²にｘ＝ｔを代入、Ｄ（ｔ、１/５ｔ²）
ＤＣ＝１/５ｔ²－（６/５ｔ－１）＝１/５ｔ²－６/５ｔ＋１
Ｅ（ｔ、５）だから、ＥＡ＝５－ｔ

１/５ｔ²－６/５ｔ＋１＝５－ｔ－３
１/５ｔ²－１/５ｔ－１＝０　←５倍
ｔ²－ｔ－５＝０
解の公式を適用。ｔ＜０より、ｔ＝（１－√21）/２

大問２（平面図形）

（１）①　83.3％
菱形の面積は〔対角線×対角線÷２〕
ａ×ＢＤ÷２＝Ｓ
ＢＤ＝２Ｓ/ａ

②　63.2％
△ＤＨＥ∽△ＢＦＥの証明。

共通角より、∠ＤＥＨ＝∠ＢＥＦ　…①
∠ＤＨＥがあけすけに垂直に見える…。
ＨはＣＨ＝ＢＧに由来する点なので、
これらを１辺とする△ＤＣＨと△ＣＢＧの関係に着目する。
仮定のＣＨ＝ＢＧ
菱形ＡＢＣＤの辺から、ＤＣ＝ＣＢ
ＡＢ//ＤＣの同位角で、∠ＤＣＨ＝∠ＣＢＧ
２辺とあいだの角が等しく、△ＤＣＨ≡△ＣＢＧ
対応する角より、∠ＤＨＣ＝∠ＣＧＢ＝90°
∠ＤＨＥ＝∠ＢＦＥ＝90°　…②
①、②より、２角相等で∽。

（２）①　67.2％

ＦＥは△ＢＦＥの１辺。
前問の△ＤＨＥ∽△ＢＦＥが使えないかを疑う。
ＢＥに対応するＤＥさえわかれば、相似比からＦＥが求まる。

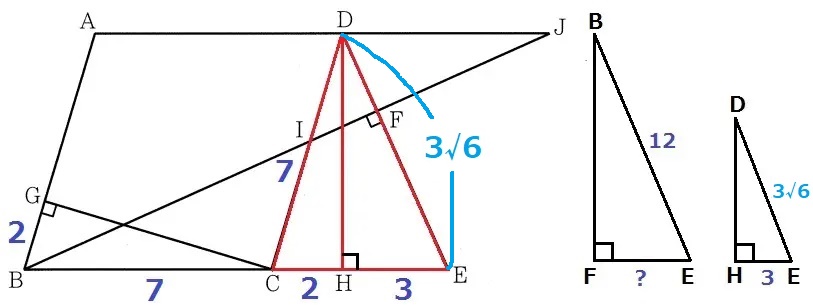
上の部分に注目する。
三平方の定理から、ＤＣ²－ＣＨ²＝ＤＨ²＝ＤＥ²－ＨＥ²
49－４＝ＤＥ²－９
ＤＥ＞０より、ＤＥ＝３√６ｃｍ
△ＤＨＥ∽△ＢＦＥで、ＦＥ＝３×12/３√６＝２√６ｃｍ

②　22.2％！

ＤＦ＝３√６－２√６＝√６ｃｍ
△ＢＥＦ∽△ＪＤＦの相似比はＥＦ：ＦＤ＝２：１なので、ＤＪ＝12÷２＝６ｃｍ
△ＪＤＦで三平方→ＦＪ＝√30ｃｍ
ＢＦ：ＦＪ＝②：①だから、ＢＪ＝√30×③＝３√30ｃｍ

△ＢＣＩ∽△ＪＤＩより、ＩＪ＝３√30×⑥/⑬＝18√30/13ｃｍ

大問３（空間図形）

（１）①　45.6％

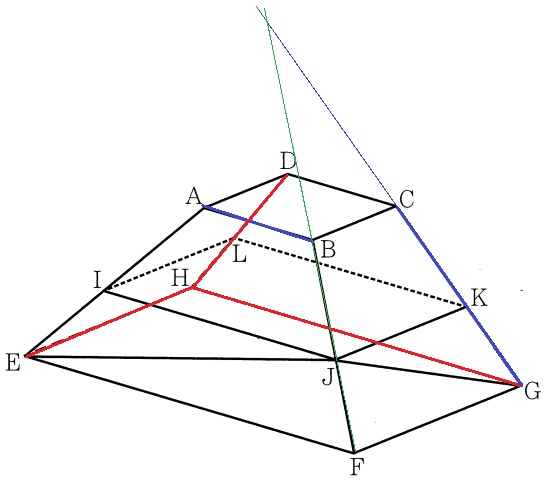
ねじれの位置…延長しても交わらない、かつ平行でもない。
ＡＢとＢＦはＢで交わる。延長するとＣＧとＢＦは上で交わる。
ネジレはＥＨ、ＧＨ、ＤＨ。
イ・エ・オ

②　6.7％!!

２/３倍と答えたくなるが、２つの台形を展開図に直してみよう。
ＥＦとＧＦは一直線ではない！
また、∠ＢＦＥと∠ＢＦＧは異なる角度なので、
ＪＦを底辺とみてもＥＦとＧＦは高さの比にならない！

△ＪＥＦと△ＪＦＧの底辺をＥＦ、ＦＧとして、
ＪをＢに移動させた△ＢＥＦ、△ＢＦＧで捉えると、
高さの比ＪＦ：ＢＦより、△ＪＥＦ：△ＪＦＧ＝△ＢＥＦ：△ＢＦＧ
△ＢＥＦ：△ＢＦＧを求めればいい。

ＢＦ＝４ｃｍ
四角形ＡＥＦＢと四角形ＢＦＧＣは等脚台形で左右対称。
お馴染みの方法で高さを出すと、２√３ｃｍと√15ｃｍ。
△ＢＥＦ：△ＢＦＧ＝６×２√３：４√15＝３：√５
△ＪＦＧは△ＪＥＦの√５/３倍。

③　18.9％！

ここも等脚台形で考える。
ＩＪ＋ＪＫは長方形ＩＪＫＬの半周だから15/２ｃｍ。

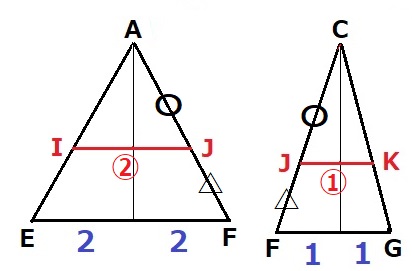
２ｃｍの真ん中を削除して、左右の三角形を合わせる。（頂点は便宜上Ａ、Ｃにした）
ＩＪ＋ＪＫ＝15/２－２×２＝７/２ｃｍ
２つの三角形は合同でも相似でもないが、〇と△が共通辺だから、
△ＡＩＪ：△ＡＥＦ＝〇：（〇＋△）＝△ＣＪＫ：△ＣＦＧ
ＩＪ：ＥＦ＝ＪＫ：ＦＧ
ＥＦ：ＦＧ＝２：１だから、ＩＪ：ＪＫ＝②：①
ＪＫ＝７/２×①/③＝７/６ｃｍ
最後に消した２ｃｍを足して、７/６＋２=19/６ｃｍ

＠別解＠

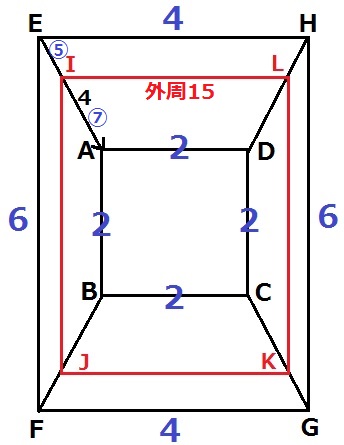
上から図形を眺めてみる。
長方形ＥＦＧＨの外周は20ｃｍ。正方形ＡＢＣＤの外周は８ｃｍ。

頂点Ｅ→Ｉ→Ａの順で外周の変化を追うと、【20ｃｍ→15ｃｍ→８ｃｍ】
上下の台形と左右の台形は異なるが、それぞれの４辺は平行なので減少率は一定。
外周の変化率からＥＩ＝⑤とするとＩＡ＝⑦になる。
ＩＡ＝４×⑦/⑫＝７/３ｃｍ

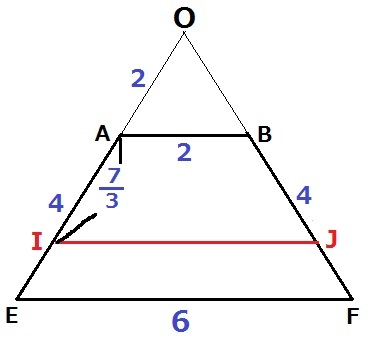
台形ＡＥＦＢにおいて、ＥＡ、ＦＢを延長した交点をＯとすると、
辺の比から△ＯＥＦは１辺６ｃｍの正三角形である。
△ＯＩＪも正三角形で、ＯＩ＝ＩＪ＝２＋７/３＝13/３ｃｍ
ＩＪ＋ＪＫが15/２ｃｍだから、ＪＫ＝15/２－13/３＝19/６ｃｍ

（２）①　42.2％

（１）②の図が使える。
Ｂから垂線をひき、ＥＦ、ＦＧとの交点をそれぞれＰ、Ｑとする。
ＢＰ＝２√３ｃｍ、ＦＱ＝ＰＭ＝１ｃｍ
△ＢＰＭで三平方→ＢＭ＝√11ｃｍ

②　4.4％!!

求めるべき立体を面ＡＮＯＤで分割する。
立体ＡＤ―ＥＮＯＨと立体ＮＯ―ＡＢＣＤを断頭三角柱で求積するのが良いと思う。

ＡＤ、ＢＣ、ＥＨ、ＮＯの中点をそれぞれＲ、Ｓ、Ｔ、Ｕとする。
立体ＡＤ―ＥＮＯＨ…底面積は対称面の△ＲＴＵ、高さはＡＤ、ＥＨ、ＮＯの平均。
立体ＮＯ―ＡＢＣＤ…底面積は対称面の△ＲＵＳ、高さはＡＤ、ＢＣ、ＮＯの平均。

３×√11÷２×（２＋４＋４）/３＋２×√11÷２×（２＋２＋４）/３
＝５√11＋８√11/３
＝23√11/３ｃｍ³

2023年度・大阪（数学）Ａ問題、Ｂ問題の解説はコチラ。
公立高校入試解説ページに戻る