2019年度　海城中学過去問【算数】大問４解説

問題ＰＤＦ
（１）
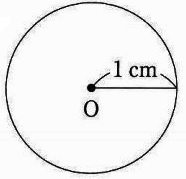
図のように、１辺の長さが６ｃｍの正方形ＡＢＣＤがあります。辺ＡＢ、ＢＣ、ＣＤ、ＤＡの真ん中の点をそれぞれＥ、Ｆ、Ｇ、Ｈとします。半径１ｃｍの円Ｐの中心は、ＡＢ、ＢＣ、ＣＤ、ＤＡ、ＥＧ、ＨＦの上をすべて動きます。このとき円Ｐの円周が通った部分の面積を求めなさい。

（２）
図のように、半径１ｃｍの円Ｏがあります。半径５ｃｍの円Ｑの中心は、円Ｏの内部と周上をすべて動きます。
このとき、円Ｑの円周が通った部分の面積を求めなさい。

＠解説＠
（１）

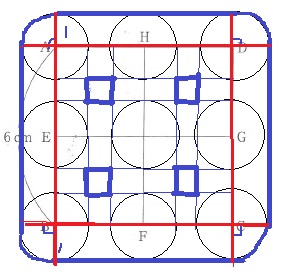
９ヶ所に円を描き、軌跡を作図する。
すると、１ｃｍ四方の小窓が４つある。

中にある６ｃｍの正方形から４つの小窓をひく。
外側は１×６の長方形が４箇所、四隅は１つに統合すると半径１ｃｍの円。
６×６－１×１×４＋１×６×４＋１×１×3.14＝59.14ｃｍ²

（２）
半径５ｃｍのＱが、半径１ｃｍの円Ｏの円周と内部を動く。

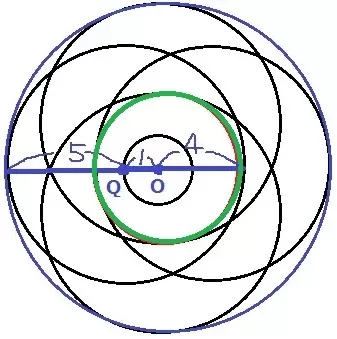
気をつけるべき点は、内側に円Ｑの円周が通らないスペースがあること！
求積すべきところは、半径６ｃｍの青い円から半径４ｃｍの赤い円の間。
６×６×3.14－４×４×3.14
＝（36－16）×3.14
＝20×3.14＝62.8ｃｍ²

＠別解＠

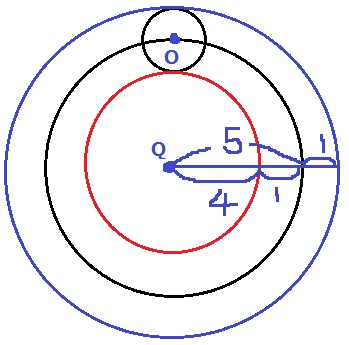
もしくは、円Ｑを固定して円Ｏを動かすこともできる。
（円Ｏを固定して円Ｑを動かす＝円Ｑを固定して円Ｏを動かす）
こちらの方が作図がしやすい。
半径６ｃｍの円から半径４ｃｍの円をひくので、先ほどと同様の式になる。
難関中（算数科）解説ページに戻る