2024年度　岡山県公立高校入試問題過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
５＋（－12）
＝５－12
＝－７

（２）
７－８×（－２）
＝７＋16
＝23

（３）
２/３ａｂ÷（－４ｂ）×９ａ
＝－３/２ａ²

（４）
（√３－√５）²
＝３－２√15＋５
＝８－２√15

（５）
ｘ＋５ｙ＝11　…①
３ｘ＋２ｙ＝－６　…②
①×３－②をすると、13ｙ＝39
ｙ＝３
①に代入、ｘ＋15＝11
ｘ＝－４
ｘ＝－４、ｙ＝３

（６）
ｘ（ｘ＋２）＝48
ｘ²＋２ｘ－48
＝（ｘ＋８）（ｘ－６）＝０
ｘ＝－８、６

（７）
ｙ＝ｘ－５にｘ＝－２を代入→Ａ（－２、－７）
これをｙ＝ａｘ²に代入する。
－７＝４ａ
ａ＝－７/４

（８）
３枚のうち１枚が表になる出方→３通り
全体は２³＝８通りで、確率は３/８。

（９）

Ｖ：Ｗ
＝３×３×π×４÷３：４×４×π×３÷３
＝３：４

（10）

平行四辺形の対角から、∠Ａ＝∠Ｃ
折り返しで∠Ｃ＝∠Ｅだから、∠Ａ＝∠Ｅ
２点Ａ、Ｅは直線ＢＤについて同じ側にあって、∠Ａ＝∠Ｅだから、
円周角の定理の逆より４点Ａ、Ｂ、Ｄ、Ｅは一つの円周上にある。

大問２（データの活用）

（１）
全数調査は調査対象すべてを調べ上げる。
標本調査は母集団のなかから標本を無作為に抽出して、母集団の様子を推し量る。
理由が選択肢に述べられているので選びやすい。
健康診断と国勢調査が全数調査、品質管理と視聴率調査が標本調査。
イ・ウ

（２）①

標本の選び方。母集団である全校生徒300人から無作為（ランダム）に抽出する必要がある。
Ｘ：通し番号をつけるのは問題ない。乱数表は数字がランダムに羅列した表で、標本の抽出に役立つ。〇
　実際は乱数を生成するアプリを使うのが楽です。
Ｙ：１年生に限定している。×
Ｚ：アンケートの回答者に限定している。×
ア

②
解答欄には式も書く。
抽出した50人のうち、数学好きは28人。
この割合は母集団300人も同じとみなし、数学好きは300×28/50＝168人

（３）

範囲＝最大値－最小値
四分位範囲＝第３四分位数（Q3）－第１四分位数（Q1）
標本の大きさが大きいほど、範囲や四分位範囲が小さい傾向にある。
→サンプルが多いほど、バラツキが少なくなる。
イ

大問３（整数）

（１）
【仮定】６以上31以下の自然数ｍが６の倍数→【結論】ｍ－１とｍ＋１はどちらも素数。
この命題が成り立たない反例を挙げる。

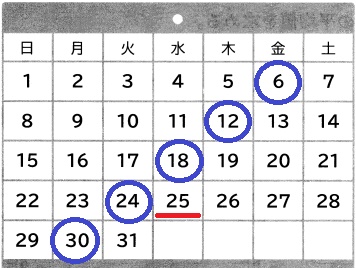
カレンダーの６の倍数に印をつけると見つけやすい。
25は素数ではない。
（例）ｍ＝24のとき

（２）
（あ）偶数の素数は２しかない。２以外の偶数は２で割れるので素数ではない。
よって、２より大きい素数は奇数。
（い）ｎ－１とｎ＋１が素数＝奇数→ｎは偶数。
ウ

（３）①
ａ÷３＝ｂ…１
ａ＝３ｂ＋１→ａ－３ｂ＝１、ａ＞３ｂ
イ・エ

②
連続する３つの整数は、３で割った余りが【０→１→２…】でループする。
ａ÷３の余りが１
（ａ＋１）÷３の余りは２
（ａ＋２）÷３の余りは０

（４）
32以上のある自然数の前後が素数である。
前問を手掛かりにするが、問題文の後半にヒントがある。

素数は奇数。連続する３つの整数のうち、素数は３の倍数ではない。
→真ん中の数は２の倍数かつ３の倍数、すなわち、６の倍数。
32以上の６の倍数で、前後が素数であるものを書けばいい。
（例）42、60、72、102など

＠余談＠
（３・５）のように、差が２である素数のペアを双子素数という。
（３・５）以外の双子素数はあいだの数が６の倍数で、〔６の倍数－１〕と〔６の倍数＋１〕のペアになる。
双子素数が無限個あるかどうかは、未だ証明されていない。

（１）の命題【６以上の自然数ｍが６の倍数→前後はいずれも素数】は反例があったが、
逆の【６以上の自然数ｍの前後がいずれも素数→ｍは６の倍数】は必ず成り立つ。

大問４（関数）

（１）
ｙがｘの関数である→ｘの値を決めれば、それに伴ってｙの値もただ１つに決まる関係。
ア：時間＝道のり÷速さ。ｙ＝10000/ｘ
イ：たとえば、周の長さが12ｃｍの場合、縦＋横＝６ｃｍ
面積は１×５＝５ｃｍ²、２×４＝８ｃｍ²など１つに決まらない。×
ウ：ｙ＝1500－10ｘ（ｙ＝－10ｘ＋1500）
エ：ｙ＝πｘ²
ア・ウ・エ

（２）①

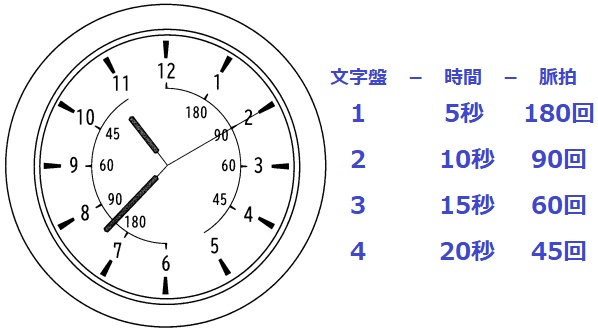
文字盤と時間、脈拍の関係性を書き出してみる。
時間（ｘ）が経つほど１分間の脈拍（ｙ）は減っている。
時間が２倍になると脈拍は半分だから、反比例のグラフになる。
ウ

②
反比例の比例定数ａ＝10×90＝900
ｙ＝900/ｘ
ｘ＝15のとき、最小値ｙ＝60
最大値ｙ＝100を代入して、ｘ＝９

（３）
文字盤３だけを見る。
先ほどの時計では【15秒で15回】→60秒で60回（ｘ＝15、ｙ＝60）
今度は【15秒で20回】だから１分間の脈拍は、20×60/15＝80回

＠余談＠
計測時間を固定すると、計測する脈拍数と１分間あたりの脈拍数は比例にある。
15回の計測で１分間の脈拍は60回→20回の計測では、60×20/15＝80回と求められる。

大問５（平面図形）

（１）
Ａを中心として垂線ｈを時計回りに30°回転移動した直線ｎを作図する。
直線ｎは右上の線で、垂線ｈとなす角が30°である。

ℓとｈの交点をＯとする。
①ＡＯを１辺とする正三角形をつくる。残りの頂点をＰとする。
②∠ＰＡＯの二等分線で30°がつくれる。この二等分線が直線ｎ。

（２）
△ＡＨＤ≡△ＡＩＥの証明。

正三角形ＡＤＥ、ＡＨＩの１辺からＡＤ＝ＡＥ、ＡＨ＝ＡＩ
∠ＨＡＤ＝60－∠ＤＡＩ＝∠ＩＡＥ
２辺とあいだの角が等しいので合同。

（３）

同様に、△ＡＦＨ≡△ＡＧＩだから、
∠ＡＨＦ＝∠ＡＩＧ＝180－60＝120°

＠別解＠
前の△ＡＨＤ≡△ＡＩＥより、∠ＡＨＤ＝∠ＡＩＥ＝60°から導いてもよい。

（４）

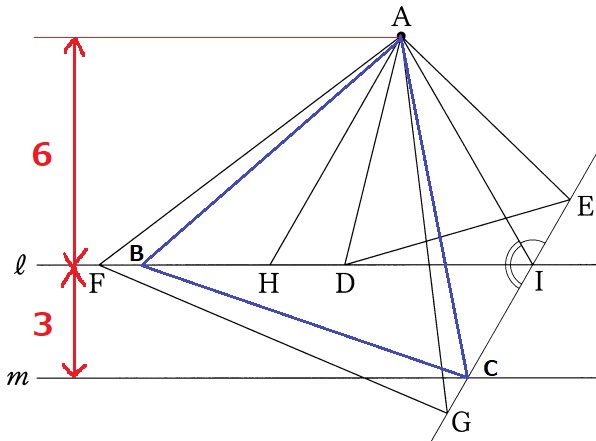
正三角形ＡＢＣをつくる。この１辺の長さを求めるが、
わかっているのが６ｃｍと３ｃｍしかない。

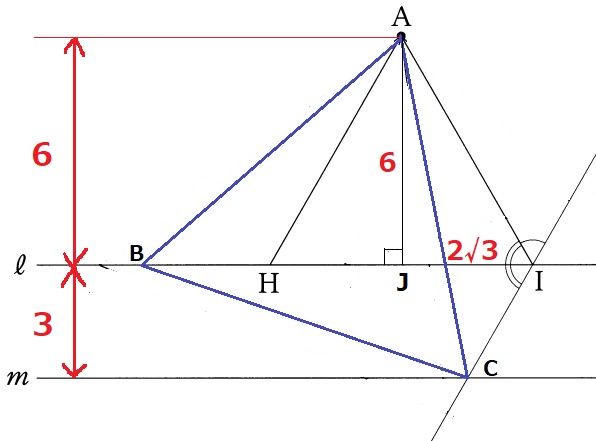
↑邪魔な正三角形を削除した。
直線ℓに接する△ＡＨＩは使えるので残す。
Ａから垂線ひいて足をＪとすると、ＪＩ＝６×１/√３＝２√３ｃｍ

情報が足りないので、ＡＪとＩＣを延長した交点をＬとし、ＡＬを１辺とする正三角形ＡＫＬを作る。
Ｋは直線ℓ上にあるので、ＫＪ⊥ＡＬからＪはＡＬの中点である。
ＡＪ＝ＪＬ＝６ｃｍ

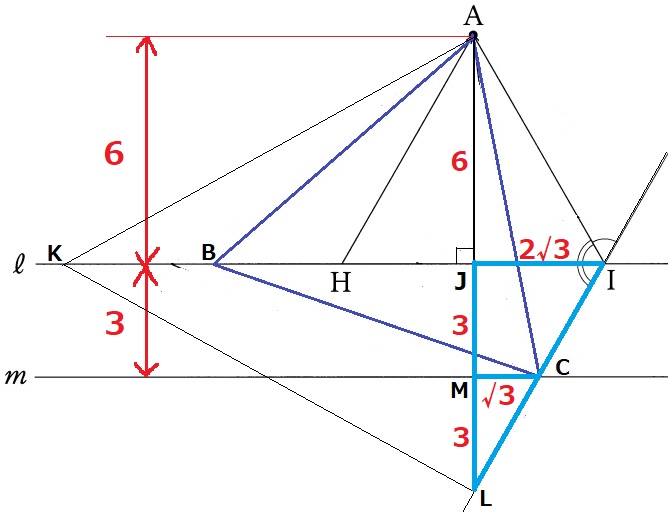
ＪＬと直線ｍの交点をＭとする。
ＪＭ＝ＭＬ＝３ｃｍ
△ＪＩＬ∽△ＭＣＬより、ＭＣ＝２√３÷２＝√３ｃｍ
△ＡＣＭで三平方→ＡＣ＝２√21ｃｍ