2023年度　宮城県公立高校入試問題過去問【数学】解説

平均45.6点（前年比；－12.6点）
最高点100点、最低点０点
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
－９＋２
＝－７

（２）
－15÷（－５/３）
＝－15×（－３/５）
＝９

（３）
110＝２×５×11

（４）
４ａ－９ｂ＋３＝０
４ａ＝９ｂ－３
ａ＝９/４ｂ－３/４

（５）
３ｘ－ｙ＝17　…①
２ｘ－３ｙ＝30　…②
①×３－②をすると、７ｘ＝21
ｘ＝３
①に代入、３×３－ｙ＝17
ｙ＝－８
ｘ＝３、ｙ＝－８

（６）
√54＋12/√６
＝３√６＋２√６
＝５√６

（７）
ｙ＝２/３ｘにｘ＝６を代入。
ｙ＝２/３×６＝４
ｙ＝ａ/ｘにＡ（６、４）を代入。
ａ＝６×４＝24

（８）
ア：第１四分位数はＡ組が３冊、Ｂ組が４冊。×
イ：四分位範囲＝第３四分位数－第１四分位数
　箱の横の長さで、最も小さいのはＢ組。×
ウ：35人の中央値（第２四分位数）は18番目の値。
　Ｂ組は少なくとも18人が６冊以上で最も多い。〇
エ：最小値２、最大値８のＡは、すべて２～８冊の範囲内にある。×
　Ｃの２～８冊は、中央値の前後にあつまる全データの50％ほど。
ウ

大問２（小問集合２）

（１）①
４×２×π×１/３＝８/３πｃｍ

②

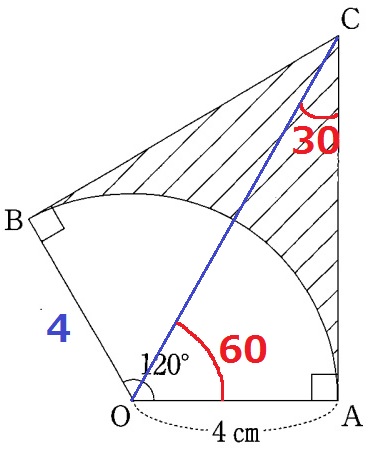
ＯＣに補助線。
共通辺ＯＣ、半径ＯＢ＝ＯＡ、∠ＯＢＣ＝∠ＯＡＣ＝90°より、
斜辺と他の１辺が等しく、△ＯＢＣ≡△ＯＡＣ

∠ＣＯＡ＝120÷２＝60°
△ＯＡＣの内角から辺の比は１：２：√３→ＣＡ＝４√３ｃｍ
求積すべき部分は、四角形ＯＡＣＢから扇形をひく。
４×４√３÷２×２－４×４×π×１/３
＝16√３－16/３πｃｍ²

（２）①
ｙ＝ａｘ²において、ｘの値がｐ⇒ｑに増加したときの変化の割合はａ（ｐ＋ｑ）。
１/４×（０＋６）＝３/２

②

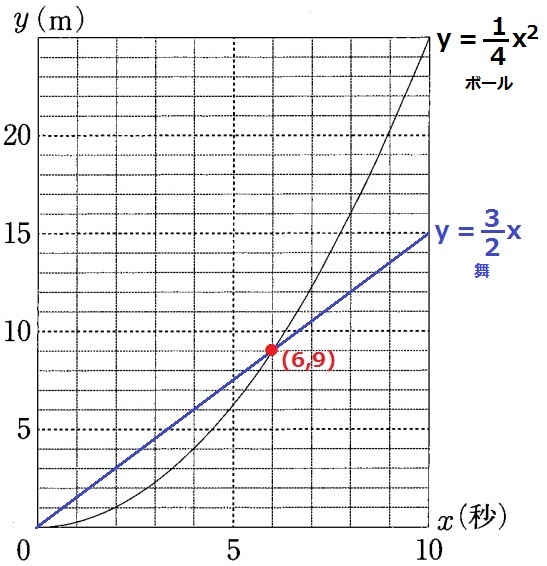
ｙ＝１/４ｘ²にｘ＝６を代入。
ｙ＝１/４×６²＝９
（６、９）の点でボールと舞のグラフが交わる。
舞の傾きは９/６＝３/２→ｙ＝３/２ｘ

ボールが舞を追い越した後、あいだの距離が18ｍになった。（ｙ座標の差が18になった）
１/４ｘ²－３/２ｘ＝18
ｘ²－６ｘ－72
＝（ｘ＋６）（ｘ－12）＝０
ｘ＞０より、ｘ＝12
12秒後

（３）

最初は、赤：白＝④：①だった。
白を300個追加すると、取り出した120個のなかでは赤80個、白40個だから、
赤：白＝80：40＝②：①になった。

赤球の個数が変わっていないことに注目すると④＝②
〇を２倍して〇に統一すると、白の②－①＝①が追加した300個にあたる。
最初の赤は、300×④＝1200個

（３）①
45÷３＝15
→45は15行目の最大数。
奇数行は３列目が最も大きいので、15行目の３列目。

②ア
各行の最大数を拾い上げると…
１行目―３、２行目―６、３行目―９、…ｎ行目―３ｎ
ｎ行目の最小数は最大数－２。
３ｎ－２

イ
ｎ行目の最小数Ｐ＝３ｎ－２
１つ手前のｎ－１行目の最大数ＱはＰ－１である。
Ｑ＝３ｎ－３

Ｐ＋Ｑ
＝（３ｎ－２）＋（３ｎ－３）
＝６ｎ－５＝349
ｎ＝59
59行目は奇数行で、３列目は最大数。
ｎ行目の最大数は３ｎだから、３×59＝177

大問３（総合問題）

（１）①

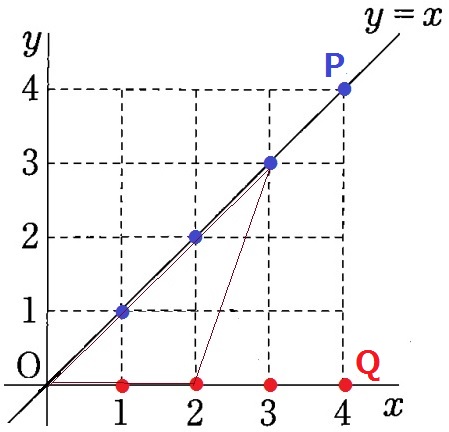
ＰとＱの位置を確認。
問題文に『合同な三角形の組はない』とあるように、△ＯＰＱの形が重複しない。
△ＯＰＱは全部で４×４＝16通り

②

∠ＰＯＱ＝45°は固定。
∠ＰＱＯ＝90°（斜辺ＯＰ）が４通り。
∠ＯＰＱ＝90°（斜辺ＯＱ）が２通り。
計６通り、確率は６/16＝３/８

（２）①

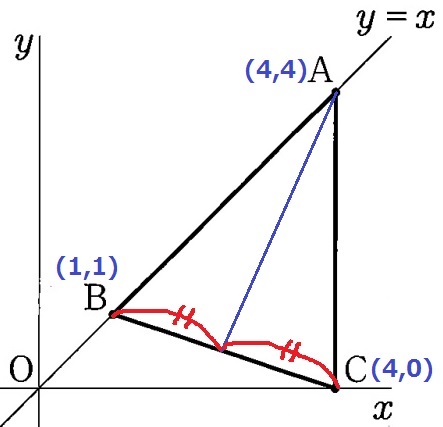
ＢＣの中点を通過する直線で△ＡＢＣが２等分される。
エ

②
Ｂ（１、１）→Ｃ（４、０）
右に３、下に１だから、傾きは－１/３。
Ｂから左に１、上に１/３で、切片は１＋１/３＝４/３
ｙ＝－１/３ｘ＋４/３

③

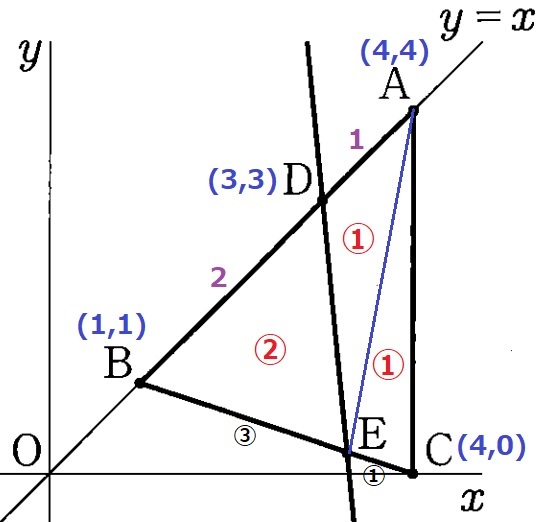
ＡＥに補助線をいれる。
ＢＤ：ＤＡ＝２：１より、△ＤＢＥ：△ＡＤＥ＝②：①
△ＤＢＥ＝四角形ＤＥＣＡ＝②だから、△ＡＥＣ＝②－①＝①
△ＡＢＥ：△ＡＥＣ＝ＢＥ：ＥＣ＝③：①

ＥはＢＣを③：①に内分する点。
内分点の公式からＥのｘ座標は、（①×１＋③×４）/（③＋①）＝13/４
（もしくは、ＢとＣのｘ座標の差３を３/４倍してＢの１を足す）
ｙ座標はＢの１/４だから１/４。
Ｅ（13/４、１/４）

大問４（平面図形）

（１）
△ＣＤＥ∽△ＢＦＥの証明。

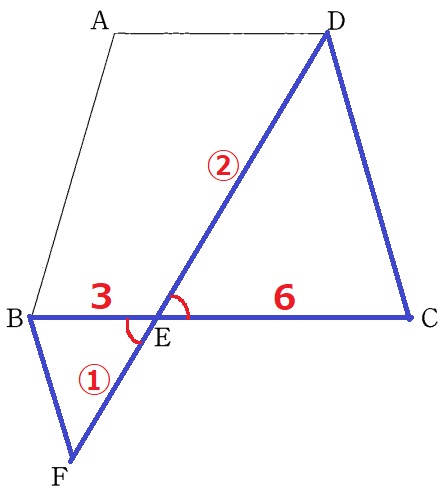
対頂角は見えるが、もう１つの等角がなかなか出てこない(;´･ω･)
辺の情報に切り替える。
ＥＣ＝９－３＝６ｃｍ→ＣＥ：ＢＥ＝２：１
ＤＥ：ＦＥ＝ＣＥ：ＢＥ
２辺の比とあいだの角が等しいから∽。

（２）
△ＣＤＥ：△ＢＦＥの相似比は２：１。
ＣＤ＝７ｃｍだから、これに対応するＢＦ＝７/２ｃｍ

（３）①

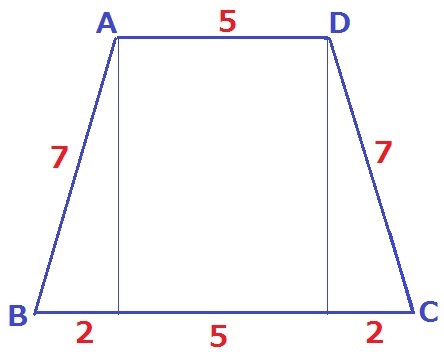
四角形ＡＢＣＤは等脚台形で左右対称。
垂線をおろし、下底の両端の長さは（９－５）÷２＝２ｃｍ
三平方の定理を用いて、高さは３√５ｃｍ。

②

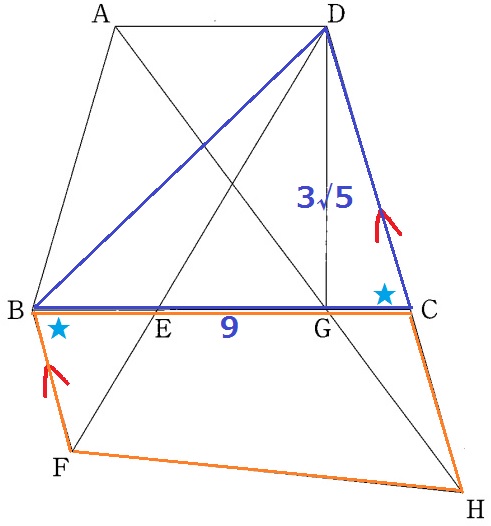
前問の解答から、△ＤＢＣの面積は９×３√５÷２＝27√５/２ｃｍ²
（１）△ＣＤＥ∽△ＢＦＥの対応する角（★）から錯角が等しい→ＢＦ//ＤＨ
台形ＢＦＨＤの上底と下底から、△ＤＢＣ：四角形ＢＦＨＣ＝ＤＣ：（ＢＦ＋ＣＨ）

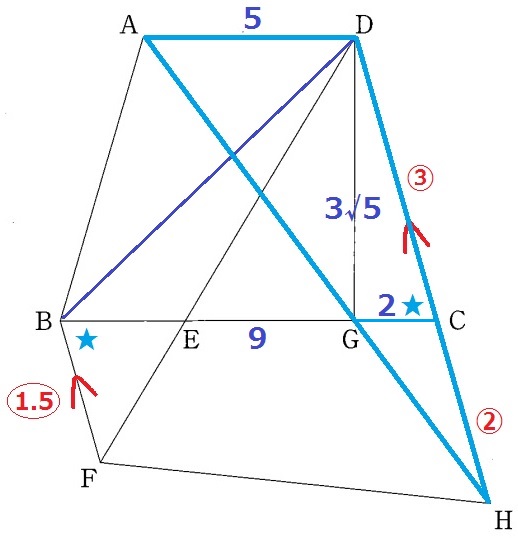
ＧＣは前問で２ｃｍと求めている。
△ＡＨＤ∽△ＧＨＣの相似比は、ＡＤ：ＧＣ＝５：２
ＤＣ＝③、ＣＨ＝②とする。
（１）△ＣＤＥ∽△ＢＦＥより、ＢＦ＝③÷２＝〇1.5
ＤＣ：（ＢＦ＋ＣＨ）＝③：（〇1.5＋②）＝③：〇3.5
四角形ＢＦＨＣの面積は、27√５/２×〇3.5/③＝63√５/４ｃｍ²