2022年度　宮城県公立高校入試問題過去問【数学】解説

平均58.2点（前年比；＋10.6点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
－７－４
＝－11

（２）
６＋（－２）²
＝６＋４
＝10

（３）
３ｘｙ²÷15ｘｙ
＝１/５ｙ

（４）
（ａ＋４ｂ）－（２ａ－ｂ）
＝ａ＋４ｂ－２ａ＋ｂ
＝－ａ＋５ｂ　←ここで代入
＝－（－１）＋５×３/５
＝１＋３＝４

（５）
√３×√６－√２
＝３√２－√２
＝２√２

（６）
ｘ²－ｘ－12
＝（ｘ＋３）（ｘ－４）＝０
ｘ＝－３、４

（７）
反比例の比例定数ａはｘとｙの積。
ｙ＝－10/ｘ
これにｘ＝３を代入して、ｙ＝－10/３

（８）

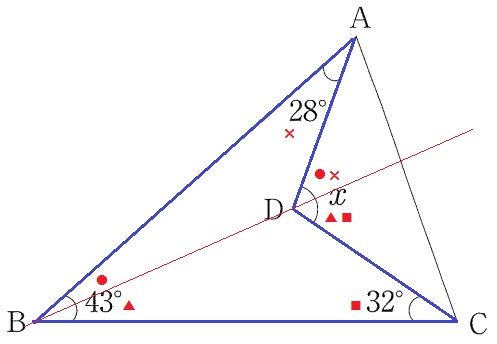
『ブーメランの３つの角の和は股の角』
上下で外角定理を使い、ｘ＝43＋28＋32＝103°

大問２（小問集合２）

（１）①
Ｂ（２、－４）をｙ軸について対称移動させる。
Ｃ（－２、－４）

②

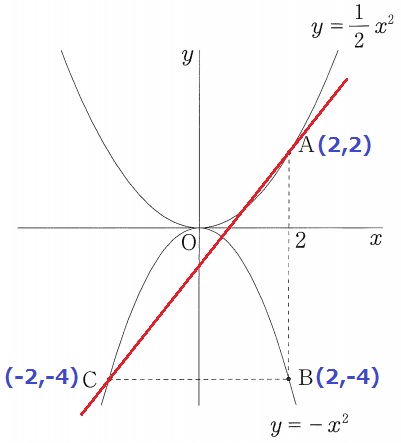
Ｃ（－２、－４）⇒Ａ（２、２）
右に４、上に６だから、傾きは６/４＝３/２
Ｃから右に２、上に３移動して、切片は－４＋３＝－１
ｙ＝３/２ｘ－１

（２）①
３×３×π×４÷３＝12πｃｍ³

②
相似比は、Ｐ：全体（三角錐）＝ＡＢ：ＡＯ＝３：５
体積比は３乗して、Ｐ：全体＝27：125
Ｑの体積比は、125－27＝98
よって、ＰとＱの体積比は、Ｐ：Ｑ＝27：98

（３）①
30％＝0.3（３/10）
カレーライスは0.3ｘ（３/10ｘ）人。

②
１年生をｘ人としたので、２年生は155－ｘ人。
0.3ｘ＋0.24（155－ｘ）＝42
30ｘ＋3720－24ｘ＝4200
６ｘ＝480
ｘ＝80

２年生は、155－80＝75人
２年生のから揚げは、75×36％＝27人

（４）①
100人の中央値（メジアン）は50番目と51番目の平均。
下から数えていくと、20ｍ以上25ｍ未満の階級。

②
ア：50人の中央値は25番目と26番目の平均。20～25ｍの階級で同じ。〇
イ：Ａの最大値は30～35、Ｂは35～40に含まれ、Ｂの方が大きい。×
ウ：Ａの最頻値（モード）はＡが17.5、Ｂが22.5でＢの方が大きい。×
エ：Ａが20/100、Ｂが6/50＝12/100で、Ａの方が大きい。〇
オ：累積相対度数は、その階級以下の度数の合計の割合。
Ａが46/100、Ｂが24/50＝48/100で、Ｂの方が大きい。×
ア・エ

大問３（確率＆数量変化）

（１）①
３×４＝12通り

②

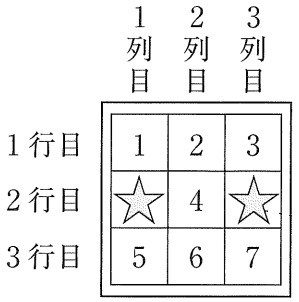
縦ラインは（１、５）（３、７）
横ラインは箱Ｂで４を出せば、箱Ａは何でもいい。３通り
斜めラインは無し。
計５通り。
確率は５/12。

（２）①
Ａは60分間で300Ｗｈだから、10分間では300÷６＝50Ｗｈ

②ア

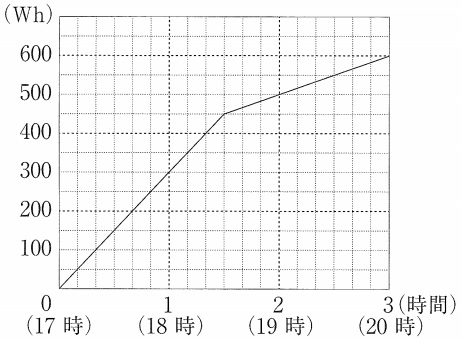
横の１マスが10分、縦が50ｋＷ。前問と同じ値である。
17時～18時30分の設定Ａは傾き１。
設定Ｂの１時間あたりの消費電力量は設定Ａの１/３倍なので、
18時30分～20時までは傾きが１/３（右に３、上に１）。

イ

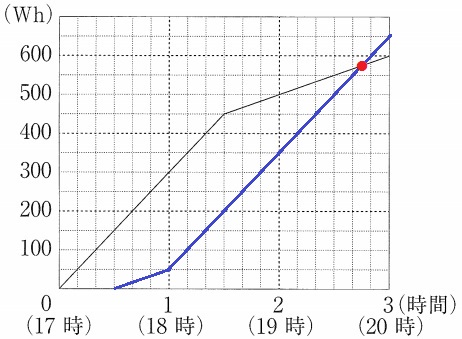
休日のグラフを描く。交点●が答え。

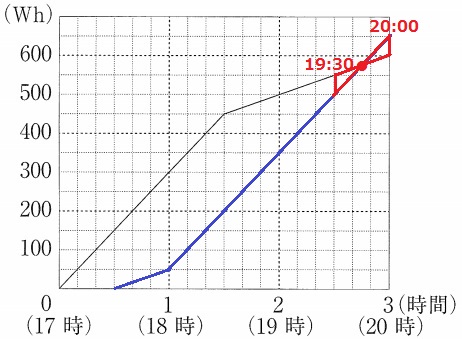
格子点を通るところを見つけて、三角形の相似。
相似比は１：１。
19時30分と20時のあいだの19時45分。

大問４（平面図形）

（１）
直径に対する円周角ＡＣＢ＝90°
△ＡＢＣで三平方→ＢＣ＝２√５ｃｍ

（２）
△ＡＢＣ∽△ＡＤＥの証明。

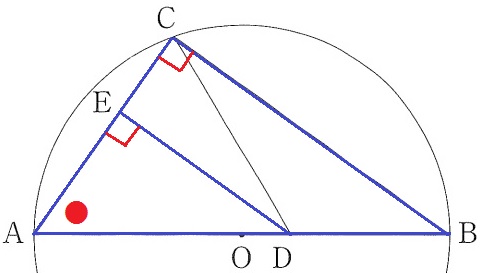
仮定より、∠ＡＥＤ＝90°
先ほどの直径に対する円周角から∠ＡＣＢ＝90°
これに共通角を合わせて、２角が等しく∽。

（３）
ＡＤ＝４ｃｍ、ＤＢ＝６－４＝２ｃｍ

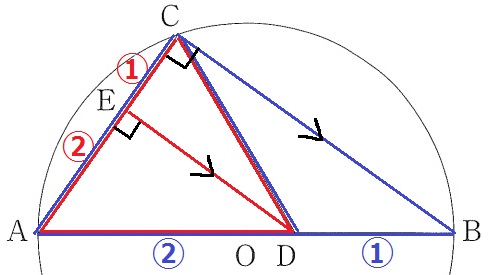
前問の相似より、ＡＤ：ＤＢ＝ＡＥ：ＥＣ＝４：２＝２：１
（∠ＡＥＤ＝∠ＡＣＢで同位角が等しい→ＥＤ//ＣＢでもＯＫ）
△ＡＢＣの面積は、４×２√５÷２＝４√５ｃｍ²
【△ＡＣＢ→△ＡＣＤ→△ＣＥＤ】
△ＣＥＤの面積は、４√５×②/③×①/③＝８√５/９ｃｍ²

（４）

ＤＧの比を求めるには、直径ＡＢより下の情報が欲しい。
下の世界の情報を得るために、△ＡＣＤ∽ＦＢＤを足掛かりにする。
ＢＤに対応する辺はＣＤなので、ＣＤの長さが知りたい。

△ＡＥＤ∽△ＡＣＢより、ＥＣ＝４×１/３＝４/３ｃｍ
ＥＤ＝２√５×２/３＝４√５/３ｃｍ
△ＣＤＥで三平方→ＣＤ＝４√６/３ｃｍ

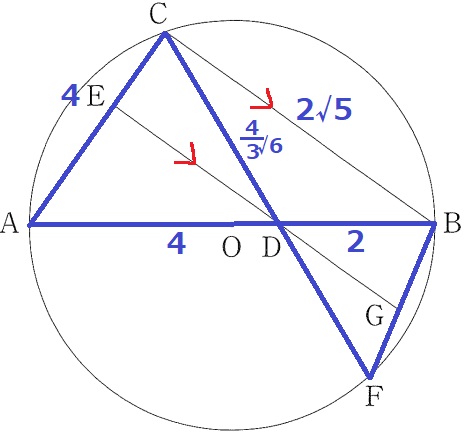
△ＡＣＤ∽ＦＢＤより、相似比はＣＤ：ＢＤ＝４√６/３：２＝２√６：３
ＤＦ＝４×３/２√６＝√６ｃｍ

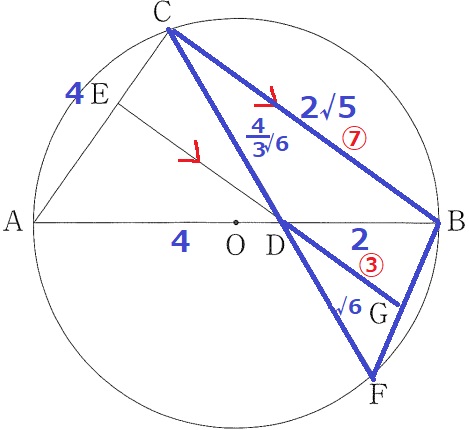
ＣＤ：ＤＦ＝４√６/３：√６＝４：３
△ＦＤＧ∽△ＦＣＢより、ＤＧ＝③とすると、ＣＢ＝⑦

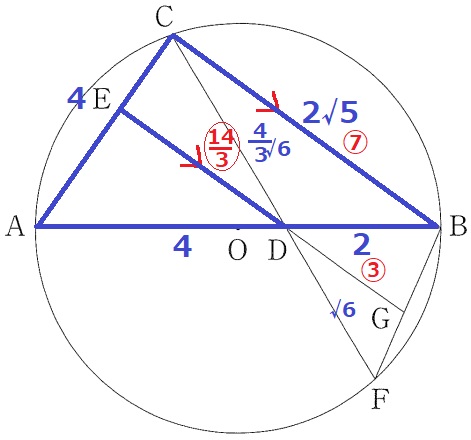
最後に△ＡＣＢ∽△ＡＥＤで、ＥＤ＝⑦×２/３＝〇14/３
したがって、ＥＤ：ＤＧ＝14/３：３＝14：９

＠余談＠
どこかで見覚えがある…と既視感にかられて探してみました。

2021年奈良の大問４（４）（正答率0.2％）がやや似た感じのルートをたどります。