2023年度　沖縄県公立高校入試問題過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）
－５－（－７）
＝－５＋７
＝２

（２）
（－12）÷４/３
＝－９

（３）
７－５×（－２）
＝７＋10
＝17

（４）
√12＋√27
＝２√３＋３√３
＝５√３

（５）
（－３ａ）²×（－２ｂ）
＝９ａ²×（－２ｂ）
＝－18ａ²ｂ

（６）
３（５ｘ＋２ｙ）－４（３ｘ－ｙ）
＝15ｘ＋６ｙ－12ｘ＋４ｙ
＝３ｘ＋10ｙ

大問２（小問集合）

（１）
５ｘ－６＝２ｘ＋３
３ｘ＝９
ｘ＝３

（２）
２ｘ＋ｙ＝５　…①
ｘ－２ｙ＝５　…②
①×２＋②をすると、５ｘ＝15
ｘ＝３
①に代入、６＋ｙ＝５
ｙ＝－１
ｘ＝３、ｙ＝－１

（３）
（ｘ＋３）（ｘ－３）
＝ｘ²－９

（４）
ｘ²＋２ｘ－15
＝（ｘ＋５）（ｘ－３）

（５）
２ｘ²＋５ｘ＋１＝０
ｘ＝（－５±√17）/４

（６）
√５＜ｎ＜√11
５＜ｎ²＜11
この範囲にある平方数は９だから、ｎ＝３

（７）

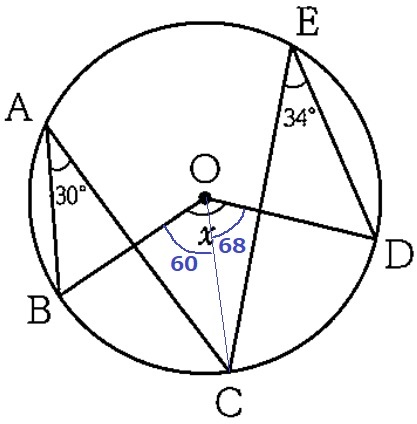
中心角は円周角の２倍。
ｘ＝（30＋34）×２＝128°

（８）
10％値上がり＝110％＝110/100
120×110/100×３＝396円

（９）
パッと見て最頻値が大きいが、ここでは一応確認しておく。
平均値…（０×１＋１×３＋２×３＋３×５＋４×６＋５×２＋６×０）÷20＝58÷20＝2.9問
中央値…20人の中央値は10番目と11番目の平均で３問。
最頻値…最もあらわれている値で４問。
ウ

大問３（データの活用）

（１）
最小値20.1℃が判断しやすいかな？
Ｂ
*Ａ…2021年、Ｂ…2022年、Ｃ…2020年、Ｄ…2019年

（２）
範囲＝最大値－最小値＝30.7－22.7＝8.0℃

（３）
ア：四分位範囲＝第３四分位数－第１四分位数
　箱ひげ図でいうと箱の横の長さで、2021年が最も大きい。×
イ：31日のQ1（第１四分位数）は下位15日の真ん中、下から８番目。
　2022年のQ1は24.4℃だから、25℃以下は少なくとも８日はある。〇
ウ：2022年の最大値は29.9℃だから、30℃超えはない。×
エ：2019年だけ平均値の方が中央値よりも大きい。×
イ

大問４（確率）

（１）
６×６＝36通り

（２）
ｎ≧55となる整数は55、56、61、62、63、64、65、66の８通り。
確率は８/36＝２/９

（３）
一の位は１～６。十の位を１とすると11～16は連続する６つの整数。
３の倍数、３の倍数＋１、３の倍数＋２が必ず２個ずつ出てくる。
これは十の位が２～６でも同じだから、３の倍数は２×６＝12個
確率は12/36＝１/３

大問５（数量変化）

（１）
通話料金：１分あたり50円→傾きは50
基本料金：０円→切片は０（比例）
ｙ＝50ｘ

（２）
60分を超えた部分の通話料金は、40円×20分＝800円
2000＋800＝2800円

（３）
●Ａプランとの関係
Ａの通話料金がＢの基本料金を超える時間は、2000÷50＝40分
40分後のＢは2000円のまま。40分を超えるとＢの方が安くなる。
●Ｃプランとの関係
Ｂの基本＋通話料金がＣの基本料金と同じになる時間を見つける。
60分のとき、料金の差は2960－2000＝960円
960÷40＝24分後にＣと料金が等しくなる。
60＋24＝84分を超えるとＣの方が安くなる。
Ｂが最も安いのは、40分から84分までの間。

大問６（整数）

（１）
結果を聞いているので、適当な値で調べてみる。
４²－２²＝12
６²－４²＝20
８²－６²＝28
いずれも４の倍数。

（２）
証明問題。問題文に従って記述すればいい。
ｎを整数とすると、連続する２つの偶数は２ｎ、２ｎ＋２と表せる。
（２ｎ＋２）²－（２ｎ）²
＝８ｎ＋４
＝４（２ｎ＋１）
２ｎ＋１が整数だから、４（２ｎ＋１）は４の倍数である。
したがって、連続する２つの偶数では、
大きい偶数の２乗から小さい偶数の２乗をひいた数は４の倍数になる。

大問７（作図）

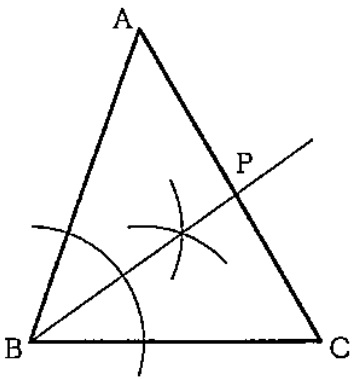
∠ＡＢＰ＝70÷２＝35°
∠Ｂの二等分線を作図すればいい。

大問８（関数）

（１）
ｙ＝ａｘ²について、
ｘ＝－２のとき、ｙ＝４ａ
ｘ＝１のとき、ｙ＝ａ
変化の割合＝（ｙの増加量）÷（ｘの増加量）＝（ａ－４ａ）÷｛１－（－２）｝
＝－ａ＝２
ａ＝－２
①…４ａ、②…－２

＠余談＠
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増えたときの変化の割合はａ（ｐ＋ｑ）。
（－２＋１）ａ＝２
ａ＝－２

（２）
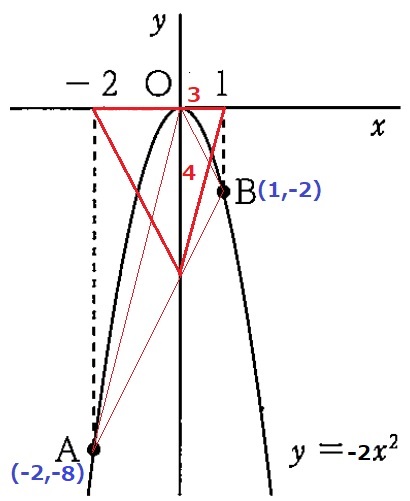
ｙ＝－２ｘ²にそれぞれのｘ座標を代入する。
Ａ（－２、－８）、Ｂ（１、－２）
変化の割合が２⇒傾きが２。
Ｂから左に１、下に２移動して、切片は－２－２＝－４
ｙ＝２ｘ－４

（３）

△ＯＡＢを等積変形すると底辺３、高さ４の三角形になる。
３×４÷２＝６

（４）

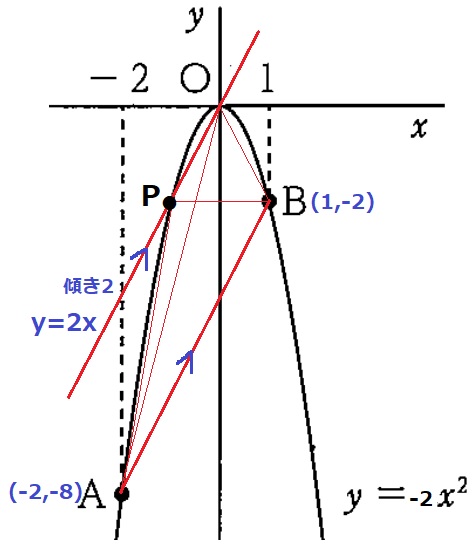
Ｏを通るＡＢに平行な線をひき、ｙ＝－２ｘ²との交点をＰとする。
ＰＯ//ＡＢから等積変形で△ＰＡＢ＝△ＯＡＢになる。
ＡＢの傾きは２なので、ＰＯは原点Ｏを通る傾き２の直線→ｙ＝２ｘ

Ｐはｙ＝－２ｘ²とｙ＝２ｘの交点だから、
－２ｔ²＝２ｔ
２ｔ²＋２ｔ
＝２ｔ（ｔ＋１）＝０
ｔは原点Ｏと異なる、－２≦ｔ≦１なので、ｔ＝－１
Ｐのｙ座標は、ｙ軸について対称であるＢと同じ－２。
P（－１、－２）

＠別解＠
ＯＰの傾きが２、ＯＢの傾きが－２。
ＯＰとＯＢはｙ軸について対称で、ｙ＝－２ｘ²も同様
→これらの交点であるＰとＢもｙ軸について対称→Ｐ（－１、－２）

大問９（平面図形）

（１）
∠ＰＱＤ＝180－110＝70°
ＡＢ//ＣＤの同位角で、∠ＥＰＲ＝70°

（２）
△ＲＥＰ≡△ＲＢＤの証明。

仮定より、ＲＰ＝ＲＤ
前問で∠ＥＰＲ＝70°と出したので、∠ＥＲＰ＝∠ＢＤＲ
対頂角で、∠ＥＲＰ＝∠ＢＲＤ
１辺と両端角が等しいので合同。

（３）
面白い問題です(´ー`)

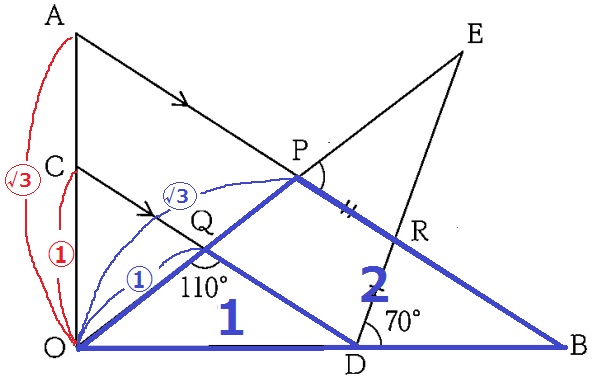
ＡＢ//ＣＤより、ＯＡ：ＯＣ＝ＯＰ：ＯＱ＝√３：１
√３という無理数の比が与えられた⇒２乗して面積比で考えてみよう。
△ＰＯＢ：△ＱＯＤ＝３：１
△ＱＯＤの面積を１とすると、四角形ＰＱＤＢは２。

先ほどの合同で△ＲＢＤを△ＲＥＰに移すと、四角形ＰＱＤＢを△ＥＱＤに変形できる。
△ＱＯＤ：△ＥＱＤ＝ＯＱ：ＱＥ＝１：２

大問10（空間図形）

（１）
△ＯＡＢで三平方→ＯＢ＝２√３ｃｍ

（２）

ア：△ＡＢＣの各辺において、（√７）²＝（√３）²＋２²→ＣＡ²＝ＡＢ²＋ＢＣ²が成り立つ。
　三平方の定理の逆より、△ＡＢＣは∠ＡＢＣ＝90°とする直角三角形。〇
イ：∠ＡＢＣ＝90°より、直径ＡＣとする円の円周上に３点Ａ、Ｂ、Ｃがある。〇
ウ：平行はなく、四角形ＡＢＣＤは台形ではない。
エ：ＡＣを対称の軸として△ＡＢＣと△ＡＤＣは線対称。
　∠ＡＤＣ＝∠ＡＢＣ＝90°で、Ｄは直径ＡＣとする円周上にある。〇
ウ

（３）
四角形ＡＢＣＤ＝△ＡＢＣ×２で計算する。
四角錘ＯーＡＢＣＤの体積は、２×√３÷２×２×３÷３＝２√３ｃｍ^３

（４）

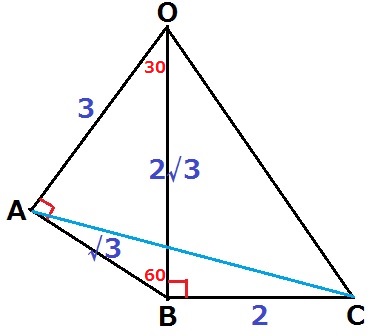
最短距離なので、展開図を作成する。
△ＯＡＢの辺の比に注目すると、√３：２√３：３＝１：２：√３！
内角は30°―60°―90°

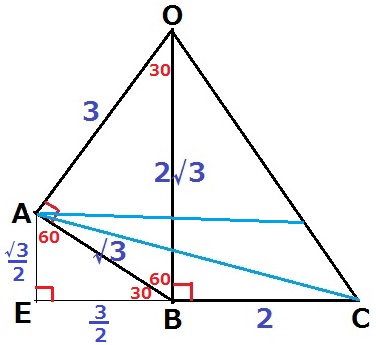
Ａから垂線をひき、ＣＢの延長線との交点をＥとする。
△ＡＥＢも30°―60°―90°で、辺の比は１：２：√３。
ＡＥ＝√３/２ｃｍ、ＥＢ＝３/２ｃｍ
△ＡＥＣで三平方→ＡＣ＝√13ｃｍ

大問11（規則）

（１）

魔方陣の要領で考える。
正五角形は、５×５＝25個

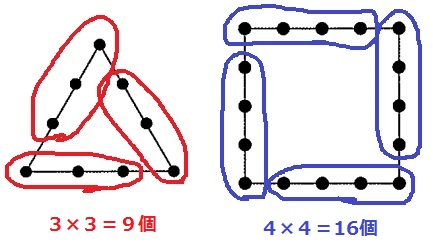
（２）
正ｎ角形は、ｎ×ｎ＝ｎ²個

（３）

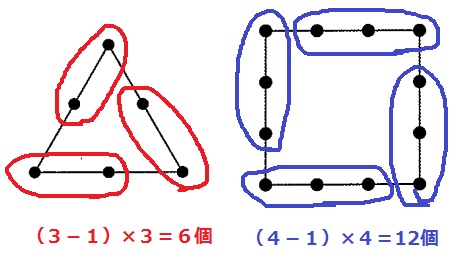
今度は１つの固まりが－１個。
正ｎ角形では（ｎ－１）がｎ個できる。

ｎ（ｎ－１）＝870
ｎ²－ｎ－870　←30×30＝900だから29×30と推測。
＝（ｎ＋29）（ｎ－30）＝０
ｎ＞０より、ｎ＝30
正三十角形