2019年度　沖縄県公立高校入試問題過去問【数学】解説

平均28.9点（前年比；－2.7点）
問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）
４×（－３）＝－12

（２）
４/３－２＝－２/３

（３）
3.8÷４＝0.95

（４）
√２×２√６
＝２√12＝４√３

（５）
（－５ａ）²
＝25ａ²

（６）
２（ｘ＋１）－（１－ｘ）
＝２ｘ＋２－１＋ｘ
＝３ｘ＋１

大問２（小問集合）

（１）
２（３ｘ＋２）＝－８
６ｘ＝－12
ｘ＝－２

（２）
連立方程式。代入法が良いかな？
５ｘ－３ｙ＝９…①
ｙ＝２ｘ－５　…②
②を①に代入。
５ｘ－３（２ｘ－５）＝９
ｘ＝６
ｙ＝２×６－５＝７

（３）
（ｘ＋４）²
＝ｘ²＋８ｘ＋16

（４）
ｘ²－８ｘ＋15
＝（ｘ－３）（ｘ－５）

（５）
③→④で２次方程式を勝手に１次方程式にしている。
ｘ²－３ｘ
＝ｘ（ｘ－３）＝０
ｘ＝０、３
ウ

（６）
√45＝３√５
√５＝2.2360679・・（富士山麓オウム鳴く）
３√５＝３×2.23…＝6.69…≒７

（７）
反比例の一般式：ｙ＝ａ/ｘ
ａ＝ｘｙ＝３×６＝18
ｙ＝18/ｘに代入。
ｙ＝18/２＝９

（８）
対頂角でｘを下にもってくる。
ｘ＝180－（30＋70）＝80°

（９）
数直線で距離が２より大きい数字。
－５/２、３
イ・エ

大問３（データの活用）

（１）
最頻値（モード）は最も表れる数で、ヒストグラムでは突き出ているところ。
突き出ている部分が右側にあれば、平均値が最頻値より小さくなる。
ウ

（２）
ポイントは63点を加味したあとでｘを考える。
31人の中央値は16番目の値。33人の中央値は17番目の値。
31人の16番目の値は60点。
欠席者のうち１人は63点であった。これを加味すると17番目の値は63点となる。
もし、もう１人が60点以下の場合、17番目の値は60点に戻るので、中央値が大きくならない。
よって、中央値を大きくするには61点以上でなくてはならない。

また、31人の平均点が65点で欠席者の１人が63点だから、
もう１人が67点であると平均は変わらない。
（65を真ん中に63は－２、67は＋２なので均すと65）
平均値を小さくするには66点以下である必要がある。
よって、ｘの最小値は61点、最大値は66点。
①…61点、②…66点

大問４（作図）

教科書にある基本レベル。
２点Ａ、Ｂからの距離が等しい→ＡＢの垂直二等分線
これと直線ℓとの交点が点Ｐとなる。

大問５（確率）

（１）
ア：『同様に確からしいとする』ので、どの数も同じ確率で出るものと期待される。○
ｲｳｴ：確率の話では、「必ず」や「つねに」と断定はできない。×
オ：１が出る確率は１/５で、相対度数は１÷５＝0.2
試行回数を多くするほど、大数（たいすう）の法則により0.2に近づいていく。○
ア・オ

（２）①
全体の取り出し方→５×５＝25通り

３で割り切れる数→積ａｂが３の倍数
２回のうち１回は必ず３のカードを出す。
（１、３）（３、１）（２、３）（３、２）（３、３）
（３、４）（４、３）（３、５）（５、３）の９通り。
*式で書けば、５×２－１＝９通り。
３を出して、あとは１～５の５通り。
１回目と２回目の結果を逆にして２倍。
（３、３）は重複するので－１。
したがって、９/25

②
３の倍数＋１で場合分け。
■１→（１、１）
■４→（１、４）（４、１）（２、２）
■７→×
■10→（２、５）（５、２）
■13→×
■16→（４、４）
■19・22→×
■25→（５、５）
計８通りなので、８/25

③
取り出した結果は、３の倍数・３の倍数＋１・３の倍数＋２の３パターンのみ。
①より、３の倍数は９通り。
②より、３の倍数＋１は８通り。
ということは、３の倍数＋２は、25－（９＋８）＝８通り。
よって、３で割り切れる数が最も起こりやすい。ア

大問６（文字式）

（１）
500＋25×80＝2500円

（２）
ｘ＝100のとき、ｙ＝3000＋15×100＝4500
ｘ＝250のとき、250を200と50で分ける。
ｙ＝3000＋15×200＋20×50＝7000
したがって、4500≦ｙ≦7000

（３）
電力会社Ｂは200ｋＷｈが分岐なので、ひとまず200ｋＷｈで試してみる。
Ａ…500＋25×200＝5500円
Ｂ…3000＋15×200＝6000円
Ｂの方が500円高い。

ここから、１ｋＷｈあたりＡは＋25円、Ｂは＋20円かかるので、
５円ずつ差が縮まっていく。
500÷５＝100ｋＷｈ
よって、200＋100＝300ｋＷｈで料金が等しくなる。

大問７（関数）

（１）
Ａの座標をｙ＝ａｘ²に代入。
２＝（－２）²ａ
ａ＝１/２

（２）
ｙ＝１/２ｘ²に、ｘ＝６を放り込む。
ｙ＝１/２×６²＝18

（３）
Ａ（－２、２）→Ｂ（６、18）
右に８、上に16だから、傾きは２。
Ａから右に２いくと、上に４だから、
切片は２＋４＝６
よって、ｙ＝２ｘ＋６

（４）

△ＣＯＰと△ＡＯＢの面積が等しい。
底辺をＢＣで捉えると高さが同じ。
つまり、底辺の長さが同じであれば面積も等しくなる。
→ＡＢ＝ＣＰ
ＡＢのｘ座標は８離れているので、ＣＰのｘ座標も８離れる。
Ｐのｘ座標…－３＋８＝５

前問の式に放り込む。
ｙ＝２×５＋６＝16
Ｐ（５、16）

大問８（平面図形）

（１）
相似の証明。
穴埋めで内容も基本レベル。

対頂角が等しいことから∠ＡＰＢ＝∠ＤＰＣ
もしくは、弧ＡＤに対する円周角から∠ＡＢＰ＝ＤＣＰ
これらから２角が等しいことを示す。
相似であれば辺の比が等しくなり、ＰＡ：ＰＤ＝ＰＢ：ＰＣが導かれる。

（２）①
ＰＡをｘとする。ＰＣ＝２ｘ
ｘ：５＝６：２ｘ
２ｘ²＝30
ｘ²＝15
ｘ＝√15
ＰＡ＝√15ｃｍ

②
面積比は辺の比の２乗。
ＰＡとＰＤが対応する辺。
△ＰＡＢ：△ＰＤＣ
＝√15²：５²＝15：25＝３：５

大問９（空間図形）

（１）
展開図問題。

コツは辺から調べる。
たとえば、辺ＡＢ（赤線）に接する面は２つあり、片方がＣならば他方はＥとなる。

サイコロの組み立てのように、合致する頂点が見えればそれも記入（青い矢印）。
面が横１列のところは両端の辺が重なる（ＢＣ）。
Ａと対極にあるＦがアの位置にくる。

（２）
正八面体は正面からみると正方形になる。
正方形ＡＢＦＤを捉える。

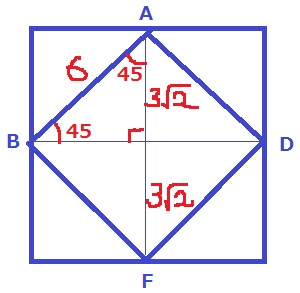
１：１：√２の直角二等辺三角形を見つける。
ＡＦ＝３√２＋３√２＝６√２ｃｍ

（３）
どこで内接するか見極める。

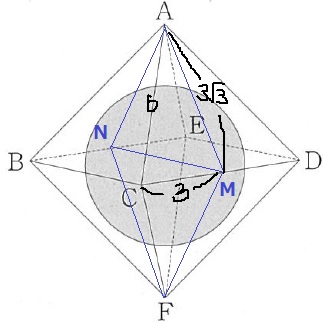
ＣＤ、ＢＥの中点をそれぞれＭ、Ｎとする。
球はＡＭ、ＡＮ上で正八面体に接する。
△ＡＣＭで三平方→ＡＭ＝３√３ｃｍ

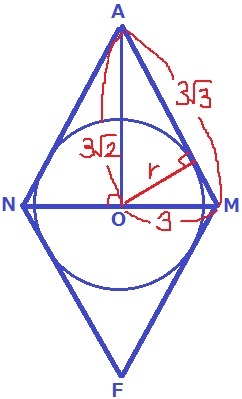
断面図を作成。正八面体の中心をＯとする。
△ＡＭＯで三平方→ＡＯ＝３√２
半径ｒはＡＭに垂直で交わる。△ＡＭＯの面積でｒを計算する。
３√２×３÷２＝３√３×ｒ÷２
ｒ＝３√２×３÷３√３＝√６

球の体積は、４/３πｒ³。
４/３π×√６³＝８√３πｃｍ³

＠余談＠

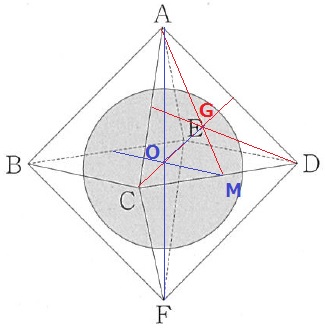
△ＡＣＤの重心で接する。
ＡＧ：ＧＭ＝２：１より、ＧＭ＝√３ｃｍ
ＯＭ＝３ｃｍなので、△ＯＧＭで三平方をするとｒ＝√６ｃｍ
ちなみに、鹿児島でも正八面体が狙われました。大問５です。

大問10（規則）

（１）①
実際にやってみよう。
Ａ→Ｄ→Ｇ→Ｂ→Ｅ→Ｈの順で裏になる。
白はＣ・Ｆ

②
続きを試すと、
Ｈ（６回目）→Ｃ（７回目）→Ｆ（８回目）→Ａ（９回目）
８回目ですべて黒。９回目でＡに帰る。
８回目でオール黒なので、16回目でオール白になる。
16回目

③
初期状態のオール白になるのは16回目。
17回目にＡへ戻り、黒に裏返していく。
16回目までで１ループ。
100÷16＝６…４
初期状態から４回目の状況を調べる。
Ａ・Ｄ・Ｇ・Ｂが黒になる。
よって、白はＣ・Ｅ・Ｆ・Ｈ。

（２）
数が変わっただけで原理は同じ。
試しに裏返してみると、
Ａ→Ｄ→Ｇ→Ｊ→Ｃ→Ｆ→Ｉ→Ｂ→Ｅ→Ｈ（→Ａ）
と、10回目に戻ってくる。
つまり、10回目ですべて黒になり、20回目ですべて白に戻る。
2019÷20＝100…19
19回目の状況を考える。
10回目で黒になり、９回裏返して白にする。
よって、白の数は９個（黒はＨのみ）。

*なぜ、すべてを裏返したあとにちゃんとＡに戻るのか。
２個飛ばしということは３マス進む。
（３と８）（３と10）は互いに素の関係で、１以外に共通の約数を持たないから。
公立高校入試解説ページに戻る