平均53.0点(前年比;+7.9点)
問題はこちら→リセマムさん
大問1(計算)
(1)
-5+2
=-3
(2)
6×(2a+1)/3 ←6と3で約分
=2(2a+1)
=4a+2
(3)
(√7-1)(√7+1)
=(√7)2-12
=6
(4)
y=x+6…①、y=-2x+3…②
x+6=-2x+3
x=-1
①に代入。
y=-1+6=5
x=-1、y=5
(5)
x2-3x-2=0
因数分解ができないので解の公式を適用。
x=(3±√17)/2
大問2(文字式)
式…y=4x、ア
*即答したい。
1辺がxcm。正方形は4辺。
周の長さはy=4xで比例の式。
1次関数はy=ax+b。
大問3(文字式2)
団体X
*解答では理由も記述する。
団体Xの入館料の合計は34a円。
団体Yは割引がきくので、1人あたり20%引き→0.8a円
団体Yの入館料の合計は、0.8a×40=32a円
34a>32aだから、団体Xの方が多くかかる。
大問4(平面図形)
(1)
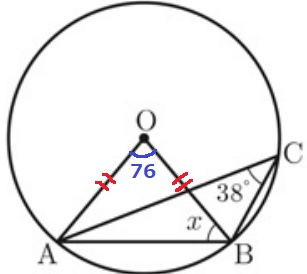
中心角は円周角の2倍→∠AOB=38×2=76°
半径から△AOBは二等辺。
x=(180-76)÷2=52°’
(2)
AB//DC、AD=BCが平行四辺形にならない反例をつくる。
AB//DC、AB=DCならば、1組の対辺が平行でかつ長さが等しいから平行四辺形となるが、
問題文の条件は対辺の関係ではないので平行四辺形の条件を満たさない。
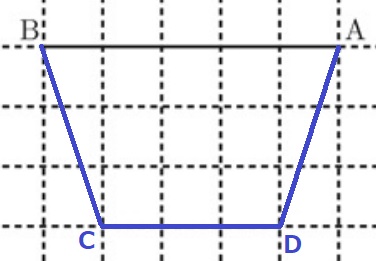
解答は等脚台形を描く。
『四角形ABCD』なのでCが左、Dが右。
長方形は特別な平行四辺形なので×。
大問5(作図)
AがCに重なるような折り目の線分と作図する。
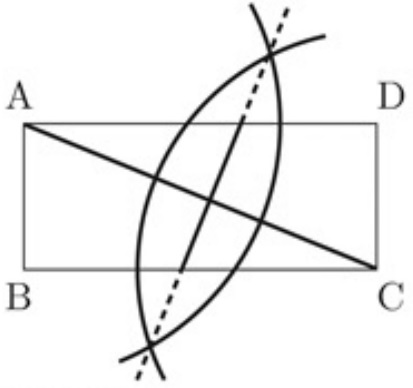
AとCが重なる→AとCは対応する点→線対称
対称の軸はACの垂直二等分線である。
①ACに直線。
②その垂直二等分線。
『折り目の線分』なので、公式解答では折り目でないところは点線で描かれているが、
直線を描いても×にはならないと思う。
大問6(確率)
確率が1/6となる問題を作成する。
2つのサイコロの出目は6×6=36通り
結果が36×1/6=6通りとなるケースを考える。
『同じ目が出る』『和が7である』
もちろん他にもある。
『大の目は3以下で、小の目は5以上』
大問7(比例式)

答案では『用いる文字が何を表すかを示して式をつくり』過程を記述する。
求めたいひろこの当時の身長をxcmとする。
ひろこ:ドア=x:208=3.5:6.5
x=3.5×208/6.5=112cm
大問8(平面図形)
FがCDの中点である証明。

方針は立てやすい。△ADFと△ECFに注目。
仮定からAD=EC
AD//ECから、2つの錯角。
1辺の両端角が等しいので、△ADF≡△ECF
対応する辺は等しい→DF=CF
よって、点Fは辺CDの中点である。
大問9(データの活用)
遠くまで飛ぶであろう飛行機を選び、その理由を述べる。
公式解答をみるとどちらでも良いらしい。
以下、引用。
〔A〕
理由-9m以上の階級の度数の合計が多いから。
〔B〕
理由-最頻値が大きいから。4m未満の階級の度数の合計が少ないから。
*AとBはともに平均が7.0m。
Aはバラつきがあるが、9m以上の度数の合計がBより多い。
また、Bは9m以上飛んだのが1機しかないが、最頻値が6.5mとAの5.5mより長い。
解答は他にも複数あると思われる。
『中央値』を選択した場合、20の中央値(メジアン)は10番目と11番目の平均。
Aの中央値は7.5mだが、Bの中央値は7.0m。(階級値で計算)
バラつきの大きいAに分がある。
ただ、最も起こりやすい飛距離は何かを比較したい場合は最頻値が適している。
中央値は所得格差のような極端な数値がでてくる場合に、その影響を軽減するときに使う。
大問10(数量変化)
(1)
傾きは速さ。
700÷(25-20)=140
(2)
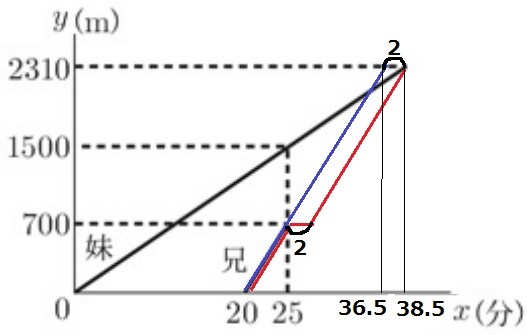
↑青ラインは故障がなかった場合。赤ラインは故障で兄が立ち止まった場合。
速さは変わらないので、傾きは平行。
妹は25分で1500m歩くから、25×2310/1500=38.5分で図書館に着く。
(赤ラインの兄も38.5分で到着)
仮に故障がなければ、兄は2310÷140=16.5分で図書館に着く。
妹の出発から、青ラインの兄は16.5+20=36.5分後に到着。
平行四辺形の対辺は等しいので、差の2を下におろす。
兄が立ち止まっていた時間は2分。
大問11(関数)
(1)
y=1/4x2にx=-4を代入。
y=1/4×(-4)2=4
(2)
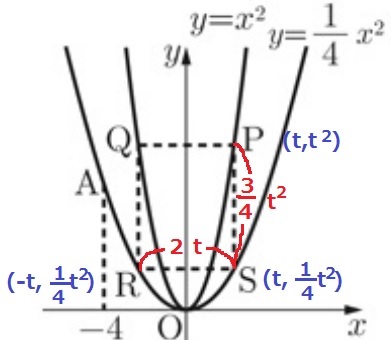
P、Sのx座標をtする。
P(t、t2)S(t、1/4t2)R(-t、1/4t2)
四角形PQRSが正方形→PS=RS
PS=t2-1/4t2=3/4t2
RS=2t
3/4t2=2t
3/4t=2
t=8/3(Pのx座標)
これをy=x2に代入して、y=(8/3)2=64/9
P(8/3、64/9)
大問12(空間図形)
(1)
円柱の体積…3×3×π×6=54πcm2
【球の体積=4/3πr3】
半球の体積…4/3π×33÷2=18πcm3
54π÷18π=3杯分
(2)
ありがたいことに断面図が提供されている。
半径3cmしかわかっていないので、これを断面図に転記したい。

ポイントは『立方体の全ての頂点が球面上にある』
球の半径は中心O~立方体の頂点である。
採用すべき断面図はOのあるAEGC。
AG=6cm

立方体の1辺であるCGを①とする。
△ABCは直角二等辺だから、1:1:√2より。AC=〇√2
△ACGで三平方→AG=〇√3
CG=6×1/√3=2√3
立方体の体積は、(2√3)3=24√3cm3
●講評●
全国で最も大問数が多い岩手。
難問はないので、どこまで素早くかつ正確にこなせるかのタイムアタック形式である。
大問1
死守。ここだけで20点ももらえる。
大問2・3
ほぼ中1の範囲。3は入館料の合計をaであらわして比較する。
大問4
(2)長方形は描かないように!
大問6
確率1/6から6通りとなる事象を考える。見つけやすい。
大問7
昔の写真から当時の身長を計算するというユニ-クな設定であった。
大問8
証明だが基本レベル。
大問9
理由は要点さえあっていれば、文字数は少なくても良い。
大問10
(2)兄が立ち止まることなく図書館に着いた場合を想定する。
大問11
(2)ここもオーソドックスであった。
大問12
球の半径はどこからどこまでの長さか。球と立方体はどこで接しているか。



コメント