2023年度　岩手県公立高校入試問題過去問【数学】解説

平均53.5点（前年比；－4.0点）
０～９点…1.6％、10～19点…6.3％、20～29点…8.2％、30～39点…10.4％、40～49点…14.1％
50～59点…15.2％、60～69点…17.7％、70～79点…15.0％、80～89点…7.9％、90～100点…3.4％
問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）　98％
４－７
＝－３

（２）　71％
２ｘ－（３ｘ－ｙ）
＝２ｘ－３ｘ＋ｙ
＝－ｘ＋ｙ

（３）　72％
（√６＋√２）（√６－√２）
＝（√６）²－（√２）²
＝６－２
＝４

（４）　89％
ｘ²＋10ｘ＋24
＝（ｘ＋４）（ｘ＋６）

（５）　82％
ｘ²－５ｘ＋５＝０
解の公式を適用して、ｘ＝（５±√５）/２

大問２（文字式）

46％
周の長さが４ａの正方形→１辺は４ａ÷４＝ａｃｍ
面積は、ａ×ａ＝ａ²ｃｍ²

大問３（グラフ）

77％
ｙ＝ａｘ→比例。原点を通る直線（ア・ウ）
ｙ＝ａ/ｘ→反比例。双曲線だからイかエ。

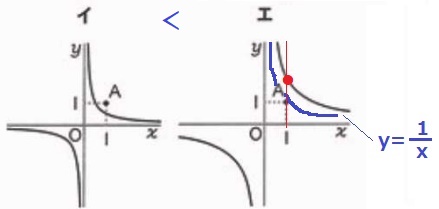
（１、１）を通るとｙ＝１/ｘ（→ａ＝ｘｙ＝１）
これより上にあるエがａ＞１
*ｘ＝１のときｙ＞１→ｘｙ＝ａ＞１
エ

大問４（図形）

（１）　81％

●で線がつながる。直線は扇形の弧の弦。
ウ

（２）　45％

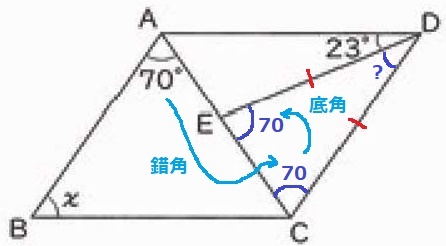
四角形ＡＢＣＤは平行四辺形→ＡＢ//ＤＣの錯角で∠ＤＣＥ＝70°
△ＤＥＣは二等辺三角形。底角は等しいから、∠ＤＥＣ＝70°
∠ＥＤＣ＝180－70×２＝40°
平行四辺形の対角は等しい。∠ＡＢＣ＝∠ＡＤＣ＝23＋40＝63°

（３）　38％

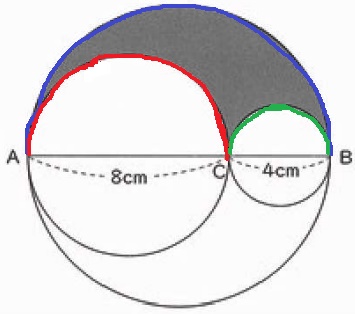
直径４ｃｍ・８ｃｍ・12ｃｍの半円の弧の長さを合計すればいい。
（４π＋８π＋12π）÷２＝12πｃｍ

大問５（作図）

35％

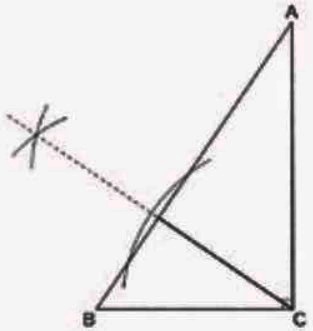
『辺ＡＢを底辺とする高さ』→Ｃを通るＡＢに垂直な線。
垂線の作図をすればいい。

大問６（データの活用）

40％

32人の中央値（Q2）は16番目と17番目の平均。
第１四分位数（Q1）は下位16人の真ん中、下から８番目と９番目の平均。
第３四分位数（Q3）は上位16人の真ん中、上から８番目と９番目の平均。

第３四分位数が15分より大きいので、15分以上は少なくとも８人いる。
答えは「第３四分位数が15分より大きいから」

大問７（確率）

（１）　81％
２人が出すカードの組み合わせは、２×２＝４通り
このうち、Ａが勝つのは【Ａ；チョキ、Ｂ；パー】の１通りしかない。
確率は１/４

（２）　79％
カードの組み合わせは、２×３＝６通り
Ａの勝率が１/２なので、Ａが勝つパターンが６×１/２＝３通りになればいい。

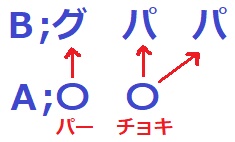
チョキとパー。

大問８（方程式）

72％
答案では用いる文字が何を表すかを示して方程式をつくり、解く過程も書く。
タルト１個をｘ円、クッキー１枚をｙ円とする。
４ｘ＋６ｙ＝1770　…①
７ｘ＋３ｙ＝2085　…②

①÷２をして、２ｘ＋３ｙ＝885　…③
②－①で、５ｘ＝1200
ｘ＝240
③に代入、２×240＋３ｙ＝885
３ｙ＝405
ｙ＝135
タルト…240円、クッキー…135円

大問９（図形の証明）

34％
△ＡＢＣ∽△ＡＤＢの証明。

共通角で、∠ＣＡＢ＝∠ＢＡＤ（★）
半円の弧に対する円周角より、∠ＡＣＢ＝90°
円の接線と半径は直交するから、∠ＡＢＤ＝90°
∠ＡＣＢ＝∠ＡＢＤ
２角が等しいので∽。

大問10（数量変化）

（１）ℓ：28％！、Ｓ：35％

ｘ＝０はＡがＸ線検査機に入った瞬間。
０≦ｘ≦60はＡが中に入る→Ａの横の長さは60ｃｍ、面積は2400ｃｍ²
60≦ｘ≦100はＡ～Ｂ間の40ｃｍ
100≦ｘ≦145はＢが中に入る→Ｂの横の長さは145－100＝45ｃｍ
Ｂの面積Ｓは3750－2400＝1350ｃｍ²
145≦ｘ≦150はＡＢの両方が検査機の中に入っている。
ｘ＝150からＡが出ていく。
検査機の長さℓは、Ａが入り始めてから出始めるまで。すなわち、ℓ＝150ｃｍ
ℓ＝150ｃｍ、Ｓ＝1350ｃｍ²

（２）　７％!!

Ａが入る０≦ｘ≦60の傾きは、2400÷60＝40
150≦ｘ≦210はＡが出るので、傾きは－40である。
（Ａが１ｃｍ左にズレるたびに面積が40ｃｍ²ずつ減る）

傾き－40で（150、3750）の点を通る直線の式を求めればいい。
3750＝－40×150＋ｂ
ｂ＝3750＋6000＝9750
ｙ＝－40ｘ＋9750

大問11（関数）

（１）　58％
ｙ＝ｘ²について、
ｘ＝１のとき、ｙ＝１
ｘ＝２のとき、ｙ＝４
変化の割合＝（ｙの増加量）÷（ｘの増加量）＝（４－１）÷（２－１）＝３

＠別解＠
ｙ＝ａｘ²において、ｘの値がｐ→ｑに増加するときの変化の割合はａ（ｐ＋ｑ）
１×（１＋２）＝３

（２）　９％!!

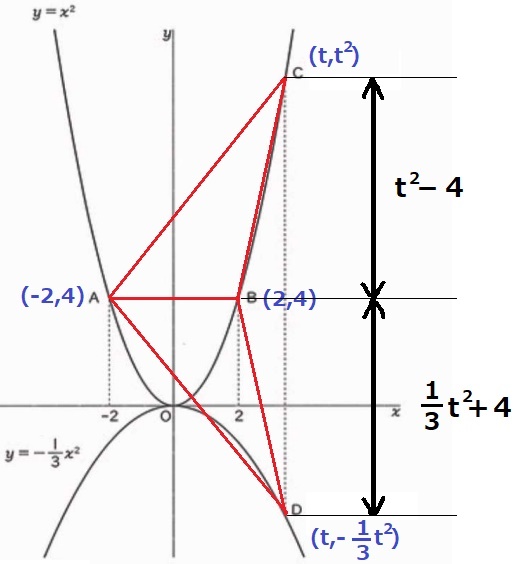
求めるべきＣのｘ座標をｔとする。
Ｃ（ｔ、ｔ²）Ｄ（ｔ、－１/３ｔ²）
△ＡＢＣと△ＡＢＤは底辺ＡＢが共通→高さが等しければ面積も等しい。
△ＡＢＣの高さはｔ²－４、△ＡＢＤの高さは４－（－１/３ｔ²）＝１/３ｔ²＋４

ｔ²－４＝１/３ｔ²＋４
２/３ｔ²＝８
ｔ²＝12
ｔ＞２ゆえ、ｔ＝√12＝２√３

大問12（空間図形）

（１）　63％
△ＡＥＦで三平方→ＡＦ＝√85ｃｍ

（２）　０％!!!

求積すべき四面体を変形する。
ＡＰの中点をＱとする。
上からみると、ＱはＢＤの中点でもあり、面ＤＨＦＢ上にある。
そして、ＡＥとＣＧは面ＤＨＦＢに対して平行。
Ａ→Ｅに移動、三角錐Ａ―ＱＨＦをＥ―ＱＨＦに等積変形。
Ｐ→Ｇに移動、三角錐Ｐ―ＱＨＦをＧ―ＱＨＦに等積変形。
すると、四面体ＡＨＦＰは正四角錘Ｑ―ＥＦＧＨに変わる。

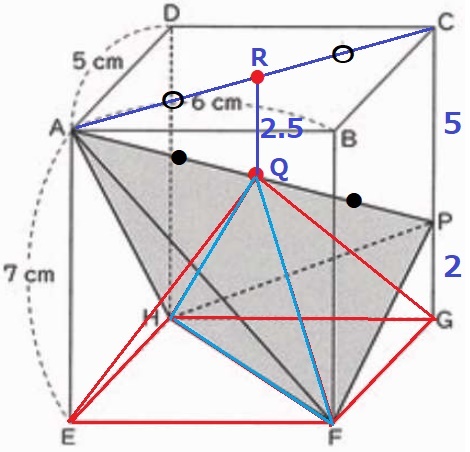
ＣＰ＝７－２＝５ｃｍ
ＡＣの中点をＲとする。
△ＡＱＲ∽△ＡＰＣより、ＲＱ＝５÷２＝2.5ｃｍ

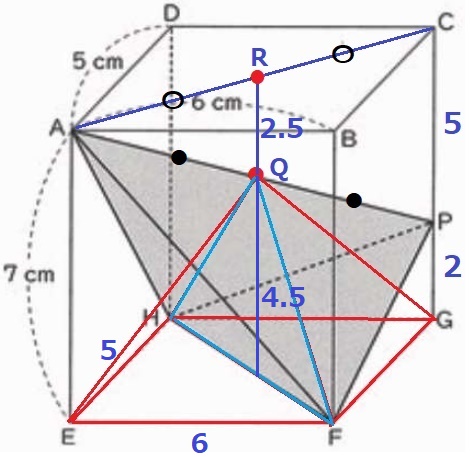
正四角錘の高さは、７－2.5＝4.5ｃｍ
その体積は、５×６×4.5÷３＝45ｃｍ³

平行四辺形の対角は等しいことに気づく。
（３）３つの半円の弧を合わせればいい。
大問５
教科書レベルの作図問題。もっと正解できるはず！
大問６
15分以上の生徒→上位を見る→第３四分位数が15分とどうなのか。
大問７
（２）Ｂのグー、チョキがそれぞれ負けるパターン＝Ａが勝つパターン
大問８
÷２すると、ちょうど和が1200円になった。
大問９
証明問題としては易しい。辺の情報がないので角度で攻める。
共通角＋90°の指摘。
大問10
（１）グラフの意味をつかむこと。
（２）Ｂの面積1350ｃｍ²から（210、1350）と（150、3750）の２点を通る直線でもいいが、
Ａが入る⇒＋、Ａが出る⇒－の変化で、その度合いはＡで同じとわかれば2400÷60で求まる。
大問11
（２）求めたいｘ座標を文字に置き換える形式は公立入試で頻出。
本問は高さだけを抜き出して等式を立てればいい。
大問12
（２）ラス問の正解者は２名だけだったようだ。当たった方、おめでとうございます。
変形の方法を知っていると楽だが、地道にやると計算が大変。
類題が2021年福岡大問６（３）と2022年秋田大問１（15）で出題されている。
公式から発表された階層別での得点率は以下の通り。