2023年度　長野県公立高校入試問題過去問【数学】解説

平均51.5点（前年比；＋4.6点）

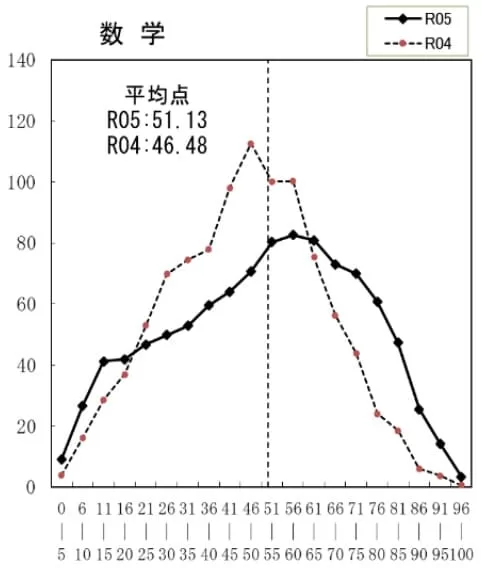
100点―７人、０点―５人
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
－３＋４
＝１

（２）
マイナス×マイナス＝プラス
ｎ＝－６とすると、５－ｎだけ値が正の整数になる。
イ

（３）
（３ｘ－５ｙ）/２－（２ｘ－ｙ）/４
＝｛２（３ｘ－５ｙ）－（２ｘ－ｙ）｝/４
＝（６ｘ－10ｙ－２ｘ＋ｙ）/４
＝（４ｘ－９ｙ）/４

（４）
（ｘ－３）²＋２（ｘ－３）－15　←（ｘ－３）＝Ｘとすると
＝Ｘ²＋２Ｘ－15
＝（Ｘ＋５）（Ｘ－３）　←Ｘ＝（ｘ－３）に直す
＝（ｘ－３＋５）（ｘ－３－３）
＝（ｘ＋２）（ｘ－６）

（５）
ｘ²＋２ｘ－１＝０
解の公式を適用。ｘの係数が偶数なので、ｂ＝２ｂ’が使える。
ｘ＝－１±√２

（６）
ｘとｙの関係を式で表すと、ｙ＝12/ｘ
反比例だからｘの値が２倍、３倍…になると、ｙの値は１/２倍、１/３倍…になる。
ｘとｙの積は比例定数12で一定。
イ・ウ

（７）
30.5の小数第１位を四捨五入すると31ｇ。
31.5を同様に四捨五入すると32ｇ。
30.5を含み、31.5は含まない→30.5≦ａ＜31.5
ウ

（８）
５個の中から１個取り出し、それを戻さずに続けてもう１個取り出す。
→５個から一度に２個取り出す→₅Ｃ₂＝10通り
赤２個から１個、青３個から１個を取り出す組み合わせ→２×３＝６通り
確率は６/10＝３/５

（９）
ｘ＋ｙ＝－１にｘ＝２を代入。
ｙ＝－３
（ｘ、ｙ）＝（２、－３）を代入して成り立つ式を選ぶ。
ｘ－３ｙ＝２－３×（－３）＝11
エ

（10）

Ａを通るＢＣに対して垂直な垂線の作図。

（11）

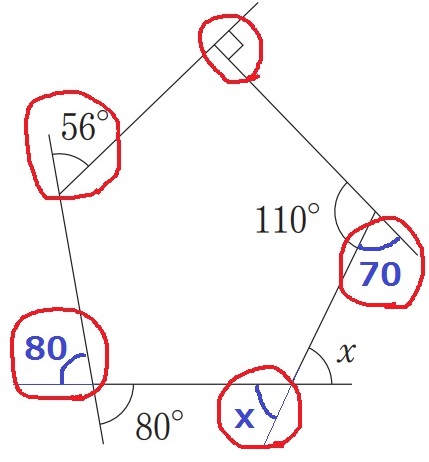
時計回りに外角を統一してみる。
ｎ角形の外角の和は360°だから、
ｘ＝360－（90＋70＋80＋56）＝64°

（12）
【球の体積Ｖ＝４/３πｒ³】
球Ａの体積は、４/３π×３³＝36πｃｍ³
円柱Ｂの高さは、36π÷（２×２×π）＝９ｃｍ

大問２（データの活用＆整数）

Ⅰ（１）
最大値がわかりやすい。
図２の最大値は38～40°の階級に含まれる。
図１で38℃以上は2020年しかない。

（２）①
データの散らばり…範囲＝最大値－最小値
範囲が最も小さいのは2010年、２番目が2020年。
ア

②
2005年の最大値は35℃を超えるので１日はある。
しかし、２日以上あるかもしれない。
ウ
（*31日間の第３四分位数は上から８番目。
これが32℃を超えており、35℃超えが複数日の可能性はある）

（３）
2015年の中央値（第２四分位数；31日間の上から16番目）が30℃超。
全体の50％以上が30℃を超えていた。
一方で、2010年の中央値は34℃超で、全体の50％以上が34℃超。

また、2015年の第１四分位数（下から８番目）が27℃なので、
全体の約25％が27℃以下である。
2010年は最小値が29℃もあり、全体を通してみると2010年の方が暑かった。
あ…イ、い…ア

Ⅱ（１）
ａ＋ｂ＋ｃ＝３ｂの証明。

ａ＝ｍｎ、ｂ＝ｍ（ｎ＋１）、ｃ＝ｍ（ｎ＋２）

ａ＋ｂ＋ｃ
＝ｍｎ＋ｍ（ｎ＋１）＋ｍ（ｎ＋２）
＝３ｍｎ＋３ｍ
＝３ｍ（ｎ＋１）
ｂ＝ｍ（ｎ＋１）だから、３ｍ（ｎ＋１）＝３ｂである。
（*したがって、ａ＋ｂ＋ｃ＝３ｂが成り立つ）

（２）
連続して並ぶ５つの数についても、同様の関係が成り立つという。
仕組み①…（ａ＋ｂ＋ｃ）÷３＝３ｂ÷３＝ｂ
平均の要領で、３つの和を÷３すると真ん中のｂになった。
⇒５つの和を÷５すると真ん中のｃになるはず。
ｃ＝605÷５＝121

仕組み②…ｂ－ｍ＝ｍ（ｎ＋１）－ｍ＝ｍｎ＝ａ
⇒ｃ＝ｍ（ｎ＋２）である点に注意！

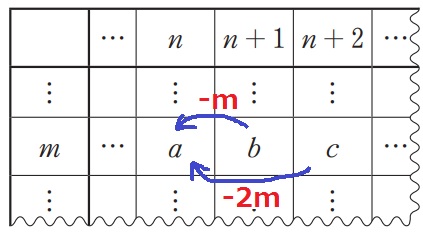
ｃ－ａ＝ｍ（ｎ＋２）－ｍｎ＝２ｍ
ａ＝ｃ－２ｍ＝121－２×11＝99
う…５、え…ｃ、お…99

大問３（数量変化＆関数）

Ⅰ（１）①

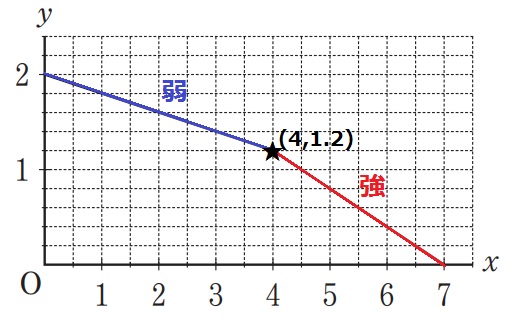
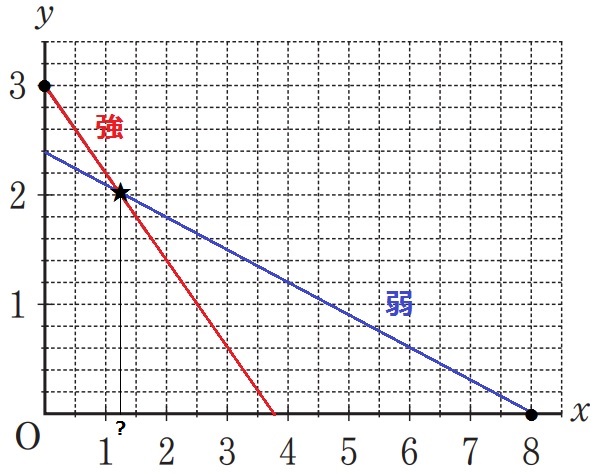
弱⇒強へ切り替えたのは４時間後。
ｙ軸の１目盛りは0.2Ｌ。
右に２目盛り（１時間）、下に１目盛り（0.2Ｌ）の傾きだから、
１時間あたりの放出量は0.2Ｌ。

②
表より、Ａの強運転の傾きは－0.4。
（４、1.2）から左に４移動すると、上に４×0.4＝1.6
切片は1.2＋1.6＝2.8
ｙ＝－0.4ｘ＋2.8

（２）①

最初は水タンクに３Ｌ入れた。
スタートは（０、３）だから、これを通る－0.8の直線（強）をひく。
８時間後に水タンクの水がなくなる。
ゴールは（８、０）だから、これを通る－0.3の直線（弱）をひく。
強から弱に切り替わった時刻は、２直線の交点のｘ座標である。
い…点（８、０）を通り、傾きが－0.3
う…交点、え…ｘ座標

②
強；ｙ＝－0.8ｘ＋３　…①
弱；ｙ＝－0.3ｘ＋ｂ
（ｘ、ｙ）＝（８、０）を代入すると、切片ｂ＝2.4
ｙ＝－0.3ｘ＋2.4　…②

①と②の交点を求める。
－0.8ｘ＋３＝－0.3ｘ＋2.4
0.5ｘ＝0.6
ｘ＝６/５時間後＝１時間12分後

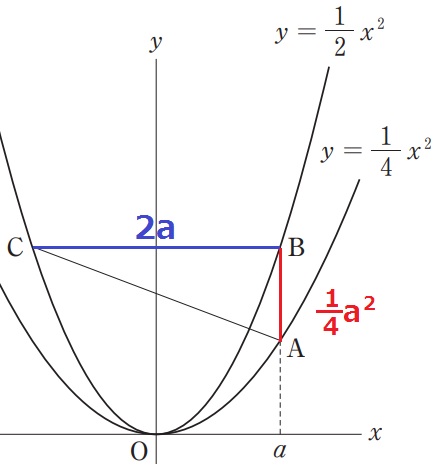
Ⅱ（１）
ＡＢの長さは、Ｂのｙ座標からＡのｙ座標を引く。
ＡＢ＝１/２ｘ²－１/４ｘ²　
＝（１/２－１/４）ｘ²
＝１/４ｘ²
これにｘ＝４を代入して、１/４×４²＝＝４

（２）

ＡＢ＝１/４ａ²、ＢＣ＝２ａの長さが等しい。

１/４ａ²＝２ａ
１/４ａ²－２ａ＝０　←４倍
ａ²－８ａ
＝ａ（ａ－８）＝０
ａ＞０だから、ａ＝８

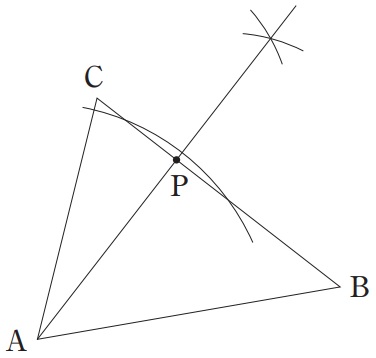
（３）①

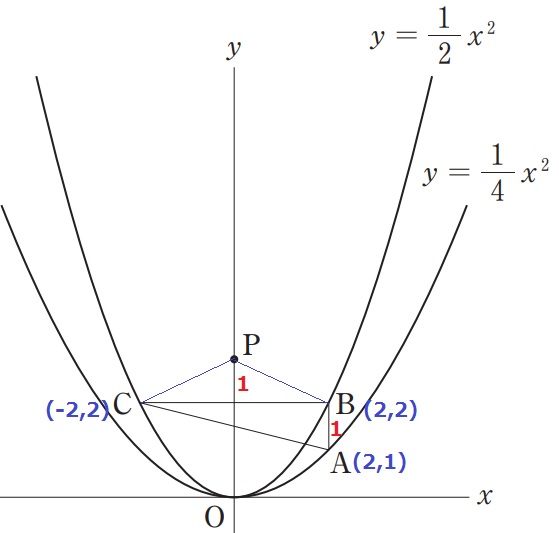
△ＢＣＰ＝△ＡＢＣ→底辺がＢＣで共通→高さが等しい。
ＡＢ＝１だから、ＰとＢＣとの距離も１。
Ｐのｙ座標は２＋１＝３
Ｐ（０、３）

②

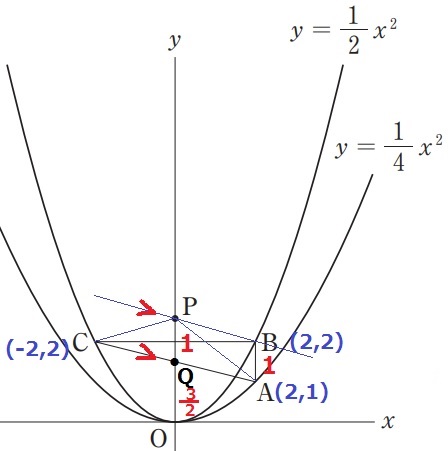
△ＡＣＰ＝△ＡＢＣを等積変形で捉える。
Ｂを通るＡＣに平行な線をひき、ｙ軸との交点がＰである。

ＡＣとｙ軸とのＱとする。
ＡとＣのｘ座標は等しいから、ＱはＡＣの中点→ｙ座標はＡとＣの平均で３/２。
四角形ＡＢＰＱは２組の対辺が平行なので平行四辺形。
対辺は等しく。ＡＢ＝ＱＰ＝１
Ｐのｙ座標は、３/２＋１＝５/２
Ｐ（０、５/２）

大問４（平面図形）

（１）

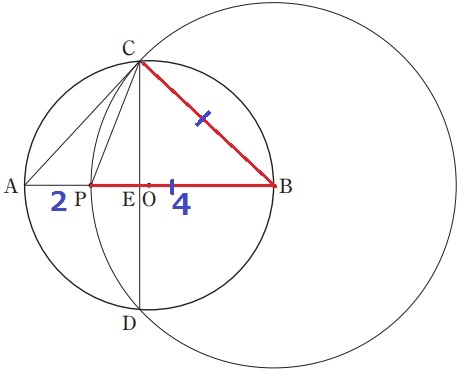
ＢＰ＝６－２＝４ｃｍ
右の大きい円に注目すると、半径よりＢＰ＝ＢＣ＝４ｃｍ

（２）①

∠ＡＣＰ＝●とする。
半径よりＰＡ＝ＰＣ→△ＡＰＣは二等辺だから、∠ＣＡＰ＝●
△ＡＰＣの外角定理で∠ＣＰＢ＝●●

２つの円の半径より、△ＰＢＣは３辺が等しい正三角形。
その内角は等しく、∠ＰＣＢ＝●●
直径ＡＢに対する円周角の∠ＡＣＢ＝●●●＝90°
∠ＡＣＰ＝90÷３＝30°

②
△ＰＥＣの内角は30°―60°―90°だから、辺の比は１：２：√３。
直径ＡＢを対称の軸とすると、ＣとＤは円周上にあってＡＢ⊥ＣＤ。
対称性からＣＥ＝ＤＥ
（すなわち、△ＰＢＣ≡△ＰＢＤ。円の半径から辺の長さがすべて等しい）
ＣＤ＝３×〇２√３/②＝３√３ｃｍ

（３）①
△ＡＢＣ∽△ＣＢＥの証明。

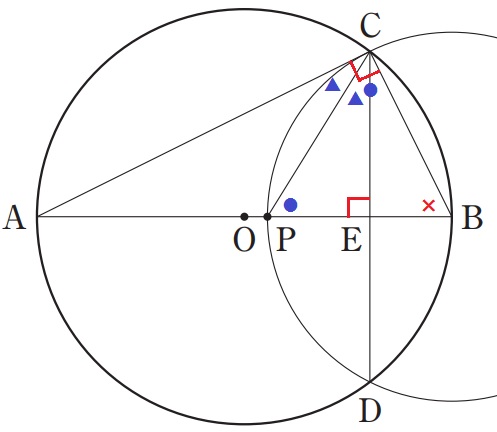
直径に対する円周角から、∠ＡＣＢ＝90°
あ…∠ＡＣＢは円Ｏの半円の弧に対する円周角

②
ＡＢ⊥ＣＤから、∠ＣＥＢ＝90°
∠ＡＣＢ＝∠ＣＥＢまでは問題文に記載済み。

共通角で、∠ＡＢＣ＝∠ＣＢＥ（×）
２角が等しいから∽。

③
ＣＰが∠ＡＣＥを二等分する証明。
∠ＡＣＢ＝90°だから、∠ＡＣＰ＝90－∠ＰＣＢ…①
一方で、ＡＢ⊥ＣＤだから、∠ＣＥＰ＝90°
△ＣＰＥの内角より、∠ＰＣＥ＝90－∠ＣＰＥ…②

半径からＢＣ＝ＢＰ、△ＢＣＰは二等辺三角形である。
∠ＰＣＢ＝∠ＣＰＥ（●）…③
①②③より∠ＡＣＰ＝∠ＰＣＥ（▲）ゆえ、ＣＰは∠ＡＣＥを二等分する。
う…下線部参照、え…ＣＰＥ

（４）①

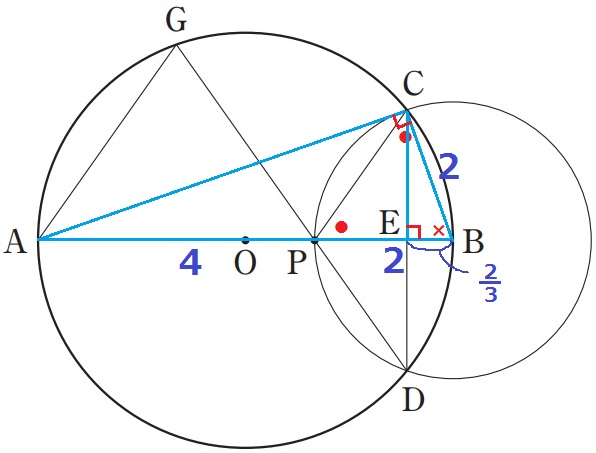
ＢＰ＝６－４＝２ｃｍ
半径ＢＰ＝ＢＣ→△ＢＣＰは二等辺だから、ＢＣ＝２ｃｍ

（３）でＰがＡＢ上のどこにいても△ＡＢＣ∽△ＣＢＥが成り立つとあった。
ＡＢ：ＢＣ＝ＣＢ：ＢＥ＝３：１
ＢＥ＝２×１/３＝２/３ｃｍ

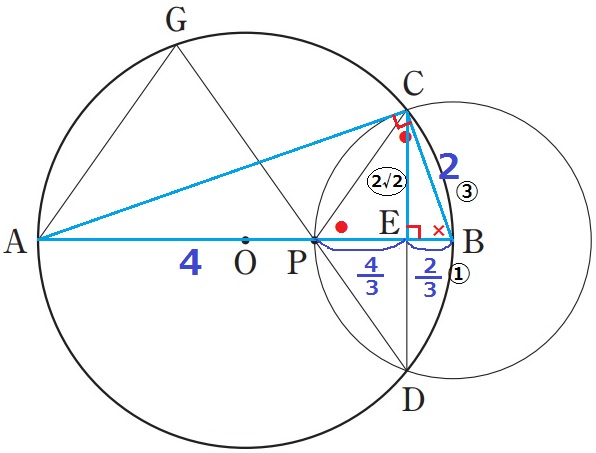
ＰＥ＝２－２/３＝４/３ｃｍ

△ＣＢＥの辺の比に注目する。
ＣＢ：ＢＥ＝③：①だから、三平方の定理でＣＥ＝〇２√２
ＣＥ＝２/３×〇２√２＝４√２/３ｃｍ
△ＣＥＰの面積は、４/３×４√２/３÷２＝８√２/９ｃｍ²

②

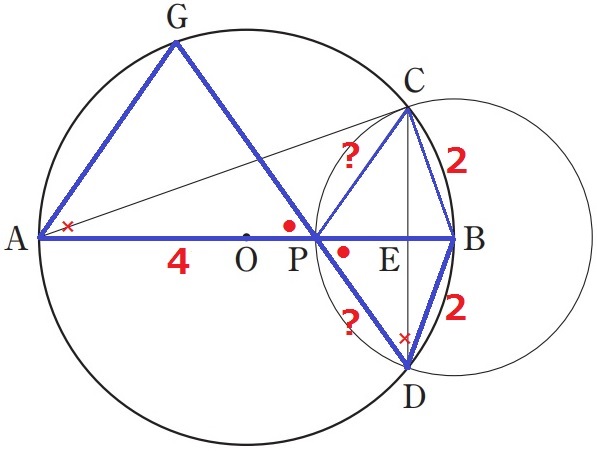
△ＧＡＰはＡＰ＝４ｃｍしか情報がなく、Ｇが離れている場所にある…。
そこで、△ＧＡＰと相似にあたる図形を探す。
（２）②で触れた通り、直径ＡＢを対称の軸とすると、対称性から△ＢＣＰ≡△ＢＤＰ
対頂角と円周角から２角相等で△ＧＡＰ∽△ＢＤＰ
ＡＰに対応するＤＰがわかれば相似比が出せる。

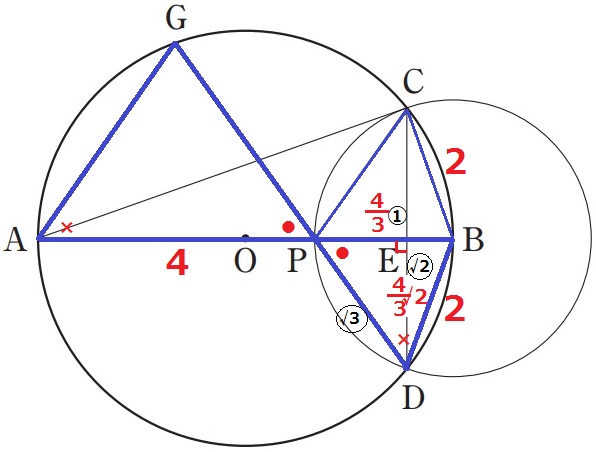
ＤＥ：ＰＥ＝４√２/３：４/３＝〇√２：①
△ＤＰＥの辺の比で三平方→ＣＰ＝〇√３
ＤＰ＝４/３×〇√３＝４√３/３ｃｍ

△ＢＤＰと△ＧＡＰとの相似比は、ＤＰ：ＡＰ＝４√３/３：４＝√３：３
面積比は相似比の２乗だから、△ＢＤＰ（△ＢＣＤ）：△ＧＡＰ＝（√３）²：３²＝１：３