平均27.3点(前年比;-5.7点)

問題PDF
大問1(小問集合)
(1)① 93.5%
-8-5
=-13
② 83.8%
7+3×(-22)
=7+3×(-4)
=7-12
=-5
③ 85.9%
(x-y)/4+(x+2y)/3
={3(x-y)+4(x+2y)}/12
=(3x-3y+4x+8y)/12
=(7x+5y)/12
④ 72.4%
4x2÷6xy×(-9y)
=-6x
⑤ 78.3%
√24-2√3/√2
=2√6-√6
=√6
(2) 72.9%
x2+3x-5=0
解の公式を適用して、x=(-3±√29)/2
(3) 64.1%
x2-8x+12
=(x-2)(x-6) ←x=√7+4を代入
=(√7+2)(√7-2)
=(√7)2-22
=7-4=3
(4) 59.9%
y=x2は下に凸のグラフ。
x=0のとき、最小値y=0
x=3のとき、最大値y=9
0≦y≦9
(5) 48.2%
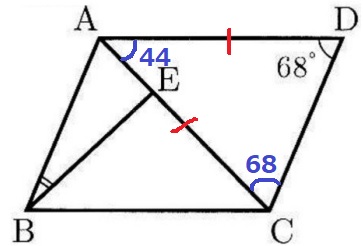
△ACDは二等辺。
∠CAD=180-68×2=44°
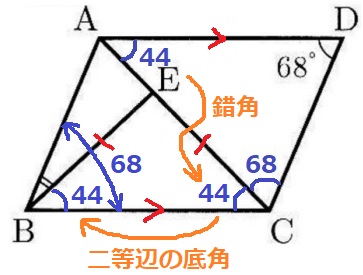
AD//BCの錯角で、∠ACB=44°
二等辺EBCの底角で、∠EBC=44°
平行四辺形の対角は等しいから、∠ABC=68°
∠ABE=68-44=24°
(6)2点…34.7%、1点…8.3%
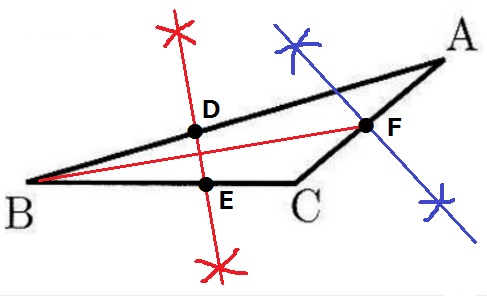
ACの中点をFとする。BがFにくる折り目の両端を作図する。
①ACの垂直二等分線→ACとの交点がF。
②BFの垂直二等分線→これが折り目であり、AB、BCとの交点がD、Eになる。
大問2(関数)
(1) 73.8%
y=x+5にx=1を代入して、A(1、6)
これをy=a/xに代入。
a=1×6=6
(2) 44.7%
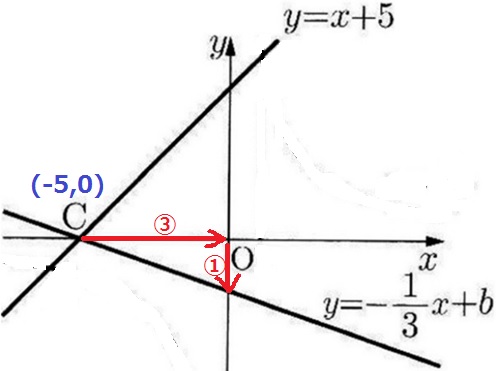
y=x+5にy=0を代入して、C(-5、0)
傾きが-1/3ということは、右に③進むと、下に①さがる。
③=5なので、切片はOから5×①/③=5/3下にある。
b=-5/3
(3) 6.0%!!
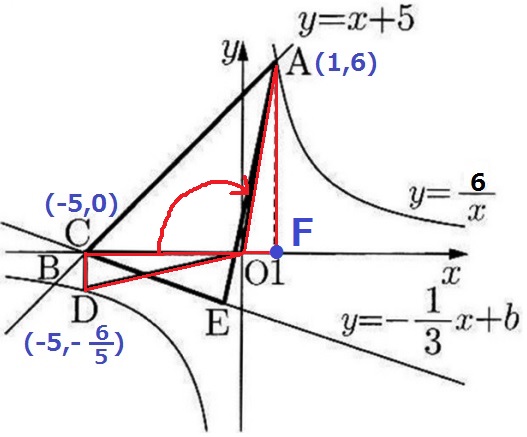
AとDはy=6/x上の点である。
反比例はx座標とy座標の積が等しい→三角形の底辺×高さが等しい=等積
Aから垂線をおろし、x軸との交点をFとすると、△DOCと△AOFは面積が等しい。
(計算すると△DOC…5×6/5=6、△AOF=1×6=6)
△DOCを△AOFに移動させると、四角形ACDOは△ACFに変形できる。
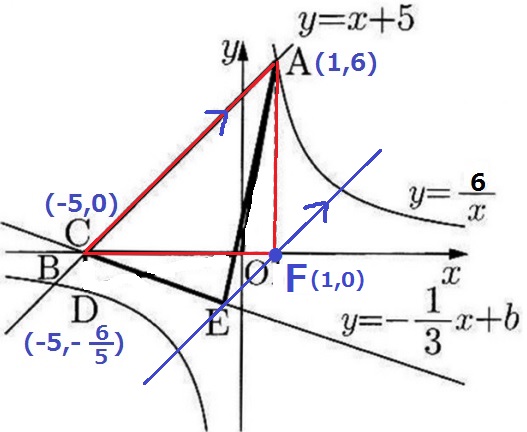
△ACFと△ACEは等積だから、CA//EF
EFの傾きはACと同じで1。EFの切片はFから左に1、下に1移動して-1
EF;y=x-1
BC;y=-1/3x-5/3
これらの交点がEである。
x-1=-1/3x-5/3
x=-1/2
大問3(確率・数量変化)
(1)① 58.9%
6つから2つ選んで花子か太郎を座らせる→順番を考慮するので順列。
6P2=6×5=30通り
② 48.1%
空席2つ以上を調べあげた方が早い。
1に一方を座らせる→他方は4・5・6の3通り
2に座らせる→5・6の2通り
3に座らせる→6の1通り
全部で6通り。逆に座らせる場合を含めると計12通り
確率は12/30=2/5
(2)①2点…24.8%!、1点…13.3%
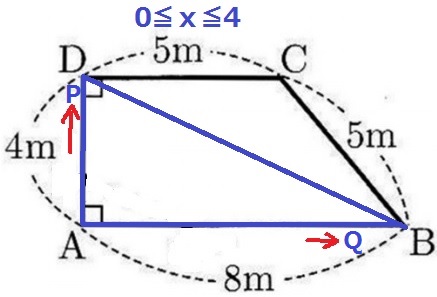
4秒後にPはD、QはBに着く。
0≦x≦4では△AQPの底辺と高さが伸びるので、面積はy=ax2で増加する。
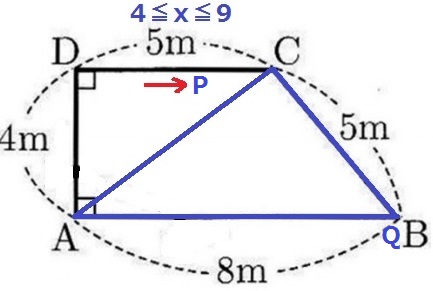
9秒後にPはCに着く。
4≦x≦9では△AQPの面積が変わらない。
14秒後にPはBに着き、△AQPの面積が0になる。
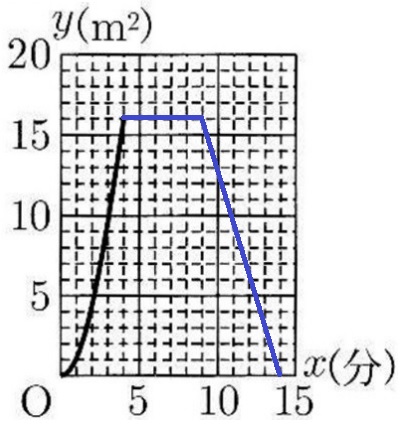
グラフでまとめるとこのようになる。
② 6.4%!!

最初にy=4となるのは、グラフからx=2
計算で求めると、y=ax2に(x、y)=(4、16)を代入して、a=1
y=x2にy=4を代入、x>0からx=2となる。
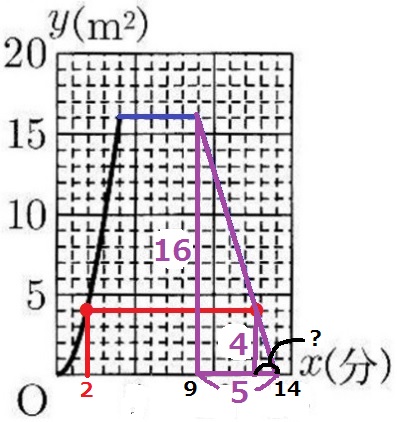
後半は相似を用いる。
?=5×4/16=5/4分=1分15秒
赤線の時間は、14分-(2分+1分15秒)=10分45秒
大問4(方程式)
(1) 64.3%
総和÷個数で平均は求まるが、少しでも時間をかけずに処理したい。

部分的に均してみる。
3.4と3.6の平均は3.5だから、各々の1人ずつを3.5に集める。
同様に、3.9と4.1の5人ずつを4.0に集めると、4.0kmは16人になる。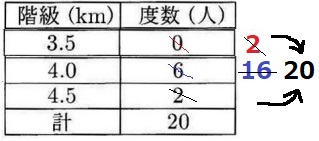
3.5と4.5の2人ずつを4.0に集めると、20人全員を4.0kmに集めることができた。
平均は4.0km
(2)① 15.6%!
通勤距離は(1)の平均値を用いるので、(1)を間違えたら希望はない。
20人全員が車に乗った場合のCO2排出量は、130g×20人×4km
これに削減達成率の36.5%をかければ削減量が出る。
130×20×4×36.5%=3796g
②ア…11.3%!、イ…13.1%!、ウ…13.3%!
路線バスをx人、自家用車をy人とする。
人数で等式。
x+y=20 …①
CO2排出量で等式。
1kmあたり路線バスが57xg、自動車が130ygで、4kmだから4倍する。
全体のCO2排出量は前問の式より130×20×4gで、これに63.5%をかける。
57x×4+130y×4=130×20×4×63.5% ←÷4して×4を削除する
57x+130y=1651 …②
②-①×57をすると、73y=511
y=7
①に代入して、x=13
x=13、y=7
バスに変更した人数は13人
ア…(例)57x×4+130y×4=130×20×4×63.5%、イ…13、ウ…7
@余談@
本問は連立方程式の強制で使えないが、値だけを求めるのであれば方程式を使わない方が楽。
全員車の状態からある人数までバスに切り替えると、①より3796gのCO2が削減できた。
4kmでの結果なので、1kmあたりになおすと3796÷4=949g
1人が車からバスに変えると、1人あたりのCO2削減量は130-57=73g
合計の削減量が949gだから、949÷73=13人が車からバスに切り替えた。
大問5(空間図形)
(1) 67.3%
△ABCで三平方→AC=2√5cm
(2) 26.1%!

AB//FEとなるように、△ABPを奥へ折り返して△FEPと同一平面上にもってくる。
△ABP∽△FEPより、相似比はBP:PE=4:6=②:③
BP=5×②/⑤=2cm
△ABPで三平方→AP=2√5cm
(3)① 2.5%!!
△AFPの特徴をとらえる。

先ほどの△ABP∽△FEPを用いる。
AP:FP=②:③だから、FP=2√5×③/②=3√5cm
△ACFで三平方→FA=3√5cm

△AFPは二等辺三角形。その高さは三平方で2√10cm。
△AFP=2√5×2√10÷2=10√2cm2
② 0.4%!!!

左で底面を△APCとしたときの高さaと、右で底面を△AFPとしたときの高さbを比較する。
ひとまず問題はおいといて、2つの三角錐の底面を△ADPで捉えると、
左の三角錐C―ADPのCをFにスライドすれば右の三角錐F―ADPになる。
つまり、等積変形から2つの三角錐の体積は等しい。
同体積の場合、高さの比は底面積の逆比である。
前問で△AFPの面積が10√2cm2とわかっているので、△ACPの面積がわかればいい。

△BCPで三平方→√40cm
2√5=√20に直してみると、△APCの辺の比は1:1:√2で直角二等辺三角形!
△APC=2√5×2√5÷2=10cm2
高さの比は逆比だから、a:b=△AFP:△APC=10√2:10=√2:1
a/b=√2
大問6(平面図形)
(1)3点…35.1%、2点…3.7%、1点…16.9%、無記入…23.0%
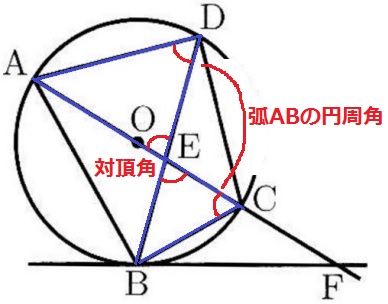
対頂角と弧ABに対する円周角で2角が等しい→∽
(2)① 33.4%
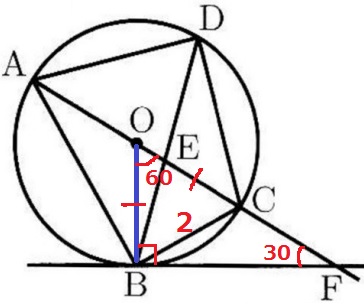
OBに補助線。
半径と接線は直交するから、∠OBF=90°
△OBFの内角で、∠BOF=180-(90+30)=60°
半径より、OB=OC
二等辺三角形OBCの頂角が60°→△OBCは正三角形。
OC=BC=2cm
② 0.1%!!!
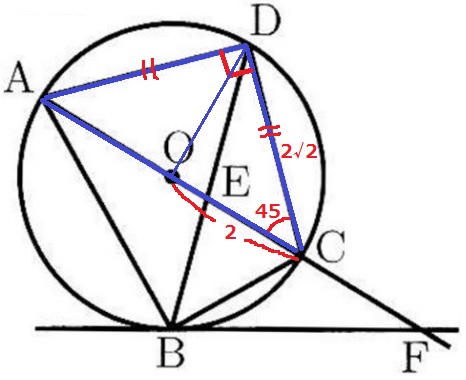
半円の弧に対する円周角は90°だから、∠ADC=90°
DA=DCから△ACDは直角二等辺三角形。
△OCDも同様で、辺の比は1:1:√2なのでCD=2√2cm

弧BCに対する円周角で、∠BDC=60÷2=30°

△CDEをピックアップ。
Eから垂線を引くと、お馴染みの直角三角形が現れる。
左の直角二等辺三角形の等辺を①とおくと、ED=②、CD=〇√3+①である。
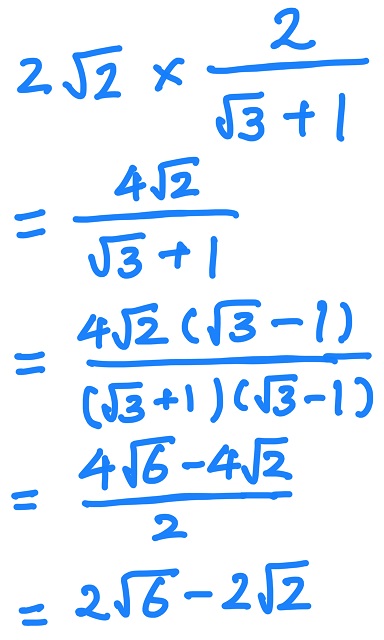
ED=2√6-2√2cm
●講評●
問題の量と質からして高得点は難しい。
大問1
確保しておきたい。
(5)二等辺が2つある。平行四辺形の対角は68°、∠EBCに狙いを定める。
大問2
(2)傾き-1/3はどういう傾きか。
(3)四角形ACDOの変形方法がやや特殊であった。
三角形の頂点が同じ反比例のグラフ上にある場合、三角形の等積を疑う。
大問3
(2)①転換点を調べる。
本問は「4~9秒後は変わらない、9~14秒後は0まで減少する」だけで正解できる。
②全体の14秒から最初と最後の時間を引く。後ろは相似を使うと早い。
大問4
(1)真面目にやると地味に時間がかかる。
真ん中に集めて数を減らしていくやり方は覚えておこう。
(2)①読解力が問われる。数値がきれいではないため処理能力も問われる。
②CO2排出量は36.5%ではなく、63.5%の方である点に注意!
大問5
(2)ここをクリアしないと次も無理。
(3)①△AFPに関する情報を集める。
角度は難しいので辺の長さを求めてみよう。
②2つの三角錐を把握するのが厄介だった…。
高さの比を求めるので底面積と体積の情報が必要。
別の角度から三角錐を眺めると体積が等しい→底面積の逆比を使う。
大問6
(2)①1本の補助線が見えないと沼にはまる。
接点がきたら円の中心と結んでみる。
②見えづらい問題であった。△ACDが直角二等辺であることを察知。
有名角がいろいろでてくるので、どこが使えそうか探す。



コメント