平均44.5点(前年比;-4.6点)
問題はこちら→リセマムさん
2020大阪A問題、2020大阪C問題の解説は別ページ。
大問1(小問集合)
(1) 93.5%
18÷(-6)+(-5)2
=-3+25
=22
(2) 86.9%
(a-1)/2+(a+7)/4
={2(a-1)+(a+7)}/4
=(3a+5)/4
(3) 79.3%
2a2÷ab×(-5b2)
=-10ab
(4) 84.3%
(x+2)2-x(x-3)
=x2+4x+4-x2+3x
=7x+4
(5) 50.3%
ア:-a⇒マイナスがつくので符号チェンジ。
イ:a+2⇒数直線を思い浮かべよう。
a=-2のとき、a+2は0となり、aと同じ負の符号にならない。
(0は正でも負でもない)
-2<a<0の範囲であれば符号チェンジ。
ウ:a2⇒2乗なので常に正になる。aが負であれば符号チェンジ。
エ:a3⇒指数が奇数なので符号が変わらない。〇
オ:1/a⇒aが分母にきただけで符号はaと変わらない。〇
エ・オ
(6) 57.3%
ルートが外れれば自然数になる。
→ルートの中の189nの値が平方数になればいい。
189を素因数分解。
189=3×3×3×7
189n=(3×3)×(21×n)=63×63(←平方数)
最も小さいnは21
(7) 24.5%!
3年生の平均値=3年生の総和÷3年生の人数(8人)
3年生の総和は、全学年の総和から1・2年生の総和を引けばいい。
(3.5×40-3.6×20-4.0×12)÷8
=20÷8=2.5
(8) 78.1%
10a+bは2桁の整数。
2桁の8の倍数を考える。
【16・24・32・40・48・56・64・72…】
サイコロの出目は1~6なので、
【16・24・32・56・64】の5通りだけ。
5/36
(9) 23.0%!
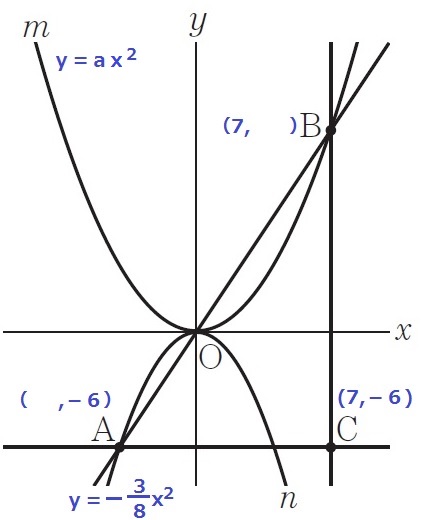
C座標から展開しよう。
Aのy座標が-6なので、これをy=-3/8x2に代入。
-3/8x2=-6
x2=16
Aのx座標は負だからx>0より、x=-4
A(-4、-6)
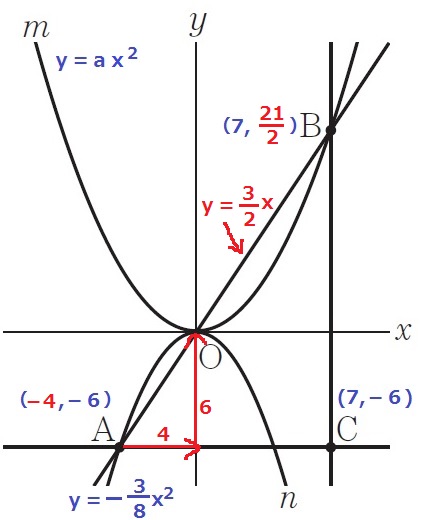
A(-4、-6)→O(0、0)
右に4、上に6なので、AOの傾きは6/4=3/2
AO;y=3/2x
これにBのx座標であるx=7を代入。
y=3/2×7=21/2
B(7、21/2)
これをy=ax2に代入。
21/2=49a
a=3/14
大問2(一次関数)
(1)① ア…97.0%、イ…95.5%
A問題と同じ。体育祭だけを考える。
はじめにタイトルで4秒。写真1枚につき5秒追加される。
ア…4+5×4=24
イ…4+5×7=39
② 88.2%
y=5秒×(写真x枚)+(タイトル4秒)
y=5x+4
③ 88.6%
うえの式にy=84を代入。
5x+4=84
5x=80
x=16
(2) 61.6%
連立方程式。
答案では過程も記述する。
体育祭がs枚、文化祭がt枚。
写真の枚数の合計が50枚なので、
s+t=50…①
体育祭の時間が5s+4秒、文化祭の時間が8t+4秒だから、
(5s+4)+(8t+4)=300…②
①と②の連立方程式を解いて、s=36、t=14
大問3(平面図形)
(1)① 56.3%

△ABEの内角は30°-60°-90°で、1:2:√3の直角三角形。
BE=6×√3/2=3√3cm
② 26.5%!
ODに補助線。
△BDOは半径より二等辺。
∠BOD=180-30×2=120°
半径BOは、6÷2=3cm
弧BDの長さは、3×2×π×120/360=2πcm
(2)① 25.8%!
△ABC∽△BFGの証明。
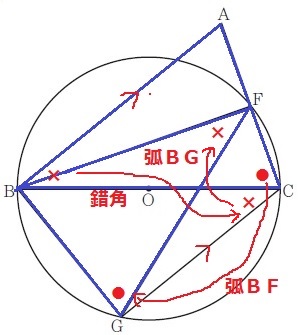
弧BFに対する円周角より、∠ACB=∠BGF(●)
AB//CG→錯角、さらに弧BGに対する円周角につなげて、
∠ABC==∠BCG=∠BFG(×)
2角が等しく∽
②ア 15.3%!
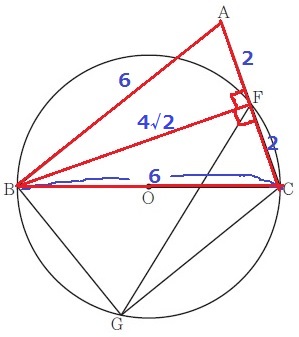
半円の弧に対する円周角は90°なので、∠BFC=90°
△BCFで三平方→BF=4√2cm
△ABCは二等辺三角形。
頂角Bから底辺ACにむけて垂線をおろし、その足がFなので、
FはACの中点にある(斜辺と1鋭角が等しい直角三角形で△ABF≡△CBF)
AF=FC=2cm
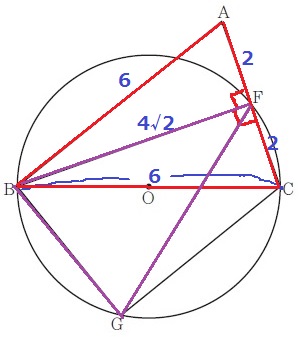
①の二等辺三角形の相似(△ABC∽△BFG)を利用する。
BG:AC=BA:FB=6:4√2
BG=4×4√2/6=8√2/3cm
イ 0.4%!!!
難所です。
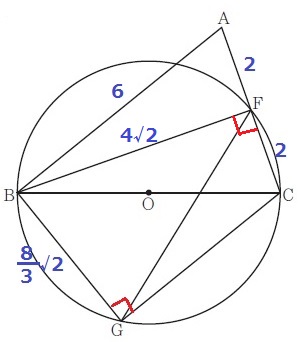
パッと見て直角に目がいくので、
①△BCFと△BCGを合算して四角形BGCFを求める。
②二等辺ABCの面積比から二等辺BFGの面積を求める。
③四角形BGCF-△BFG=△FGC
…となるが、処理手順が多い:;(∩´_`∩);:
そこで、△FGCの形をどうにか変形できないものか。
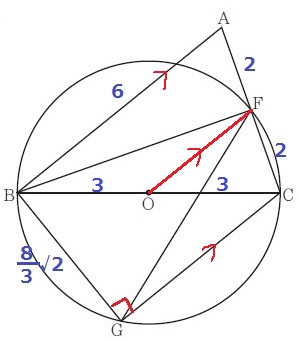
FOに補助線を描いてみた。
FはACの、OはBCの中点なので、
中点連結定理により、AB//FO(//CG)が成り立つ。
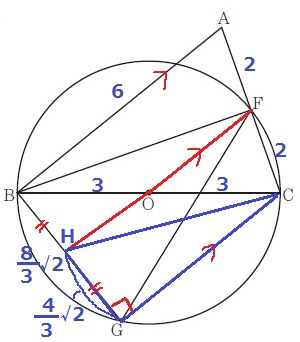
さらにFOを延長して、BGとの交点をHとおく。
AB//FH//CGだから平行線と線分の比より、AF:FC=BH:HG
HはBGの中点にある!
△FGCを等積変形。△HGCを求積すればいい。
HG=8√2/3÷2=4√2/3cm
△BGCで三平方。
GC2=62-(8√2/3)2=36-128/9=196/9
GC>0だから、GC=14/3cm
△HGCの面積は、14/3×4√2/3÷2=28√2/9cm2
大問4(空間図形)
(1)① 93.1%
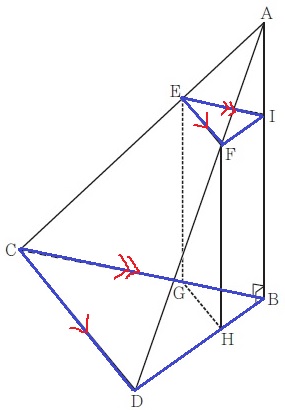
面IEFと面BCDが平行であると見抜ければ、
△IEFの1辺である線分FIと面BCDが平行関係にあるとわかる。
ウ
② 1.2%!!
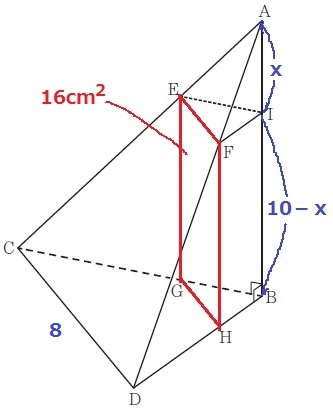
長方形EGHFの面積が16cm2
AB=10cmなので、長方形の縦にあたるFH=10-x
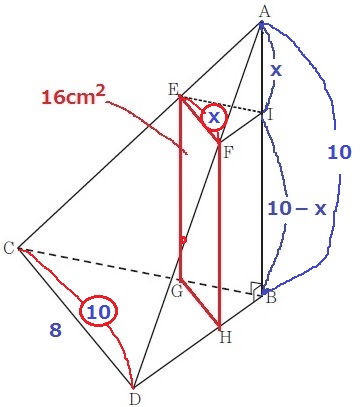
前問で面IEFと面BCDが平行。
三角錐A-IEFと三角錐A-BCDが全体で∽
EF:CD=AI:AB=〇x:⑩
EF=8×〇x/⑩=4/5x
長方形EGHFの横が4/5xcm、縦が10-xcm。
4/5x(10-x)
=8x-4/5x2=16
4/5x2-8x+16=0 ←5倍
4x2-40x+80=0 ←÷4
x2-10x+20=0
解の公式を適用。
xの係数が偶数なので、b=2b’が使える。
x=5±√(25-20)=5±√5
0<x<5だから、x=5-√5cm
(2)① 14.8%!
底辺である△BCDの3辺の長さは判明している。
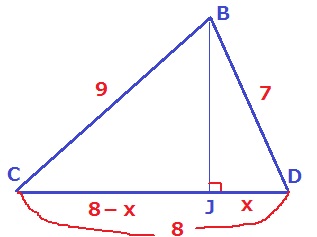
JD=xとすると、CJ=8-x
△BCJと△BDJで三平方。
BC2-CJ2=BJ2=BD2-JD2
92-(8-x)2=72-x2
81-64+16x-x2=49-x2
16x=32
x=2cm
△BDJで三平方→BJ=3√5cm
② 0.6%!!!
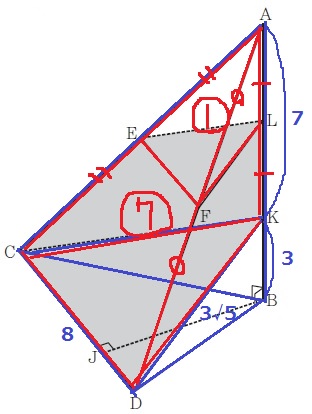
方針【三角錐A-CDK⇒体積比で立体EFL-CDK】
前問のBJから底面の△CDBの面積が求まる。
三角錐A-CDBは底辺△CDB、高さ10cm。
三角錐K-CDBは底辺△CDB、高さ3cm。
三角錐A-CDKは底辺△CDB、高さ7cmの三角錐の体積に等しい。
三角錐A-CDKの体積…8×3√5÷2×7÷3=28√5cm3
問題文の『三角錐A-EFL∽三角錐A-CDK』を使う。
EがACの中点にあることから、相似比は1:2。
体積比は相似比の3乗。
三角錐A-EFLの体積を①とすると、三角錐A-CDKの体積は⑧、
立体EFL-CDKの体積は⑦となる。
28√5×7/8=49√5/2cm3
●講評●
大問1
(5)すべて式だが手早く判定したい。
(6)根号が外れるときのnの値。よくある形式だが正答率は高くはない。
(7)他の平均から3年生の平均を出さないように!
(9)わかる情報をグラフに書き込んで1個ずつ処理する。
大問2
正解率が高い◎
連立ももっと正解できるはず。
大問3
(1)②弧の長さ→半径の長さに集中する。
(2)イここはC問題並みにキツイかった(;∀;)
たまたま平行線を見つけられたが、そうじゃなかったら計算量が倍に増える。
大問4
(1)②長方形の縦と横の長さをxで表す。
解の公式→xの範囲から解を絞るまでコンプリートさせる。
(2)②三角錐の相似は見つけやすいと思う。
あとは時間をどれほど残せたか。



コメント