平均28.2点(50点満点、前年比;+7.2点)

問題はこちら→リセマムさん
大問1(小問集合)
(1) 92.3%
4+6÷(-3)
=4-2
=2
(2) 87.5%
4(2x-y)-(7x-3y)
=8x-4y-7x+3y
=x-y
(3) 85.4%
x2+3x-28
=(x+7)(x-4)
(4) 66.4%
(√2+√7)2
=2+2√14+7
=9+2√14
(5) 72.9%
4x2+7x+1=0
解の公式を適用。
x=(-7±√33)/8
(6) 89.9%
四角錐の展開図を選ぶ→②
①は三角錐、③は三角柱、④は正八面体。
(7) 57.1%
y=3x
比例定数aは3
(8) 74.7%
(大、小)=(6、4)(5、5)(4、6)
3通りしかない。
3/36=1/12
大問2(小問集合2)
(1) 70.6%
標本調査。
標本の数は10ページ。これらの見出し数の平均値を求める。
57+43+58+54+55+58+53+55+67+60 ←順番入れ替え
=(57+43)+(55+55)+(53+67)+60+58+58+54
=100+110+120+60+170=560ページ
10ページの平均は、560÷10=56ページ
母集団は1452ページなので全体の見出し数は、56×1452/10=8131.2
③
(2) 53.2%
三平方の定理。
( )2+( )2=73が成立すればいい。
正方形の辺の長さから、平方数を取り出してみる。
32=9
52=25
22=4(DE)
82=64(BF)
9+64=73
△ABFのAFが√73cmとなる。
線分AF
(3) 39.8%(部分正答22.8%、無答16.7%)
連立方程式。
解答では求める過程も記述する。
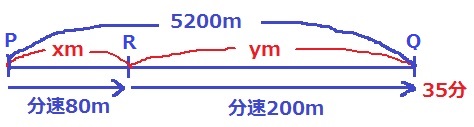
混乱したときは、図を描いて情報を整理しよう。
歩いた距離(PR間)をx、走った距離(RQ間)をyとする。
距離で等式;x+y=5200 …①
時間で等式:x/80+y/200=35 …②
②を400倍して分母を払うと、5x+2y=14000 …③
③-①×2をして、3x=3600
x=1200
①に代入、y=5200-1200=4000
P地点からR地点は1200m、R地点からQ地点は4000m
大問3(データの活用)
(1) 62.7%
最頻値(モード)…最もあらわれている値。
【まとめⅠ】の度数分布表の休日で、最も度数(日)が大きいのは80~100(分)の38日。
解答は階級値で答える。80と100の平均で90。
(2) 30.1%!
相対度数は小数で求める。
小数第何位まで書くべきか指定がない。
表の相対度数が小数第2位なので、小数第3位を四捨五入して小数第2位まで求める。
ア:9÷31=0.290…→0.29
イ:31÷185=0.167…→0.17
ウ:待ち時間が40分未満の相対度数が大きい①日曜日の方が、待ち時間が短くなりそう。①
大問4(整数)
(1) 46.7%(部分正答19.0%)
整数の証明問題。
『大きい方から1番目の数と2番目の数の積と、小さい方から1番目と2番目の数の積の差』
(n+3)(n+2)-n(n+1)
=n2+5n+6-n2-n
=4n+6
『連続する4つの整数の和』
n+(n+1)+(n+2)+(n+3)
=4n+6
*仮定と結論の部分は解答用紙に書かれている。
空欄には2つの事柄を並べ、どちらも計算結果が4n+6であることを示せばいい。
@余談@
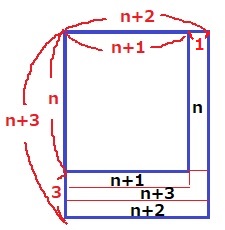
↑幾何でいうとこんな感じ。
1辺がn+2、n+3の大きな長方形から、1辺がn+1、nの小さい長方形を引くと、
L字の部分が差にあたる。これを4分割するとn、n+1、n+2、n+3の和になる。
(2) 30.7%!(無答25.1%)
2つの異なる問題から、共通する性質を見つける。
前問と同様、立式して計算する。
【性質Ⅰ】
連続する4つの整数をm、m+1、m+2、m+3とする。
(m+1)(m+3)-m(m+2)
=m2+4m+3-m2-2m
=2m+3
【性質Ⅱ】
連続する5つの整数をn、n+1、n+2、n+3、n+4とする。
(n+1)(n+4)-n(n+3)
=n2+5n+4-n2-3n
=2n+4
この2つが何の和なのかを考える。
和なので、(文字+〇)+(文字+〇)の形を想像する。
連続する整数の数が1つ違いで、両者の差が1である点もヒントになる。
性質Ⅰでは、2m+3=m+(m+3)
性質Ⅱでは、2n+4=n+(n+4)
つまり、最も大きい数と最も小さい数の和。
大問5(平面図形)
14.2%!(部分正答47.0%、無答15.7%)
△COE≡△ODFの証明。
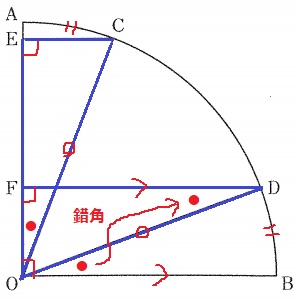
∠CEO=∠OFD=90°
半径から、CO=OD
等しい弧に対する円周角は等しいので、∠AOC=∠BOD=●
∠AFD=∠AOB=90°より同位角が等しい→FD//OB
錯角で∠BOD=∠ODF=●
(整理すると、∠COE=∠ODF=●)
以上、斜辺と他の1鋭角が等しい直角三角形ゆえに合同。
大問6(関数)
(1) 55.2%
底辺OEが5、高さはAのy座標4。
5×4÷2=10
(2) 4.4%!!
独特なやりにくさを感じる。
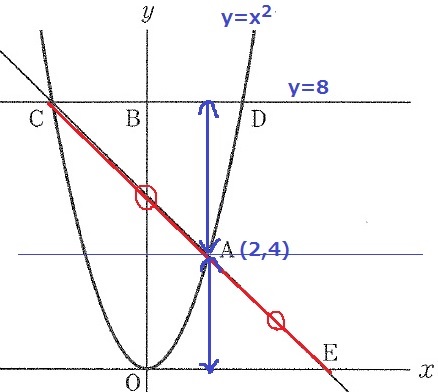
Aを通るx軸に垂直な線分をひき、上下の三角形をみると、
CA=AE、直角、対頂角(または錯角)から斜辺と1鋭角が等しい直角三角形なので合同。
2つの三角形の高さは等しく、ここからB・C・Dのy座標が8であるとわかる。
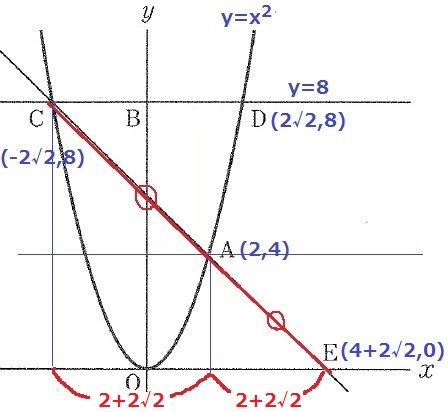
y=x2にy=8を代入。
x=±2√2
C(-2√2、8)
D(2√2、8)
CとAから垂線をひくと相似関係にある三角形があらわれる。
CとAのx座標の差が2+2√2。
AとEのx座標の差も2+2√2で、E(4+2√2、0)
求めたいのはDEの傾き。
傾き=(yの増加量)/(xの増加量)
(0-8)/(4+2√2-2√2)=-8/4=-2
易化。以下、公式の検査結果を参照。
『60%を越える得点層に属する受検者が大幅に増加した。
一方、30%以下の得点層に属する受検者は大幅に減少したものの、全体の18.8%と少なくない』
難関校を狙うには8割はとっておきたい。
大問1
全体的に得点率が高い。(7)比例定数は中1で習うが、正答率が6割弱だった。
大問2
(1)もっと出来が悪いと思いきや、7割以上が正解していた。
(2)辺の組み合わせは少ないが、変化球のある設問だったからか正答率は約半数。
大問3
問題文が長い割に設問は大したことなかった。
(2)小数第〇位の指定がないと不安になる。
大問4
(1)も(2)も基本は立式→計算の流れ。
(2)は最後に共通の性質を見つけ出す作業があった。
大問5
部分正答を含めると6割超。完全正答を狙おう。
大問6
(1)平易過ぎる設問だが正答率が55%。
最初の小問は難しくないという認識でチャレンジしよう。
(2)本試験の難所。初手はCBDのy座標を確定する。
シンプルなグラフから補助線をひき、合同や相似の図形を見出す。




コメント