2020年度　大阪府立高校入試Ｃ問題過去問【数学】解説

平均41.3点（前年比；－16.7点）
問題はコチラ→ＰＤＦファイル
Ａ問題、Ｂ問題の解説はコチラ。

大問１（小問集合）

（１）　96.5％
３/８ａ²ｂ÷９/４ａｂ²×（－３ｂ）²
＝３/８ａ²ｂ×４/９ａｂ²×９ｂ²
＝３/２ａｂ

（２）　87.1％
（６－√18）/√２＋√２（１＋√３）（１－√３）
＝（６√２－６）/２＋√２｛１²－（√３）²｝
＝３√２－３－２√２
＝√２－３

（３）　81.2％
（ｘ－１）²－７（ｘ－１）－８＝０
（ｘ－１）をＸに置き換え。
Ｘ²－７Ｘ－８
＝（Ｘ＋１）（Ｘ－８）　←Ｘをｘ－１に戻す
＝（ｘ－１＋１）（ｘ－１－８）
＝ｘ（ｘ－９）＝０
ｘ＝０、９

（４）　54.1％
ｘ＝３のとき、ｙ＝ａ/３
ｘ＝５のとき、ｙ＝ａ/５
【変化の割合＝ｙの増加量/ｘの増加量】

ａ＝－15

（５）　72.9％
条件整理。

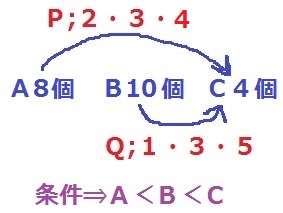
Ａ８個、Ｂ10個、Ｃ４個。
Ｐ；Ａ→Ｃに２個or３個or５個移動。
Ｑ；Ｂ→Ｃに１個or３個or５個移動。
移動後の個数がＡ＜Ｂ＜Ｃとなる確率を求める。

◆Ａ＜Ｂ
Ａが８個、Ｂが10個。差はＢ－Ａ＝２
ＱがＰより２以上大きいと、Ａ≧Ｂとなり不適。
（Ｐ、Ｑ）＝（２、１）（２、３）（３、１）（３、３）（４、１）（４、３）（４、５）

◆Ｂ＜Ｃ
うえの７通りのうち、ＣがＢより多くなるパターンを絞る。
たとえば、（Ｐ、Ｑ）＝（２、１）ならば、Ｃは４＋２＋１＝７個となり、
Ｂは10－１＝９個でＢ＞Ｃとなるから不適。
（Ｐ、Ｑ）＝（２、３）（３、３）（４、３）（４、５）
以上４通り。
したがって、４/９

（６）　38.8％
算数で解きます。

↑８年分はあらかじめ均して長方形に整理。
長方形の上の辺が８年の平均値。

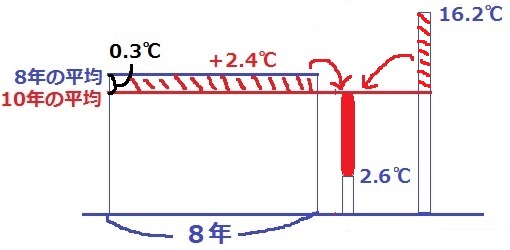
2.6℃と16.2℃を加えて、10年で均すと平均値は0.3℃下がる。
10年の平均値より上にある長方形の上部0.3×８＝2.4℃と、
16.2℃の上部が2.4℃を埋めることで10年の平均値になる。
→長方形の上部2.4℃を右の２年に合算し、右の２年を均すと10年の平均値となる。
2.4＋2.6＋16.2＝21.2℃
21.2÷２＝10.6℃

＠別解＠
算数大好きさん（@kimagure_mana）より素敵な解法を頂きました。

求めたい10年の平均値を支点に設定。
両サイドは２年の平均9.4℃、８年の平均□＋0.3℃で、
支点からの距離は２：８＝１：４の逆比。
①＝0.3℃から計算すると10.6℃となります。
*天秤法は食塩水の濃度問題でメジャーですが、平均でも応用できるのですね！
多少の慣れが求められますが、こういう問題は算数の方が処理が少ないのでオススメです。

（７）　21.8％！
シンプルだが厳しい。
こういう整数論は文字を使って等式を立ててみる。
93の倍数⇒93ｋ、素数⇒ｐ
　2020－ｎ＝93ｋ…①
＋)ｎ－780＝　ｐ…②
1240＝93ｋ＋ｐ

93をｋ倍して素数ｐを足すと2020になる。
試しに2020を93で割ってみる。
2020÷93＝13…31
ちょうど余りの31が素数であり、ｋ＝13、ｐ＝31と出てしまう(;’∀’)
これを②に代入して、ｎ－780＝31
ｎ＝811
*運良く出てしまったが・・1240と93を観察するといずれも31の倍数なので、
1240＝93ｋ＋ｐ
ｐ＝1240－93ｋ＝31（40－3ｋ）
31が素数なので、31（40－３ｋ）を素数のままにするには、
40－３ｋが１のときしかない。（31×１＝31）
40－３ｋ＝１
ｋ＝13
①に代入して、ｎ＝811となる。

（８）　48.7％
答案では過程も記述する。

Ａ（４、16ａ）
Ｂ（－２、－２ｂ＋４）
ＡとＢのｙ座標を手がかりに、16ａ＝－２ｂ＋４…①

ℓ//ｎからｎの傾きはｂ、切片は３だから、ｎ；ｙ＝ｂｘ－３
Ｄ（４、４ｂ－３）
正方形ＡＢＣＤの１辺はＡとＢのｘ座標の差である６ｃｍ。
ＡＤ＝16ａ－（４ｂ－３）＝６
16ａ－４ｂ＝３…②

①と②で連立。代入法が使える。
②の16ａに①の－２ｂ＋４を代入。
－２ｂ＋４－４ｂ＝３
ｂ＝１/６
①に代入。
16ａ＝－２×１/６＋４
ａ＝11/48
ａ＝11/48、ｂ＝１/６

大問２（平面図形）

（１）　30.1％！
四角形ＥＡＣＦが平行四辺形である証明。

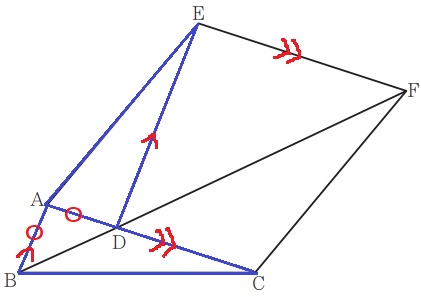
ＡＣ//ＥＦと１組の対辺の平行がわかっているので、
２組の対辺が平行であるか（ＡＥ//ＣＦ）、
１組の対辺が平行でかつ長さが等しいか（ＡＣ＝ＥＦ）。
ＡＥ//ＣＦは錯角や同位角を見つけにくいので、
合同図形や平行線を頼りにＡＣ＝ＥＦの導出に的を絞る。

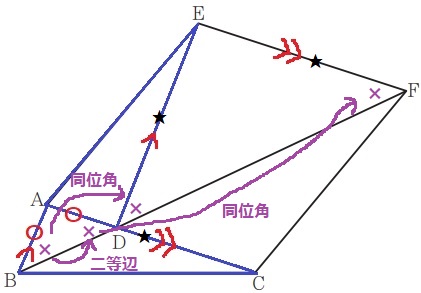
二等辺ＡＢＤの底角→∠ＡＢＤ＝∠ＡＤＢ（×）
ＡＢ//ＥＤの同位角→∠ＡＢＤ＝∠ＥＤＦ（×）
ＡＣ//ＥＦの同位角→∠ＡＤＢ＝∠ＥＦＤ（×）
△ＤＥＦにおいて２つの底角が等しい→二等辺三角形
ＥＦ＝ＥＤ（★）
△ＤＡＥ≡△ＡＢＣより、ＥＤ＝ＣＡ（対応する辺に気を付けよう！）
以上より、ＥＦ＝ＣＡが導かれ、１組の対辺が平行かつ長さが等しく、
四角形ＥＡＣＦは平行四辺形となる。

（２）①　83.5％

△ＡＣＧで三平方→ＣＧ＝４√２ｃｍ
△ＢＣＧで三平方→ＢＣ＝４√３ｃｍ

②　20.0％！

ＣＧとＤＥの交点をＩとする。
ＥＨを１辺とする三角形は△ＥＨＩ。
ＢＧ//ＤＥにより、△ＥＨＩ∽△ＡＨＧ
ＡＥ＝ＢＣ＝４√３ｃｍであるから、ＡＨ：ＥＨさえわかればいい。
ＡＨ：ＥＨ＝ＡＧ：ＥＩ
前問の証明の通り、ＤＥ＝ＡＣ＝６ｃｍなので、ＥＩの長さを知りたい。

ＡＧ//ＤＩより、△ＡＣＧ∽ＤＣＩ
△ＡＢＤは二等辺なので、ＡＤ＝２ｃｍ、ＤＣ＝４ｃｍ
ＤＩ＝２×４/６＝４/３ｃｍ
ＩＥ＝６－４/３＝14/３ｃｍ
ＡＨ：ＥＨ＝ＡＧ：ＥＩ＝２：14/３＝３：７
ＥＨ＝４√３×７/10＝14√３/５ｃｍ

③　8.2％!!

四角形ＥＨＣＦ＝平行四辺形ＥＡＣＦ－△ＡＣＨ
前問でＡＨ：ＨＥ＝３：７をわかったので、
△ＡＣＨの面積を【３】とすると、△ＨＣＥの面積は【７】
ＣＥは平行四辺形の対角線で、△ＣＥＦの面積は△ＣＥＡと同じ【10】
つまり、平行四辺形ＥＡＣＦの面積の17/20倍をすれば四角形ＥＨＣＦとなる。
平行四辺形ＥＡＣＦの面積が知りたい。

高さは直角のあるところに目をつける。
∠ＢＧＣ＝90°
△ＡＢＣ＝２×４√２÷２＝４√２ｃｍ²
合同より、△ＡＤＥ＝４√２ｃｍ²
ＡＤ：ＤＣ＝２：４＝１：２だから、
△ＡＤＥの面積を①とすると△ＤＣＥは②、△ＣＥＦは③。
平行四辺形ＥＡＣＦの面積は⑥となる→４√２×６/１＝24√２ｃｍ²
したがって、四角形ＥＨＣＦの面積は24√２×17/20＝102√２/５ｃｍ²

大問３（空間図形）

（１）①　58.8％
ＥＪ＋ＪＩが最小→直線
展開図を作成。

問題文にあるように、四角形ＥＡＤＨとＨＧＣＤは長方形。
△ＥＪＨ∽ＩＪＤより、ＨＪ：ＪＤ＝ＥＨ：ＩＤ＝４：３
ＨＪ＝８×４/７＝32/７ｃｍ
△ＥＪＨの面積は、４×32/７÷２＝64/７ｃｍ²

②　31.8％！
角度が同一平面上にない。
そういうときは、同じ面に写してみよう。

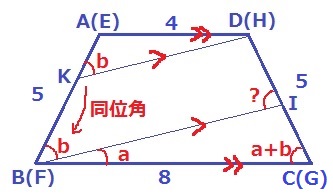
奥の四角形ＥＦＧＨを手前の四角形ＡＢＣＤに投影。
ＫＤ//ＢＩより、同位角で∠ＡＢＩ＝ｂ
四角形ＡＢＣＤは等脚台形なので、∠ＡＢＣ＝∠ＤＣＢ＝ａ＋ｂ
△ＢＣＩで外角定理→∠ＢＩＤ＝ａ＋（ａ＋ｂ）＝２ａ＋ｂ

③　9.4％!!
四角形ＥＦＧＨだけだと情報が足りないので、先ほどの投影した図を用いる。

ＤＫとＣＦ（ＣＢ）を延長、交点をＬとする。
△ＦＣＩ∽ＬＣＤより、ＬＣ＝８×５/２＝20ｃｍ
ＬＦ＝20－８＝12ｃｍ
△ＡＫＤ∽△ＦＫＬより、ＡＫ：ＫＦ＝ＡＤ：ＦＬ＝４：12＝１：３
ＫＦ＝５×３/４＝15/４ｃｍ

（２）①　39.2％

ＤＦを対角線とする直方体をみつける。
辺の長さがａ、ｂ、ｃの直方体の対角線→√（ａ²＋ｂ²＋ｃ²）

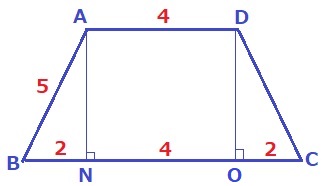
直方体の高さを求める。
ＡとＤから垂線、足をＮ、Ｏとする。
等脚台形は左右対称。ＢＮ＝（８－４）÷２＝２ｃｍ
△ＡＢＮで三平方→ＡＮ＝√21ｃｍ

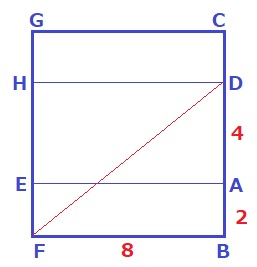
↑上からみた図。
横は８ｃｍ、縦は先ほどの図で言えばＢＯで６ｃｍ。
対角線ＤＦ＝√（８²＋６²＋√21²）
＝√121＝11ｃｍ

②　3.5％!!
Ａと平面ＤＦＬの距離であるＡＭを求めるので、
まず、ＡＭを高さとする立体を見極める。

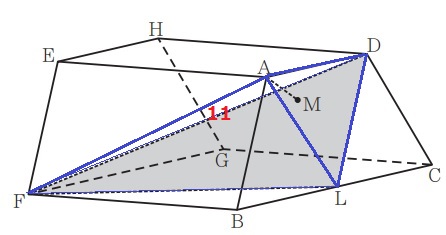
↑三角錐Ｆ－ＡＤＬです。
前問で求めたＤＦも辺に含んでいる。
三角錐Ｆ－ＡＤＬの体積を求め、底辺である△ＤＦＬの面積から高さＡＭを算出する。

長さを認定していく。
ＥＦ//ＡＢ//ＤＬで、四角形ＡＢＬＤは２組の対辺が平行である平行四辺形。
ＢＬ＝４ｃｍ、ＤＬ＝５ｃｍ
△ＦＢＬで三平方→ＦＬ＝４√５ｃｍ

等脚台形ＡＢＣＤの高さは前問で√21ｃｍと求めたので、
三角錐Ｆ－ＡＤＬの体積は、４×√21÷２×８÷３＝16√21/３ｃｍ³

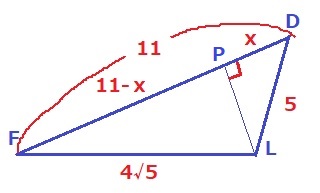
△ＤＦＬの３辺の長さがわかった。
ＬからＤＦに垂線、交点をＰとおく。
ＤＰ＝ｘとすると、ＦＰ＝11－ｘ
２つの三角形で三平方。
ＤＬ²－ＤＰ²＝ＬＰ²＝ＦＬ²－ＦＰ²
５²－ｘ²＝（４√５）²－（11－ｘ）²
25－ｘ²＝80－121＋22ｘ－ｘ²
22ｘ＝66
ｘ＝３

△ＤＬＰは３：４：５の直角三角形→ＬＰ＝４ｃｍ
△ＤＦＬの面積は、11×４÷２＝22ｃｍ²
したがって、ＡＭの長さは、16√21/３×３÷22＝８√21/11ｃｍ

大問１
（５）場合の数。正答率は高かった。
（６）平均。正攻法は方程式だと思うが、算数力が生かせる設問。
（７）整数。こういう形式を経験したか否かで差が大きくでる。
（８）処理系の記述問題。
大問２
（２）②ＥＨを知るにはどこを知るべきか。ゴールから逆算する。
③面積比の処理は手際良く！慣れれば１つの式で答えが求まる。
大問３
（１）②面が離れているのでウッとなるが、２つの面が平行⇒写す。
（２）②決着は立体を見つけられたか否か。
公立高校入試解説ページに戻る