2019年度　秋田県公立高校過去問【数学】解説

平均53.7点

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（15問の中から指示された８問を答える）
（１）　66.3％
５/６×（－0.4）
＝５/６×（－２/５）＝－１/３

（２）　88.6％
２（３ａ－２ｂ）－３（２ａ－ｂ）
＝６ａ－４ｂ－６ａ＋３ｂ
＝－ｂ

（３）　91.3％
６：８＝ｘ：20
内項と外項の積は一緒。
８ｘ＝120
ｘ＝15

（４）　70.7％
（３ｘ＋４）/２＝４ｘ
３ｘ＋４＝８ｘ
ｘ＝４/５

（５）　87.5％
連立方程式。
上の式を２倍して足すのがやりやすいかな？
ｘ＝４、ｙ＝－３

（６）　54.1％
３ｘ²－５ｘ＋２
＝（３ｘ－２）（ｘ－１）＝０
ｘ＝２/３、１

（７）　86.7％
√24－18/√６
＝２√６－３√６＝－√６

（８）　49.6％
傾きが負なので、右下がりの比例。
イ・ウ

（９）　52.9％
本問は有効数字３桁で整数部分が１桁だから6.45を先に書き、
10の累乗で０の数を合わせる。
6.15×10³ｍ

（10）　25.1％！
√ｎは連続する２つの整数（Ｎ、Ｎ＋１）の間にある。
根号が邪魔なので２乗すると、
Ｎ²≦ｎ≦（Ｎ＋１）²
ｎは31個だから、ある平方数から次の平方数までの数の個数が31個となる平方数を見つける。
10²＝100、11²＝121…足りない
12²＝144　13²＝169
14²＝196　15²＝225　16²＝256
256－225＝31！
よって、Ｎ＝15
*平方数は20²まで覚えておくと便利です。

（11）　26.4％！
作図。
∠ＰＢＡ＝30°ということは、∠ＰＢＣ＝60°
60°といえば正三角形。
ＢＣを１辺とする正三角形をつくって、ＡＣとの交点をＰとすればいい。

（12）　73.1％
弧ＢＣに対する中心角ＢＯＣ＝38×２＝76°
△ＯＢＣは二等辺なので、ｘ＝（180－76）÷２＝52°

（13）　77.9％

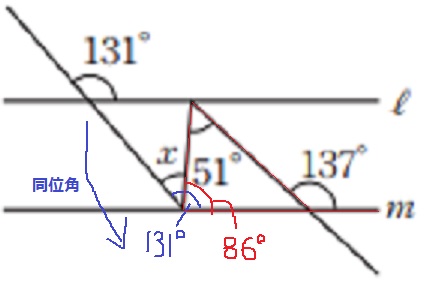
同位角で131°を下し、外角定理から137－51＝86°
ｘ＝131－86＝45°

（14）　41.6％

△ＡＢＨで三平方。
高さＡＨ＝√（９²－３√２²）＝３√７
６×６×３√７÷３＝36√７ｃｍ³

（15）　11.3％！
△ＡＣＤ方向からみる。
面積比は辺の比の２乗なので、
△ＡＣＤ＝④×④＝⑯
△ＡＰＱ＝③×③＝⑨
四角形ＰＣＤＱ＝⑯－⑨＝⑦
三角錐Ａ－ＢＰＱ：四角錐Ｂ－ＰＣＤＱ＝△ＡＰＱ：四角形ＰＣＤＱ＝９：７
よって、９/７倍

大問２（小問集合２）

（１）①　68.9％
過程も記述する。Ａの座標に注目。
ｘ座標が－２、これをｙ＝－12/ｘに放り込む。
ｙ＝６→Ａ（－２、６）
ｙ＝ａｘ²に放り込む。
６＝（－２）²ａ
ａ＝３/２

②　63.8％
ｙ＝－12/ｘから、Ｂ（３、－４）
Ａ（－２、６）→Ｂ（３、－４）
右に５、下に10なので、傾きは－２。
ｙ＝－２ｘ＋ｂに代入して、切片ｂを出す。
ｙ＝－２ｘ＋２　…（イ）

（２）ア（説明）…27.4％！、イ（解答）…36.9％
一次方程式。過程も書かせられる。
枚数をｘとして、代金で等式。
24ｘ＝30×30＋15（ｘ－30）
ｘ＝50　→　50枚

（３）①　78.6％
②のやり方に即した方がやりやすいかな？
板が重なっていないとすると、全体の面積は、４×３×４＝48ｃｍ²
重なりは３ｃｍ²で、４枚だと重なりは３ヶ所あるから、
48－３×３＝39ｃｍ²

②
板１枚の面積
ア…３×４＝12　93.4％
重なりの個数は間の数。
イ…ｎ－１　81.3％
面積を一般化する。
全体の面積から重なりの面積をひく。
ウ…12ｎ－３（ｎ－１）＝９ｎ＋３　39.8％

大問３（平面図形）

（１）①　95.4％
接線の作図手順を解答する。
図２の状態からまず何ができるかを考えていけばたどり着けるかと。
ＡＯを結んで、その垂直二等分線でＭを得て、
Ｍを中心に円を描き、円Ｏとの交点がＰとＱ。
ウ→ア→イ

②　28.9％！
Ａから接点Ｐ、Ｑまでの距離がそれぞれ等しい理由。
△ＡＰＯ≡△ＡＱＯを証明する。
教科書に載っているので正解したい。
共通辺と半径の長さ、接線と半径は垂直に交わることから、
直角三角形の合同条件である斜辺と他の１辺が等しいことを指摘する。

③　9.0％!!
内接円の図形で必ず言えることを選ぶ。
記号選択だが、思考力が試される。勘はダメ×

ア：図ではBA＝BCっぽくもみえるが、仮にそうだとすると△ABCは二等辺となり、
∠BAC＝∠BCAとなるが、その根拠がない。×
イ：悩みどころかな？∠Bは直角とは限らない。
半径でOQ＝OR、Bから接点Q、Rまでの距離が等しい。
△OQBと△ORBは合同（２辺と間の角）となり、OBを対称の軸とした線対称の関係にある。
対応する点QRを結んだ線と対称の軸OBは直交する。○
ウ：AC//QRであれば同位角や錯角が等しくなるはずだが、根拠なし。×
エ：∠OPCと∠ORCは90°。内接する四角形は対角の和が180°なので、
四角形CPORは円に内接する→４点C、P、O、Rは１つの円周上にある。○
イ・エ

（２）　16.7％！
内接円の半径が知りたい。
接線と半径は接点で垂直に交わるので、直角マークをつけていくと・・

四角形SORCとOQBRは４つの角がすべて90°で、縦と横が半径で等しいから正方形。
CR＝RB＝６となり、半径が６ｃｍとわかる。

このあとで手詰る人が多かったか。
全体の面積で方程式を作ろうとしても、右辺と左辺で同じになってしまうので解けない。
角度に注目しよう。

△OAQで、２つの角を○、×とおく。
内角の和から、○＋×＝90°
△DPO≡△DSOから、∠DOP＝∠DOSなので、これらを△とおく。
○＋○＋△＋△＝180°（一直線）だから、○＋△＝90°になる。
○＋×＝90°で○＋△＝90°ということは、×＝△。
ここから、２角が等しいことにより、△OAQ∽△DOPが導ける。
OQ：QA＝DP：PO＝３：６＝１：２
AQ＝６×２/１＝12
△OAQで三平方。AO＝６√５ｃｍ

大問４（データの活用・確率）

（１）①ｘ：94.9％　ｙ：91.7％
ｘ…10～20の人数を数える。１組６人、２組12人だから18。
ｙ…1－（0.1+0.3+0.2+0.05）＝0.35

②　18.2％！
ア。理由も記述する。
30人なので、15人目と16人目の平均値が中央値になる。
１組は20分以上30分未満の階級、２組は10分以上20分未満の階級に、
15人目と16人目の生徒がいる。

（２）　48.5％
答えが負になる式を挙げていく。
（－１）－（＋１）
（－１）×（＋１）
（＋２）×（－３）計３通り。
全体は、２×２×２＝８通り
３/８

大問５（空間図形）

（Ⅰ、Ⅱから指示された問題を答える）
Ⅰ（１）　54.9％
△AFPで、AP＝６、BF＝10
６×10÷２＝30ｃｍ²

（２）　5.5％!!
ABを高さとすると、PFの長さは、
24×２÷10＝4.8
BF＝10－4.8＝5.2
ｘ＝10＋5.2＝15.2

＠公式解答＠
10≦ｘ≦20のとき、FP＝20－ｘ
10×（20－ｘ）×1/2＝24
ｘ＝76/５

（３）ｘ； 0.8%!!!　ｙ；0.0%!!!
BP＋PMが最短→直線
展開図に引きなおす。

相似で、ＦＰ＝10×10/15＝20/３
ｘ＝20＋20/３＝80/３

△ＡＦＰの底辺をＦＰ、高さをＡＦとする。
（辺FGとAF（面AEFB）は垂直）
ＡＦは正方形の対角線なので10√２
ｙ＝20/３×10√２÷２＝100√２/３

Ⅱ（１）　43.9％
４秒後の様子を図示。

ＡＰ：AＱ＝１：２
ＣからＡＢに向けて垂線をひき、交点をHとする。
これは正三角形は真っ二つにする線分なので、
∠ＡＨＣ＝90°であり、30°－60°－90°の直角三角形から、ＡＨ：ＡＣ＝１：２
２辺の比と間の角が等しいから△ＡＨＣ∽△ＡＰＱ
∠ＡＰQ＝∠ＡＨＣ＝90°
△ＡＰＱで三平方→ＰＱ＝４√３
４×４√３÷２＝８√３

（２）　2.5％!!
Ｐは10～15ｃｍ、Ｑは20～30ｃｍ動く。

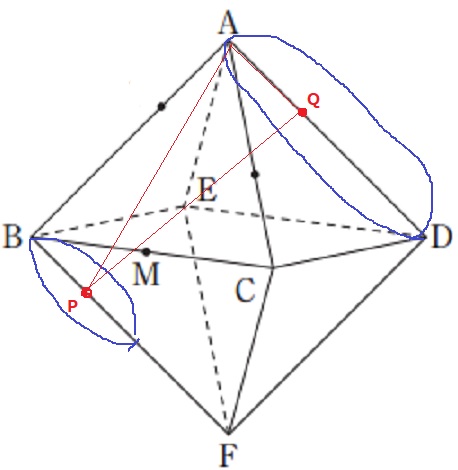
ＰはＢＦ上、ＱはＡＤ上にくる。
ＡＤ//ＢＦで、△ＡＰＱの高さはＡＢ＝10（*四角形ABFDは正方形）
ＡＱ＝24×２÷10＝4.8
Ｑは、30－4.8＝25.2ｃｍ進み、
Ｑの速さは２ｃｍ/秒だから、ｘ＝25.2÷２＝12.6

*正八面体の断面が正方形である理由。

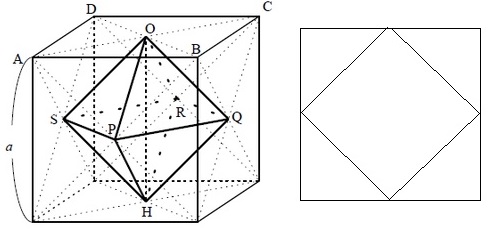
左は城南コベッツより。立方体の各面の中心をつなぐと正八面体になる。
断面は右のように、正方形の中に正方形が現れる。

＠公式解答＠
10≦ｘ≦15のとき、ＡＱ＝30－２ｘ
10×（30－２ｘ）×１/２＝24
ｘ＝63/５

（３）ｘ；0.6％!!!　ｙ；0.0％!!!
まずは位置確認。

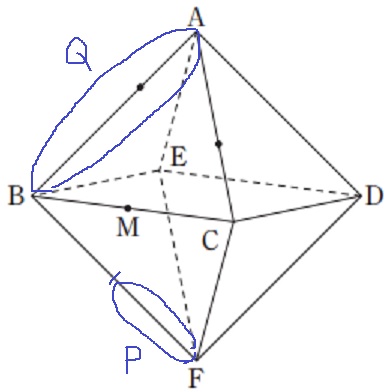
ここらへんのどこかにいる。
△ＡＢＣに注目する。
ＣＱ＋ＱＭの和が最短ということは直線となるが、
ＡＢ上のどこで反射するかわからない。
そこで、ＡＢを対称の軸としてＣを反対側に持ってくる。

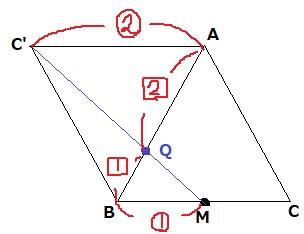
MはBCの中点。
２つの三角形の相似から、AQ：QB＝２：１
AQ＝10×２/３＝20/３
したがって、Qが移動した距離は、30＋20/３＝110/３
Qが毎秒２ｃｍ動くので、ｘ＝110/３÷２＝55/３

ｘ＝55/３から、Pは55/３ｃｍ進んでいる。
BP＝55/３－10＝25/３
PF＝10－25/３＝５/３
BP：PF＝25/３：５/３＝５：１
△APQの面積は、△ABF（正八面体を縦に割ったうちの左半分）で考える。

AFは、正方形AEFCの対角線だから10√２
BCは、AEFCと合同である正方形BCDEの対角線の半分で５√２。
△ABF⇒△ABP⇒△APQ
ｙ＝10√２×５√２÷２×５/６×２/３＝250/９
公立高校入試解説ページに戻る