平均55.5点（前年比±0.0点）
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）ア
√２×√６＋√27
＝２√３＋３√３
＝５√３
イ
（ａ＋２ｂ）/２－ｂ/３
＝｛３（ａ＋２ｂ）－２ｂ｝/６
＝（３ａ＋６ｂ－２ｂ）/６
＝（３ａ＋４ｂ）/６
（２）
√（502－１）
＝√（502－１2） ←平方の差で捉える
＝√｛（50－１）（50＋１）｝
＝√（49×51） ≒√49×√51
＝７√51
（３）ア
ｘ－ｙ＝５ …①
２ｘ＋３ｙ＝－５ …②
①×２－②をして、－５ｙ＝15
ｙ＝－３
①に代入、ｘ＝ｙ＋５＝－３＋５＝２
（ｘ、ｙ）＝（２、－３）
イ
ｘ2＋ｘ－１＝０
解の公式を適用して、ｘ＝（－１±√５）/２
（４）
鉛筆の合計は50ｘ円、ノートの合計は100ｙ円。
これらの和が1000円では足りなかった⇒1000円を超えた。
50ｘ＋100ｙ＞1000
（５）
答案では言葉や数、式を用いて理由を説明する。
平均は面積図で表すことができる。
Ａ10人の平均とＢ11人の平均を長方形で描く。
高さの差が平均の差５分。
Ａに太郎の30分を追加する。30分を10人で均すと平均が＋３点になる。
それでもＢの平均値には届かないので、Ｂ班の平均値が大きい。
↑書き方は公式解答を参照してください。
（６）
答案では言葉や数、式を用いて理由を説明する。
直角三角形であると指摘するには、三平方の定理が成り立てばいい。
２2＋３2＝（√13）2が成り立つから。
（７）
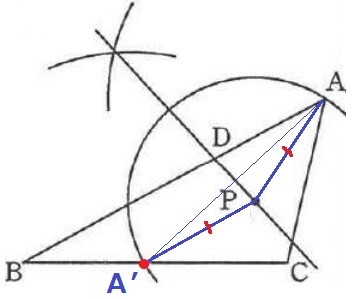
Ｐを通る折り目（対称の軸）で折る。
対応する点は対称の軸上の１点からそれぞれ距離が等しい。
Ａに対応するＢＣ上の点Ａ’は、ＰＡ＝ＰＡ’から位置が求まる。
対応する点を結んだＡＡ’の垂直二等分線が折り目になる。
①ＰＡの長さをとってＢＣに移す。交点がＡ’。
②ＡＡ’の垂直二等分線。これとＡＢとの交点がＤ。
大問２（確率）
（１）
硬貨を２回投げる→２2＝４通り
ＰがＣにくるには【裏】→【裏】しかない（１回目でＣ、２回目は動かない）。
【表】→【表】はＢで止まるので注意！
確率は１/４。
（２）
樹形図で調べる。
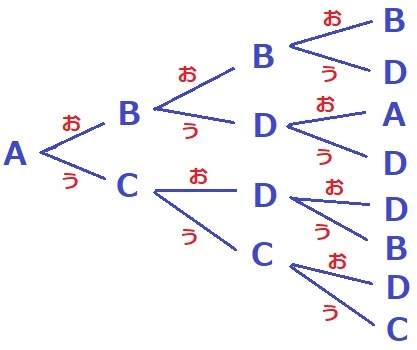
同じ面は連続する。
Ｐが最もあるのはＤ。確率は４/８＝１/２
大問３（方程式）
（１）
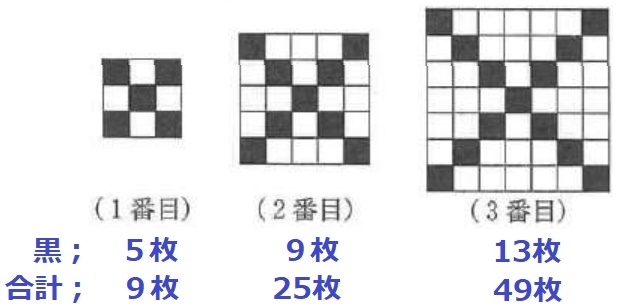
黒を数えると、【５、９、13…】と４ずつ増える。
４番目は17枚、５枚目は21枚。
*四隅が追加されて＋４となる。
（２）
黒の最初は５枚。
４枚ずつ追加される回数はあいだの数だからｎ－１回。
５＋４（ｎ－１）＝４ｎ＋１
すべての枚数は、【９、25、49…】と平方数が連なる。
【３×３、５×５、７×７…】
１、３、５…の奇数は２ｎ－１で表される。
３から始まる数列は、（２ｎ－１）＋２＝２ｎ＋１
ｎ番目が２ｎ＋１、この平方数は（２ｎ＋１）2
黒…４ｎ＋１枚、すべて…（２ｎ＋１）2枚
（３）
答案では言葉や数、式を用いて理由を説明する。
白の枚数が偶数の２乗になることを証明する。
偶数→２ｎだから、（２ｎ）2の形を意識する。
白＝すべて－黒
＝（２ｎ＋１）2－（４ｎ＋１）
＝４ｎ2＋４ｎ＋１－４ｎ－１
＝４ｎ2
＝（２ｎ）2
ｎは整数だから、２ｎは偶数である。
したがって、何番目の図形でも白いタイルの枚数は偶数の２乗になる。
大問４（関数）
（１）
ｙ＝ａｘ2のグラフはａの絶対値が大きくなると、グラフの開きが小さくなる。
ｙ＝１/２ｘ2よりも内側にあるから、ａ＞１/２
イ
（２）ア
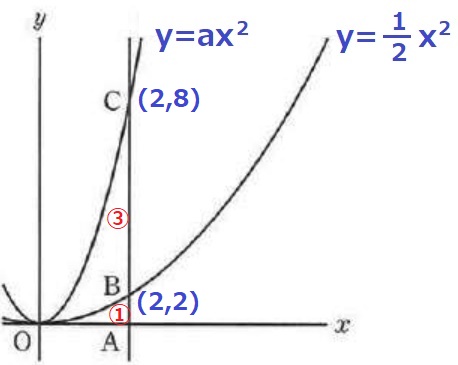
Ｂのｙ座標…ｙ＝１/２ｘ2にｘ＝２を代入、ｙ＝１/２×２2＝２
Ｃのｙ座標…ＡＢ：ＢＣ＝①：③でＡＢ（①）＝２だから、ＡＣ＝２×④＝８
ａの値…ｙ＝ａｘ2にＣ（２、８）を代入、８＝２2ａ、ａ＝２
Ｂ…２、Ｃ…８、ａ…２
イ
ｙ＝２ｘ2において、
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－３のとき、最大値ｙ＝18
０≦ｙ≦18
ウ
ｙ＝１/２ｘ2のｘの変域が－３≦ｘ≦ｂのときのｙの変域が０≦ｙ≦18になった。
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－３のとき、ｙ＝１/２×（－３）2＝９/２
ということは、ｘ＝ｂのとき、最大値ｙ＝18になる。
（ｘ、ｙ）＝（ｂ、18）を代入。
18＝１/２ｂ2
ｂ2＝36
ｂ＞０より、ｂ＝６
（３）
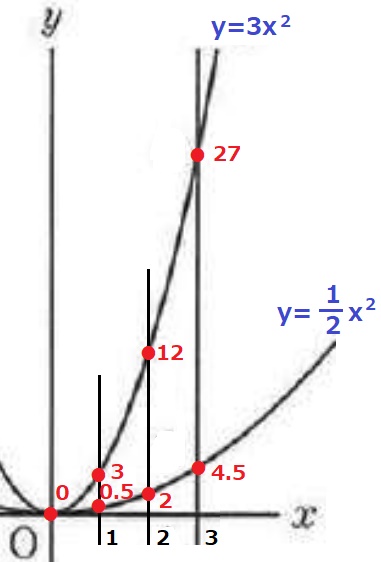
格子点を数える。
ｙ＝１/２ｘ2とｙ＝３ｘ2にｘ＝０～３を代入する。
『図形の周』も含むので原点Ｏを忘れずに！
ｘ＝０のとき、ｙ＝０→１個
ｘ＝１のとき、ｙ＝１～３→３個
ｘ＝２のとき、ｙ＝２～12→11個
ｘ＝３のとき、ｙ＝５～27→23個
１＋３＋11＋23＝38個
大問５（平面図形）
（１）
△ＡＥＤ≡△ＢＤＣの証明。
平行四辺形の対辺は等しい。ＡＤ＝ＢＣ
ＡＢ//ＤＣの錯角から、∠ＡＢＤ＝∠ＢＤＣ
このあとが詰まりやすい。
仮定の∠ＡＢＤ＝∠ＡＥＤから、四角形ＡＢＥＤが等脚台形にみえる…。
ＢとＥはＡＤについて同じ側にあり、∠ＡＢＤ＝∠ＡＥＤであるから、
円周角定理の逆より４点Ａ、Ｂ、Ｅ、Ｄは同一円周上にある。 
弧ＤＥの円周角から、∠ＥＡＤ＝∠ＤＢＣ（×）
△ＡＥＤと△ＢＤＣの残りの内角は等しく、∠ＡＤＥ＝∠ＢＣＤ
１辺と両端角が等しいので合同。
（２）ア
前問の△ＡＥＤ≡△ＢＤＣを使う。
△ＢＤＣ＝９＋★＋16＝25＋★＝△ＡＥＤ
△ＡＤＦ＝25
△ＡＤＦ∽△ＥＢＦの面積比は25：９。
相似比はＡＤ：ＢＥ＝５：３
イ
前問よりＡＤ＝⑤、ＢＥ＝③とする。
平行四辺形の対辺は等しいから、ＢＣ＝⑤
ＥＣ＝⑤－③＝②
△ＡＤＨ∽△ＣＥＨより、ＡＨ：ＨＣ＝⑤：②
Ｇは平行四辺形の対角線の交点。
平方四辺形の対角線はおのおのの中点で交わるので、ＡＣ＝３×２＝６ｃｍ
ＣＨ＝６×②/⑦＝12/７ｃｍ
大問１
（２）筋道は見えやすいが、３問目で驚く。
（５）あまり見かけない記述の形式だが、平均値＋３は＋５に及ばない点を指摘する。
（６）直角三角形の指摘→辺の長さが三平方の関係。√13が斜辺となる。
（７）三角形内部の点Ｐを通る折り目をつくる。正答率は高くなさそう。
折り目は対応する点を結んだ線の垂直二等分線。まず、ＢＣ上にくるＡに対応する点を作図する。
折り目上のＰから等距離にある点と気づきたい。最後にＤを忘れずに！
大問２
（２）条件に合うように調べる。忍耐力を要する。
大問３
（２）３から始まる奇数列は２ｎ＋１、５から始まると２ｎ＋３。
（３）白＝すべて－黒、前問の文字式を用いる。
どんな形が欲しいか想像してから式を変形していく。
大問４
（２）小問が連なる。前半でミスるとドミノ倒しになる。
（３）処理はしやすかった。ｙ＝５～27→27－５＋１＝23個
大問５
（１）正答率は高くなさそう。円周角の定理の逆の形が見えた否か。
（２）ア前問の合同利用は他県でも出題される。共通部分を除外したところが等しい。
イＧが対角線の交点→対角線ＡＣ＝６ｃｍ。チョウチョ相似からＡＨ：ＨＣが出る。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント