2020年度　石川県公立高校入試問題過去問【数学】解説

平均40.0点（前年比；－9.6点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）ア
－３－６
＝－９

イ
７＋（－２³）×４
＝７－８×４
＝－25

ウ
（－３ａｂ）²÷６/５ａ²ｂ
＝９ａ²ｂ²×５/（６ａ²ｂ）　←カッコ内は分母にある
＝15/２ｂ

エ
（ｘ＋３ｙ）/４－（２ｘ－ｙ）/３
＝（３ｘ＋９ｙ－８ｘ＋４ｙ）/12
＝（－５ｘ＋13ｙ）/12

オ
√60×１/√３－√45　←前半は根号同士で約分
＝２√５－３√５
＝－√５

（２）
ｘ²＋５ｘ－３＝０
因数分解ができないので解の公式を適用。
ｘ＝（－５±√37）/２

（３）
『20枚以上余った』→配り終わって余ったａ－５ｂ枚が20以上。
ａ－５ｂ≧20

（４）
ｘ²－ｙ²
＝（ｘ＋ｙ）（ｘ－ｙ）　←ここで代入
＝（√７＋√２＋√７－√２）（√７＋√２－√７＋√２）
＝２√７×２√２＝４√14

（５）
４冊の度数は、１－（0.15＋0.15＋0.3＋0.25）＝0.15
各々の度数と相対度数から平均値を算出。
０×0.15＋１×0.15＋２×0.30＋３×0.25＋４×0.15
＝2.1冊

大問２（確率）

（１）
４枚残る→２枚とる。
約数が２個ということは素数。
２、３、５
*１は素数ではない！

（２）
答案では過程も記述する。
右端は偶数の６なので、右端が奇数になるには６と奇数のどれかを交換するしかない。
（１、６）（３、６）（５、６）これらの逆を含めて６通り。
全体は６×６＝36通り。偶数になる場合は、36－６＝30通り
確率は30/36＝５/６

大問３（関数）

（１）
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－３のとき、最大値ｙ＝９
０≦ｙ≦９

（２）

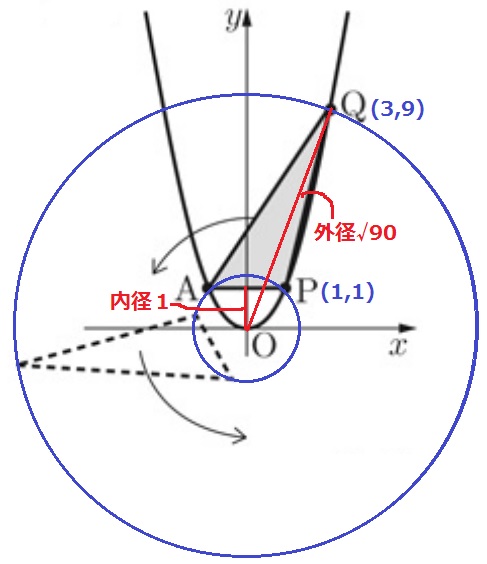
このようなドーナッツ型になる。
外径はＱ座標から、√（９²＋３²）＝√90
内径はＯＡ・ＯＰでないことに注意！
Ｏを中心にＡＰを回転させると、ＡＰとＯの距離にあたる１が内径。
（√90）²π－１²π＝89π

（３）
答案では過程も記述する。

おなじみの等積変形。
Ｒのｘ座標が負なので、上図のようにＱを直線ＯＡ上に持ってくる。
Ａ（－１、１）→Ｐ（３、９）
右に４、上に８だからＡＰの傾きは２。

ＲＱの式を求める。
傾きは２、Ｑ（４、16）を通るので、
16＝２×４＋ｂ
ｂ＝８
ｙ＝２ｘ＋８

Ｒはｙ＝２ｘ＋８とｙ＝－ｘの交点。
２ｘ＋８＝－ｘ
ｘ＝－８/３
したがって、Ｒ（－８/３、８/３）

大問４（方程式）

答案では過程も記述する。
求めたいものを文字に置く。
2008年度、2018年度の３種類のゴミの排出量の合計をそれぞれｘ、ｙとする。
排出量の合計の比較から、ｘ－ｙ＝225…①
燃えないゴミの排出量の比較から、
0.08ｘ：0.04ｙ＝10：４　←６割減＝４割
内項と外項の積で0.32ｘ＝0.4ｙ
４ｘ＝５ｙ…②

①×４
４ｘ－４ｙ＝900
②より、４ｘに５ｙを代入。
５ｙ－４ｙ＝ｙ＝900
②に代入。４ｘ＝５×900
ｘ＝1125

2008年度の３種類のゴミの排出量の合計…1125ｇ
2018年度の３種類のゴミの排出量の合計…900ｇ

大問５（作図）

①∠ＡＢＰ＝∠ＣＢＰ→∠ＡＢＣの二等分線
∠ＡＢＰ＝∠ＰＢＣに置き換えると少しわかりやすくなるかも。
②∠ＡＤＣ＝∠ＡＰＣ→弧ＡＣに対する円周角で等しくなる→Ａ・Ｄ・Ｃを通る円の作成。
ＡＤとＣＤの垂直二等分線を描き、その交点が円の中心となる。
③二等分線と円周の交点がＰ。

大問６（平面図形）

（１）

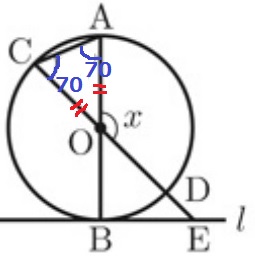
半径で△ＯＡＣは二等辺。
△ＯＡＣで外角定理→ｘ＝70＋70＝140°

（２）
答案では過程も記述する。

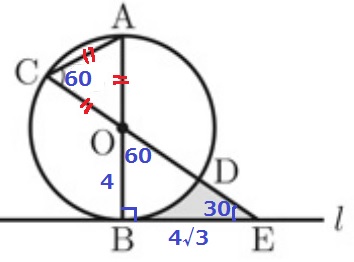
与えられた60°から有名三角形に気づきやすい。
△ＡＯＣは正三角形。

∠ＢＯＥ＝60°
直径ＡＢと接線ℓは垂直。
△ＯＢＥは30°－60°－90°で辺の比が１：２：√３
△ＯＢＥから扇形ＯＢＤを引く。
４√３×４÷２－４×４×π×60/360
＝８√３－８/３πｃｍ²

（３）
△ＣＰＥ∽△ＱＤＥの証明。
辺の情報が乏しいので角度攻め。

共通角から∠ＣＥＰ＝∠ＱＥＤ（★）
直径ＡＢと垂線ℓは垂直、直径ＣＤに対する円周角ＣＡＤ＝90°
直角三角形ＡＢＰとＣＡＤをうまく利用する。
△ＡＢＰで∠ＡＰＢ＝●、ＰＡＢ＝×とおく。
●＋×＝90°から、∠ＯＡＤ＝90－×＝●
また、半径から△ＯＡＤは二等辺で∠ＯＤＣ＝●
対頂角でＱＤＥ＝●
２角相等で∽。

大問７（空間図形）

（１）
ネジレ→延長しても交わらない、かつ平行でもない。
辺ＡＣ

（２）
答案では過程も記述する。

△ＡＢＤで三平方→ＡＤ＝３√３ｃｍ
△ＡＢＣと△ＯＢＣは合同な正三角形で、
底辺をＢＣとすると、高さはＡＤ＝ＯＤで等しい→△ＯＡＤは二等辺三角形。
ＤからＡＯに向けて垂線、交点ＥはＡＯの中点だからＡＥ＝３ｃｍ
△ＡＥＤで三平方→ＤＥ＝３√２ｃｍ
△ＯＡＤの面積は、６×３√２÷２＝９√２ｃｍ²

（３）
ここも過程を記述する。

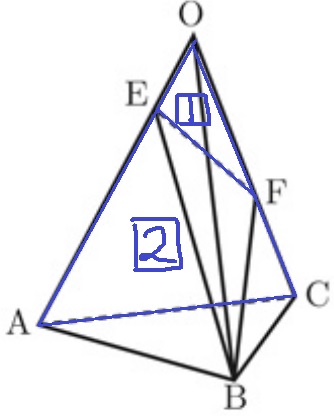
△ＯＡＣを底面に捉えよう。
三角錐Ｂ－ＯＥＦと四角錘Ｂ－ＥＡＣＦの体積比が１：２
これらは高さが等しいので、底面の△ＯＥＦと四角形ＥＡＣＦの面積比が１：２
△ＯＥＦの面積を【１】とすると、△ＯＡＣの面積は【３】

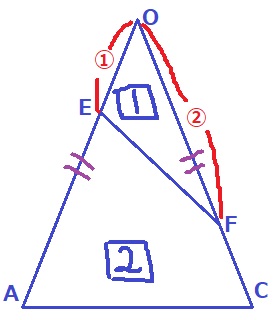
隣辺比から、△ＯＥＦ＝①×②＝〔２〕＝【１】
（辺の比が〇。辺の比の２乗の面積が〔　〕。これを【　】と比較）
△ＯＡＣの面積は【３】だから〔６〕
△ＯＡＣは二等辺なので、ＯＡ×ＯＣ＝〔６〕
ＯＡ＝ＯＣ＝〇√６

ＯＡ＝８ｃｍだから、
ＯＥ＝８×①/〇√６
＝４√６/３ｃｍ