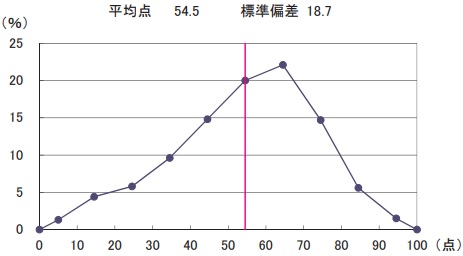
平均54.5点(前年比;-4.0点)
問題はこちら→リセマムさん
大問1(計算)-85.5%
(1) 97.7%
15÷(-3)
=-5
(2) 91.0%
7-(-3/4)×(-2)2
=7-(-3/4)×4
=7+3=10
(3) 87.8%
(7x+y)-4(1/2x+3/4y)
=7x+y-2x-3y
=5x-2y
(4) 74.0%
9a+3b=2
3b=-9a+2
b=-3a+2/3
(5) 87.9%
4/√2-√3×√6
=2√2-3√2
=-√2
(6) 74.3%
2x2+x-4=0
解の公式を適用。
x={-1±√(12-4・2・(-4)}/2・2
x=(-1±√33)/4
大問2(小問集合)-50.6%
(1) 76.7%
レンジ(range)は範囲。〔最大値-最小値〕で求める。
178.2-163.5=14.7cm ウ
(2) 44.6%
x=1のとき、y=12
x=4のとき、y=3
変化の割合…(yの増加量)/(xの増加量)=(3-12)/(4-1)=-3
反比例はxが増えるとyは減るので、変化の割合はマイナスになる。
(3) 61.2%
買ったゼリーの個数をxとおくと、プリンの個数は24-x個。
80x+120(24-x)+100=2420
40x=560
x=14 → 14個
(4) 41.6%
aで+(右)、bで-(左)
絶対値が2以下→計算結果が-2以上2以下。
式に表してみよう。
〔2+a-b=2〕
a-b=0
aとbが同数になればOK。6通り
〔2+a-b=1〕
a-b=-1
b-a=1 ←両辺に-をかけてます
b>aで、bとaの差が1。5通り
〔2+a-b=0〕
a-b=-2 (b-a=2)
b>aで、bとaの差が2。4通り
〔2+a-b=-1〕
a-b=-3 (b-a=3)
法則が見えてきた( ✧Д✧) 3通り
〔2+a-b=-2〕
a-b=-4 (b-a=4)2通り
計20通り 確率は、20/36=5/9
法則がわかると後半はスラスラいける。
(5) 28.9%!
作図がやりやすくなってる。
Aは半直線OX上にあり、Bは半直線OY上にある。
OA=OBなので、AとBはOから等距離にあるが、
直線ABがPを通過しなければならない。
そこで、∠XOYの二等分線を描き、これとPを通る垂線を作図する。

↑イメージとしてはこんな感じ。
青が∠XOYの二等分線。
二等分線に対する垂線(赤い線)で、
OXとの交点とOYとの交点は、共にOからの距離が等しくなる。
(理由は二等分線を対称の軸としたとき、2つの三角形が左右対称になるから。
●が角の二等分、1つが垂直なので、残りの角●も等しい。
共通辺―より、1辺と両端角が等しい→左右の三角形が合同)
この線がPを通れば良い。
①∠XOYの二等分線
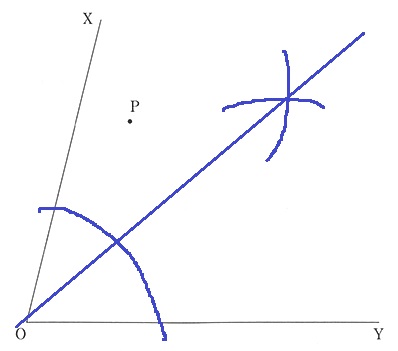
②Pを通る垂線。

AとBの記載もお忘れなく!
大問3(関数)-51.9%
(1) 85.5%
A(2、2)をy=ax2に放り込む。
2=22a
4a=2
a=1/2
(2)① 63.6%
y=1/2x2からB座標は(6、18)
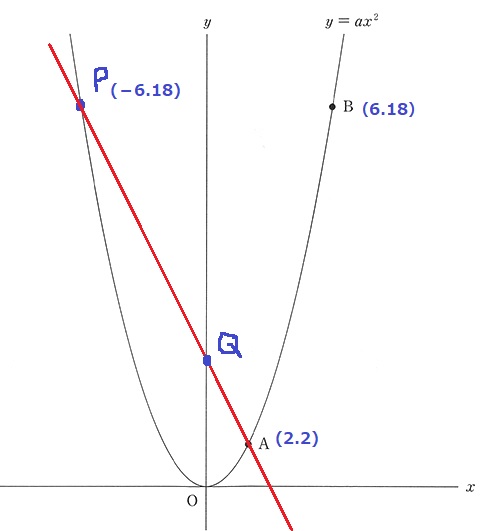
P→Qと作成。
PAの式を求める。
右に8、下に16なので、傾きは-2。
A(2、2)をy=-2x+bに代入。
2=-2×2+b
b=6
PA;y=-2x+6の切片がQのy座標なので6。
② 6.7%!!
面積の二等分なので等積変形だろうと予測はつくが、どう使うかが問題。
まず、△ABQと面積の等しい三角形を考える。
ポイントはPA上。
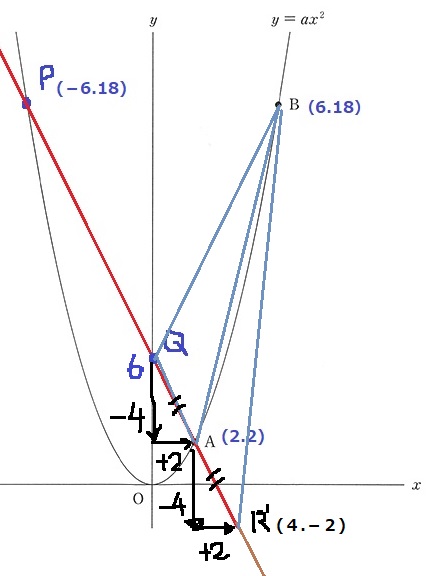
底辺の長さが同じであれば、面積も同じ。
QAと同じ長さで、AR’を描く。
R’の座標は、Q→Aが下4、右2なので、
A→R’もAから下4、右2に移動してR’(4、-2)
R’をx軸に移行する。
ここで等積変形を使う。
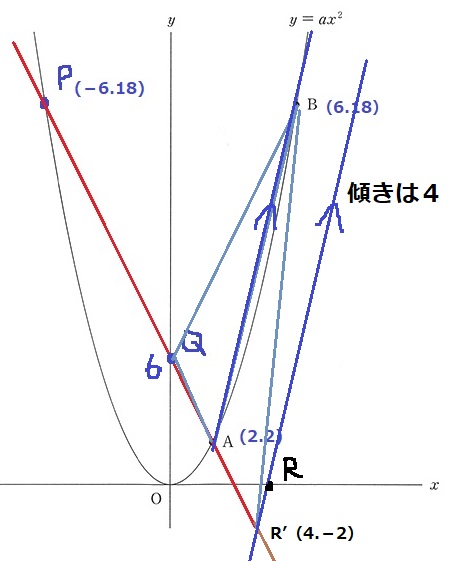
ABの傾きは、右に4、上に16だから4。
R’Rも平行で同様。R’の座標から、
-2=4×4+b
b=-18
y=4x-18
Rのx座標は、この式でy=0のとき、
0=4x-18
x=18/4=9/2
いきなりx軸に注意を向けるのでなく、迂回しよう。
大問4(平面図形)-46.2%
(1)
はじめはPQ//DCを導くために、【四角形PQCDが平行四辺形】であることを証明する。
a…PDに等しいのはQCしかない。 イ 98.0%
b…②と③をみると、1組の対辺が等しくて平行。カ 76.0%
平行四辺形の合同条件も確認しておこう。
c…△RQE∽△SGFの証明。 6点-10.6%! 3点-6.4% 無答-40.3%!!
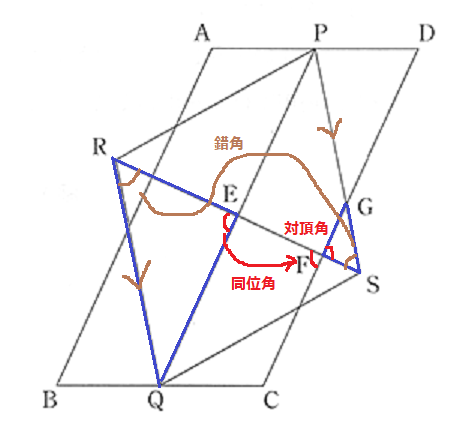
青く囲った2つの三角形の関係に注目。
先ほど、PQ//DCを出したので、これを利用して同位角→対頂角。
さらに、ひし形は特殊な平行四辺形なので、
RQ//PSから錯角。2角が等しいので、∽。
② 0.2%!!!
抜け毛がでるほどの鬼問。
菱形の1辺が5cmなので、GSは2cm。
菱形ばかりいじっていると迷子になる。
ポイントは、平行四辺形の1辺の半分であるPD=2cmをうまく使う。
Sを通るADに平行な線分を引き、CDとの交点をHとする。
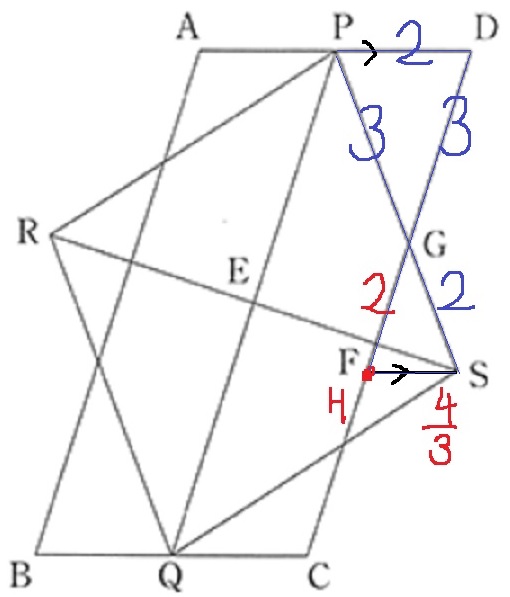
△GDPと△GHSは相似(錯角や対頂角で2角が等しい)。
PG:SG=3:2から、
GH=2、HS=4/3
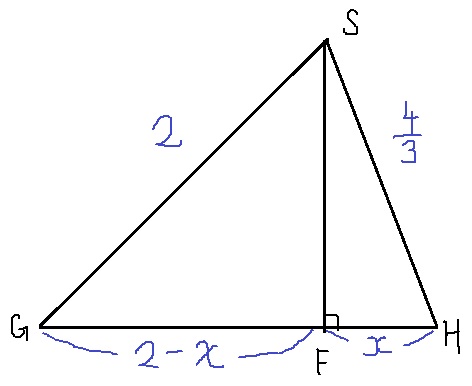
△SGHをピックアップ。
菱形の対角線は垂直に交わり、PQ//DCだから、
GHとSFは垂直に交わる。
あとはお決まりの三平方。
22-(2-x)2=(4/3)2-x2
-x2+4x=-x2+16/9
4x=16/9
x=4/9
△SFH内で三平方。
FS2=(4/3)2-(4/9)2
=128/81
FS=√(128/81)=8√2/9cm
キツイね(´゚д゚`)
平行四辺形と菱形の融合なので、菱形でダメだったら、
どこかで菱形と平行四辺形を組み合わせられないか、という発想に飛ばす。
*最後の方の分母が誤っていました。ミスのご指摘ありがとうございました。
大問5(空間図形)-31.3%
(1)① 63.5%
円錐の体積。
6×6×π×6×1/3=72πcm3
② 33.0%!
球をボチャっと入れたときに、球が水面をはみ出ないかを判定。

断面を作図するとこんな感じ。
大きい直角二等辺三角形を縦に切断すると、左右に直角二等辺三角形。
円の中心から半径を描き、接線は垂直。
すると、1辺2cmの正方形が現れる。
この対角線は1:1:√2から、2√2cm。
√2は一夜一夜に人見ごろ…(1.4142…)
球の上部は、2+2×1.4142…<6cmなので、
球はすべて水に沈む。
あふれた水の体積=球の体積(4/3πr3)
4/3π×23=32/3πcm3
(2)4点-18.7%! 3点-6.0% 無答-29.7%
公式解答参照。
AとBの体積を求めて比べるだけ。
Aは円錐、Bは円柱から半球を引く。
すると、ともに125/3πcm3で値が同じになるので、水はあふれない。
半球の体積は円柱の2/3にあたることになる。
(3) 6.9%!!
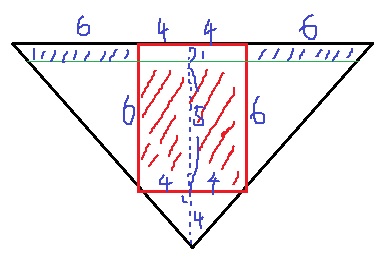
おもりの半径4cmを手がかりに、おもりの底面と容器の最深部の距離は4cm。
おもりの高さは、10-4=6cm
おもりが沈んだ部分(赤斜線)から、まだ水が満たされていない(青斜線)を引き、
超過分があふれ出た水の体積になる。
青斜線はr=10とr=9の体積比103:93で計算して、
容器A全体を103とおき、水のない1cm分は(103-93)とする。
ここからおもりがある部分を引くことに注意!
赤斜線…4×4×π×5=80πcm3
青斜線…10×10×π×10×1/3×(103-93)/103-4×4×π×1
=271/3π-16π=223/3πcm3
80π-223/3π=17/3πcm3
@別解@
光宮百吉子さんから素晴らしい解法を頂きました。
【あふれ出た水の体積=9cmの円錐+円柱-10cmの円錐】
=9×9×π×9×1/3+4×4×π×6+10×10×π×10×1/3
=243π+96π-1000/3π
=17/3πcm3
9cmの円錐(形が変わる水)におもりを沈めるとき、
水があった空間におもりが入ってきますが、同じ空間にこれらは重複しません。
9cmの円錐の水と円柱のおもりの体積の和は、
10cmの円錐の容器と溢れ出た水の体積の和に相当するので上の式が成り立ちます。
こちらの方が式がスッキリして計算処理が楽ですね!
2019年度(千葉)前期
社会…平均56.6点 理科…平均60.6点 英語…平均53.6点 国語…平均54.2点
2019年度(千葉)後期
数学…平均61.0点 社会…平均65.8点 理科…平均61.6点 英語…平均61.9点 国語…平均59.2点
その他は下記のリンクの目次からどうぞです。



コメント
大問4の2
△PGDの面積は三平方の定理を使って、底辺2、高さ2√2なので、2×2√2×1/2=2√2
△PGD∽△SGHで相似比は3:2で面積比は9:4、△SGHの面積は2√2×4/9=8√2/9
また△SGHの面積は底辺GH、高さFSになるので 2×FS×1/2=8√2/9
FS=8√2/9cm
別解
上記で△PGDの高さを求めるときに使った 3:1:2√2の三角形と△FHSが相似となる
またHSが4/3cmなので、FS:2√2=4/3:3 これを解いてFS=8√2/9
大問5(3)
同じことをしているのかもしれませんが、単純に最初に入っていた水の体積から最後に入っている水の体積を引きます
最初に入っていた水の体積=9x9xπx9x(1/3)=243π
最後に入っている水の体積=10x10xπx10x(1/3)ー4x4xπx6=(712/3)π
溢れた水の体積=243πー(712/3)π=(17/3)π