平均55.8点(前年比;+7.8点)
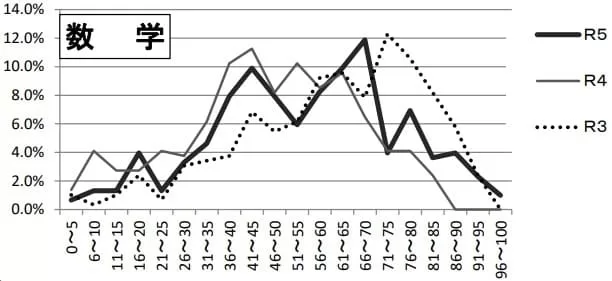
問題はこちら→東進ハイスクールさん(解答)
大問1(小問集合)
(1) 97.7%
7x-3x
=4x
(2) 94.4%
4×(-7)+20
=-28+20
=-8
(3) 91.7%
30xy2÷5x÷3y
=2y
(4) 82.8%
1.3x+0.6=0.5x+3 ←両辺10倍
13x+6=5x+30
8x=24
x=3
(5) 85.1%
8/√2-3√2
=4√2-3√2
=√2
(6) 91.4%
x2-11x+30
=(x-5)(x-6)
(7) 86.8%(一部正答1.0%)
3x+5y=2 …①
-2x+9y=11 …②
①×2+②×3をすると、37y=37
y=1
①に代入、3x+5×1=2
x=-1
x=-1、y=1
(8) 78.9%
3x2-5x-1=0
解の公式を適用して、x=(5±√37)/6
(9) 76.2%(一部正答8.9%)
全数調査は調査対象すべてを調べ上げる。
標本調査は母集団のなかから標本を無作為に抽出して、母集団の様子を推し量る。
総務省統計局が5年に1度行う国勢調査は全数調査の代表例。
国の基礎的な統計資料として国策の判断に使われる。
健康診断も個々人のデータをとらなければ意味がないので全数調査。
河川の水質調査とテレビの視聴率は一部を調べる標本調査。
ア・ウ
@テレビの視聴率@
標本(サンプル)の大きさはどの程度求められるか。
大学レベルの統計学の知識が求められると思うのでサボにはわかりませんが、
視聴率を計測する機器が設置されているテレビの台数は、
全体の0.01%にも満たないようですw( ゚Д゚)w
視聴率調査に協力している人を全く見掛けない理由(ねとらぼ)
↑この記事によると、2017年10月時点で調査対象世帯は全体の0.00005%以下となっている…。
それだけで残りの99.999…%以上を推し量って良いものなのか疑問に思われますが、
統計学的には十分信頼するに足りるサンプル数なんだとか。
どうやら母集団が大きくなるほど、標本の大きさは思ったより小さくても間に合うようです。
反対に母集団が小さいと(例えば1つのクラスの動向では)多くの標本をとらなければならない。
(10) 49.8%
y=6/xにそれぞれのx座標を代入する。
A(-6、-1)→B(2、3)
右に8、上に4移動するので、傾きは4/8=1/2
Bから左に2、下に1移動して、切片は3-1=2
y=1/2x+2
(11) 42.6%
y=2x2はa>0で下に凸のグラフ。
x=0のとき、最小値y=0→aは少なくとも0以下(a≦0)
x=1のとき、y=2だから、x=aのときにy=18になる。
18=2x2
x=±3
a≦0より、a=-3
(12) 56.8%

ADとBCを均すとEFに相当する。
(5+8)÷2=13/2cm
(13) 44.6%
3枚の硬貨を投げた結果は、23=8通り
100円玉が表になれば100円以上になるので、余事象で考えてみる。
100円未満は〔3枚すべて裏〕〔2枚の50円玉のうち1枚が裏〕の3通り。
100円以上は5通りで、確率は5/8。
*誤答は1/2が多かった。
(14) 8.3%!!
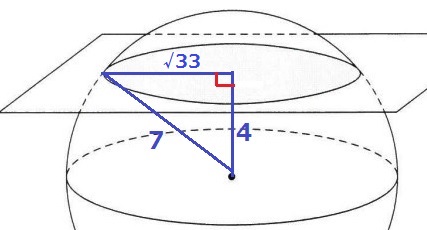
断面の円の半径は、三平方から√(72-42)=√33cm
断面の円の面積は、√33×√33×π=33πcm2
(16) 45.5%(一部正答9.9%)
説明問題。
18人の第2四分位数(中央値)は9番目と10番目の平均。
第1四分位数は下位9人の真ん中、下から5番目。(問題文より20~30分の階級)
第3四分位数は上位9人の真ん中、上から5番目。
ヒストグラムの第3四分位数は40分以上50分未満の階級に含まれるが、
イでは50分以上60未満の階級に含まれるので誤り。
大問2(作図・整数)
(1) 34.7%(一部正答21.1%)
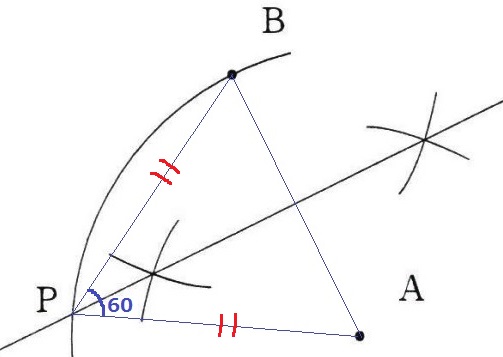
AとBは円周上の2点。
Aが反時計回りに回転移動した点がBだから、
回転の中心PはABの垂直二等分線上の左側にある。
Aは15×4=60°動くので、∠APB=60°
半径でPA=PB→△PABは正三角形
AB=APより、ABの長さを垂直二等分線上にもってきた交点がP。
(2) 21.5%!(一部正答13.9%)
整数の証明問題。
Xの十の位をa、一の位をyとする。
X=10a+b、Y=10b+a
X+Y
=(10a+b)+(10b+a)
=11a+11b
=11(a+b)
a、bは整数なのでa+bも整数。
したがって、XとYの和は11の倍数になる。
大問3(整数)
(1) 40.6%(一部正答22.4%)
●偶数の中では唯一、n=6のときだけ0.16666…と無限小数が起きている。
●1桁の奇数では5が有限小数だった。2桁の奇数において5の倍数に絞って考える。
問題文では20と32のあいだにイがあり、この範囲にある5の倍数の奇数は25しかない。
1/25=4/100=0.04(←有限小数)
ア…6、イ…25
(2) 52.1%
1÷7=0.1428571428…
〔142857〕がループする。
この6個の数を1周とすると、50÷6=8…2
50番目は8周+2個。
最後の2は1と4→50番目は4
大問4(空間図形)
(1) 29.4%!

最短距離なので、展開図を作成。
△IEG∽△PFGより、PF=2×4/8=1cm
BP=6-1=5cm
Pは秒速1cmだから5秒後。
(2) 7.6%!(一部正答18.2%)
△APCが二等辺三角形である証明。
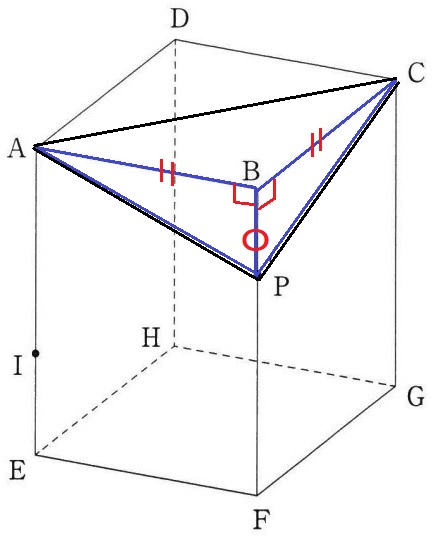
△APCが二等辺である→PA=PCを証明すればいい。
△ABPと△CBPに着目する。
共通辺BP
仮定から、AB=CB、∠ABP=CBP
2辺とあいだの角が等しいから、△ABP≡△CBP
対応する辺からPA=PCが成り立ち、△APCは二等辺三角形である。
@余談@
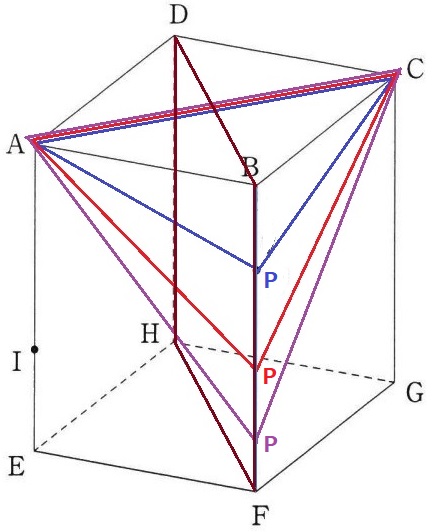
BF上にあるPがどこにいても、△APCは二等辺三角形になる。
(面DHFBを対称面に左右対称)
(3) 5.0%!!
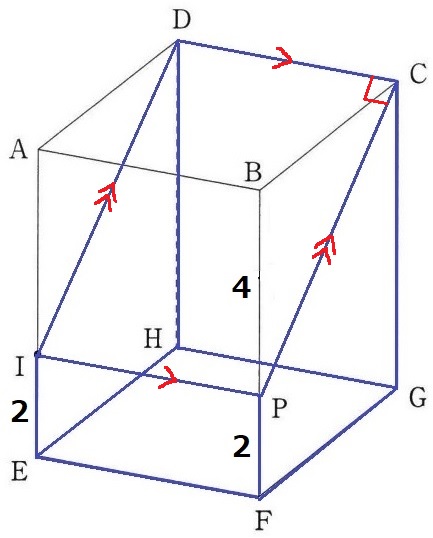
↑4秒後の様子。IE=PF=2cm
断面の四角形の対辺は平行。
DC⊥面BFGC→PCは面BFGC上の線分でDC⊥PC
2組の対辺が平行で内角の1つが直角。四角形DIPCは長方形である。
下の大きい立体の表面積を求める。
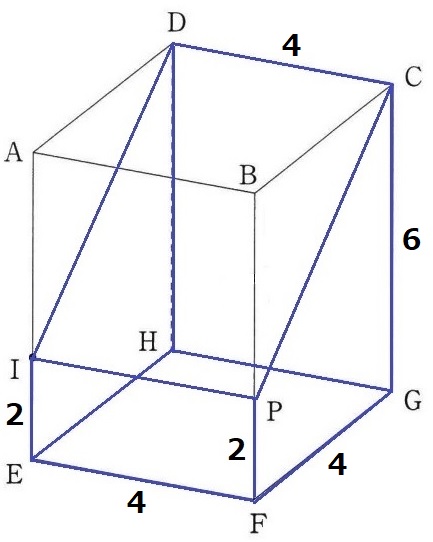
先に長方形DIPC以外を求める。
4×4+2×4+(2+6)×4÷2×2+4×6=80cm2
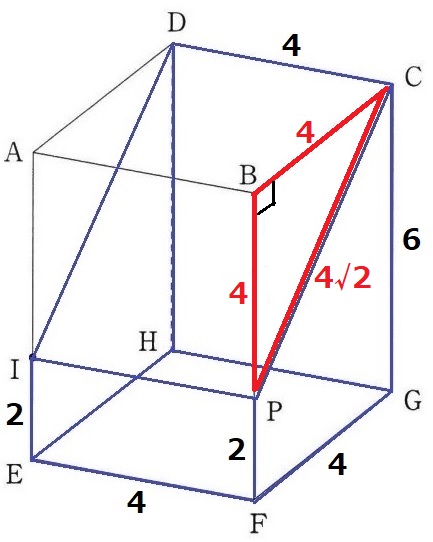
△BPCは直角二等辺三角形。
1:1:√2より、CP=4√2
長方形DIPC=4×4√2=16√2cm2
したがって、求積すべき立体の表面積は80+16√2cm2
●講評●
大問1
ここだけで配点が65点もある。
(10)までは確実にとっておきたい。
(11)問題集によくある形式だが、実力差がでやすい。
y=0を含むということは原点を通過する。x=aのときy=18から立式。
(12)模範的な説明としてはAを通るDCに平行な線をひき、5cmを下に降ろす。
左側で中点連結定理→5+3÷2=13/2cm
(14)円や球の問題は半径が糸口になる。
(15)1個ずつ書くと確実。
(16)第3四分位数は上から5番目。ヒストグラムとイの箱ひげ図では階級が異なる。
大問2
(1)題材が理科でおもしろい(‘ω’)
北の空では北極星を中心に反時計回りに動く。
Aは60°の回転移動→△PABは正三角形。
大問3
(1)イ問題文のヒントがありがたすぎる。
(2)規則の基本問題なので解けて欲しい。
大問4
(2)それを証明するには何を指摘すれば良いか。出だしが肝心。
(3)それほど難しくはない。
断面はDを通り、四角形DIPCは長方形。それぞれの面積を足し合わせる。




コメント