平均48.6点（前年比；＋8.6点）
問題はコチラ→ＰＤＦファイル
出題範囲の削減はなし。
大問１（小問集合）
（１）ア
６－（－１）
＝６＋１
＝７
イ
（－２）2－５×３
＝４－15
＝－11
ウ
９/４ｘｙ3÷３/２ｘｙ
＝３/２ｙ2
エ
（４ａ＋ｂ）/９－（ａ－２ｂ）/３
＝｛（４ａ＋ｂ）－３（ａ－２ｂ）｝/９
＝（４ａ＋ｂ－３ａ＋６ｂ）/９
＝（ａ＋７ｂ）/９
オ
√32＋２√３÷√６
＝４√２＋√２
＝５√２
（２）
反比例の比例定数ａは積ｘｙで一定。
ａ＝３×２＝６
ｙ＝６/ｘ
（３）
４＜√ｎ＜５ ←２乗
16＜ｎ＜25
ｎ＝17～24の８個
（４）
球の表面積Ｓ＝４πｒ2
半球なのでこれの半分。さらに、下の円を足す。
４π×３2÷２＋３×３×π
＝27πｃｍ2
（５）
ア：最頻値（モード）は１匹。×
イ：平均値は、（０×２＋１×４＋２×１＋３×３＋４×１＋５×１）÷12＝２匹×
ウ：12匹の中央値（メジアン）は６番目と７番目の平均→1.5匹〇
エ：範囲（レンジ）は、最大値５－最小値０＝５匹×
ウ
大問２（確率）
（１）
３つの順列。
3Ｐ3＝３×２×１＝６通り
（２）
答案では理由も記述する。ｐとｑの確率を比較すればいい。
◆ｐの確率
４個から２個取り出す。4Ｃ2＝６通り
赤玉を取る組み合わせは（赤、①）（赤、②）（赤、③）の３通り。
ｐ＝３/６＝１/２
◆ｑの確率
１個ずつ取り出すので、全体は４×４＝16通り
【全体－２回とも白玉＝少なくとも１個は赤玉】
少なくとも１個は赤玉…16－３×３＝７通り
ｑ＝７/16
１/２＞７/16ゆえ、ｐの方が大きい。（ア）
＠別解＠
ｐの確率について。１回目に赤が出る確率は１/４。２回目は何でもいい。
１回目が白⇒２回目で赤が出る確率は、３/４×１/３＝１/４
合計して１/２
大問３（数量変化）
（１）
ｙ＝ａｘ2の形だから、
ｘの値が３倍になると、ｙの値は９倍になる。
（２）
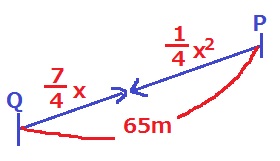
出会った時間をｘ秒後とすると、うえのようになる。
距離で等式。
１/４ｘ2＋７/４ｘ＝65 ←４倍して整理
ｘ2＋７ｘ－260
＝（ｘ－13）（ｘ＋20）＝０
ｘ＞０ゆえ、ｘ＝13
13秒後
（３）
答案では途中の計算も書く。
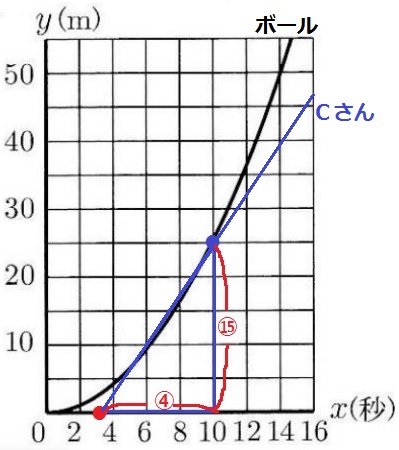
10秒後に追い越されるから、（10、25）の点を通る。
毎秒15/４ｍの速さ→傾きが15/４→右に④、上に⑮の傾き。
⑮＝25ｍだから、④＝25×④/⑮＝20/３
Ｃが出発したのは、10－20/３＝10/３秒後
大問４（方程式）
答案では途中の計算も書く。
大きいプランターをｘ個、小さいプランターをｙ個とする。
プランターの個数で等式。ｘ＋ｙ＝45…①
大きいプランターには６個ずつ、小さいプランターには４個ずつ植える。
（最初はスイセンとチューリップを区別しないで考える）
６ｘ＋４ｙ＝216 …②
②－①×４
２ｘ＝36
ｘ＝18
①に代入して、ｙ＝27
大きいプランターが18個、小さいプランターが27個。
チューリップは小さいのに２個ずつ植えたから、２×27＝54個
スイセンは、216－54＝162個
スイセン…162個、チューリップ…54個
大問５（作図）
②∠ＰＡＢ＝１/２∠ＣＡＢより、
∠ＣＡＢの二等分線上のどこかにＰがある。
③ＡＰ＝√２ＡＢ
ＡＰ：ＡＢ＝√２：１
√２とくれば直角二等辺三角形の斜辺。
ＡＢを直角二等辺の等辺としたとき、Ａから斜辺の長さだけ離れたところにＰがある。
Ｂを通る直線ｌの垂線をひき、ＡＢ＝ＢＰ’となるようなＰ’をとる。
直角二等辺三角形ＡＢＰ’において、ＡＰ’：ＡＢ＝√２：１
あとはＰ’を∠ＣＡＢの二等分線上に乗せればいい。
ＡＰ’＝ＡＰとなるように移動させる。
大問６（空間図形）
（１）
Ｂと重なるのはア・エ
（２）
△ＯＥＦ∽△ＯＡＢを活用する。
ＯＥ：ＥＡ＝１：３だから、ＥＦ＝①とするとＡＢ＝④
底面積の比は、正四角錐：直方体＝④×④：①×①＝16：１
高さの比は、正四角錘：直方体＝ＯＡ：ＥＡ＝４：３
体積比＝底面積の比×高さの比
錘は÷３すること！
正四角錘：直方体＝（16×４÷３）：（１×３）
＝64/３：３
＝64：９
（３）
答案では途中の計算も書く。
△ＢＰＱは直角二等辺三角形。
辺の比は１：１：√２だから、ＰＱ＝２√２ｃｍ
ＲＰ＝２√２ｃｍとなる。
△ＯＡＢで考えてみよう。
こういう求めにくい図形は有名角を疑う。
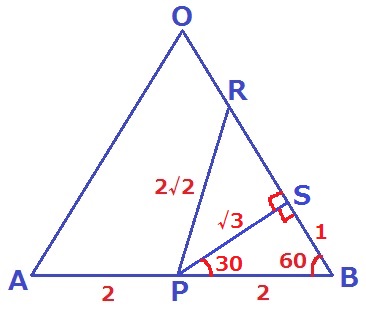
ＰからＢＲに垂線、足をＳとする。
△ＢＰＳの内角は30°－60°ー90°で辺の比は１：２：√３の直角三角形。
ＰＳ＝√３ｃｍ、ＳＢ＝１ｃｍ
△ＰＲＳで三平方→ＲＳ＝√５ｃｍ
したがって、ＲＢ＝１＋√５ｃｍ
大問７（平面図形）
（１）
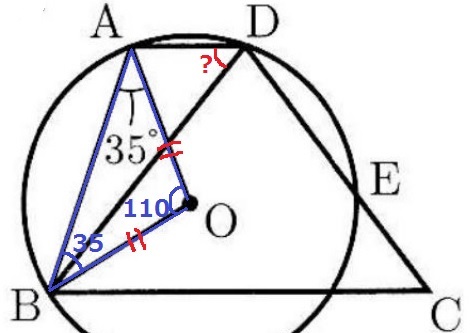
半径より、△ＯＡＢは二等辺。
∠ＡＯＢ＝180－35×２＝110°
∠ＡＤＢは弧ＡＢに対する円周角だから、110÷２＝55°
（２）
△ＡＢＥ∽△ＤＣＢの証明。
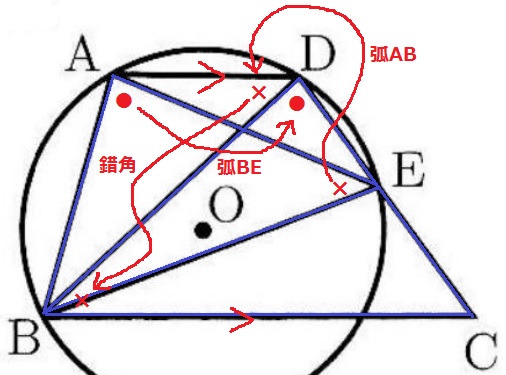
弧ＢＥに対する円周角（●）
弧ＡＢに対する円周角＋ＡＤ//ＢＣの錯角（×）
２角相等で∽
（３）
答案では求める計算も書く。
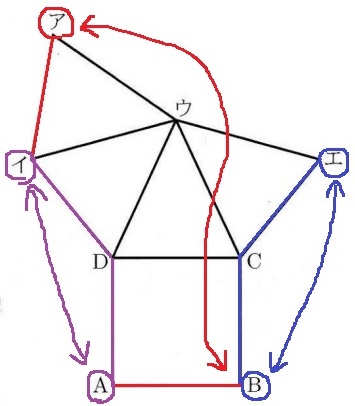
ＤＥ：ＥＣを用いてチョウチョウ型の相似をつくる。
ＡＥとＢＣを延長し、交点をＧとする。
△ＡＤＥ∽△ＧＣＥより、ＣＧ＝①とすると、ＡＤ＝②
仮定（ＢＣ＝２ＡＤ）より、ＢＣ＝④
△ＡＤＦ∽△ＧＢＦより、ＤＦ：ＦＢ＝②：⑤
△ＡＢＤは、４×⑦/②＝14ｃｍ2
台形ＡＢＣＤの上底ＡＤ：下底ＢＣに注目する。
△ＡＢＤ：△ＢＣＤの面積比が①：②だから、
台形ＡＢＣＤの面積は、14×③＝42ｃｍ2
大問１
計算は全問正解したい。
（４）球の体積・表面積の公式も忘れずに！
大問２
（２）おのおのの確率を出して比較する。
記述式なので、どちらかがあっていれば部分点がもらえると思う。
大問３
（３）Ｃのグラフは（10、25）を通過する。分数の傾きをうまく使う。
大問４
プランターの合計数が与えられているので、
植物ではなくプランターの大小をそれぞれ文字に置き換えるとやりやすい。
大問５
条件③が厳しいか。直角二等辺の斜辺の長さを移す。
大問６
（２）体積比＝底面積の比×高さの比。経験の差が出やすい。
（３）△ＢＰＲは不等辺三角形。△ＯＡＢが正三角形→有名角の活用。
大問７
（２）証明は標準レベル。
（３）延長してチョウチョウ。よくある相似形である。
公立高校入試解説ページに戻る
コメント