平均63.6点(前年比;+3.9点)
問題はこちら→岡山県私塾連盟さん
大問1(小問集合)
(1) 99.5%
-1+7
=6
(2) 92.0%
(-8)×(ー2)-(-4)
=16+4
=20
(3) 89.5%
(-3a-5)-(5-3a)
=-3a-5-5+3a
=-10
(4) 85.0%
4a2b÷3/2b
=8/3a2
(5) 83.5%
(√3+2)(√3-5)
=3-5√3+2√3-10
=-7-3√2
(6) 58.0%(部分正答30.0%)
答案では求める過程も記述する。
ある正の整数をxとする。
(x-3)2=64
(x-3)=±8
x=3±8=-5、11
xは正の整数なので、x=11
(7) 82.5%
反比例の比例定数aは積xyで一定。
a=-3×1=-3
y=-3/x
(8) 41.5%(部分正答1.0%)
余事象
(全体1)-(起こる確率p)=(起こらない確率)
1-p
(9) 65.0%(部分正答1.0%)
6の倍数ではない、3の倍数を挙げればいい。
a=3、9、15など。
(10) 12.5%!
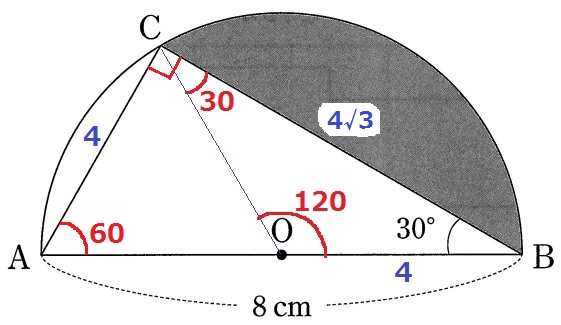
扇形OBCから△OBCをひけば、求積すべき部分が求まる。
COに補助線。
半径より△OBCは二等辺三角形。∠COB=180-30×2=120°
また、半円の弧に対する円周角は90°→∠ACB=90°
△ABCの辺の比は1:2:√3→AC=4cm、CB=4√3cm
AO=OBから、△ABCの半分が△OBCである。
求積すべき部分の面積は、4×4×π×1/3-4×4√3÷2÷2=16/3π-4√3cm2
大問2(データの活用)
(1)① 88.0%
2015年の第3四分位数は8.5秒を下回るが、2010年は8.5秒を超える。〇
ア
② 82.0%
×印などで平均値を示す箱ひげ図もあるが、本問にはそれがないので不明。△
ウ
(2) 70.5%
四分位範囲=第3四分位数-第1四分位数(箱の長さ)
データ全体のうち、真ん中に集まる約50%の散らばり具合を示す。
イ
(3) 64.0%
まず、最大値から9.5~10.0秒の階級がないイは2015年。

全体で何人いるか書かれていない。
ウは全体的にばらついているが、アは7.5~8.5秒に半分以上が集中しており、
四分位範囲が7.5~8.5秒に収まる2020年がアと判断する。
2010年…ウ、2015年…イ、2020年…ア
大問3(方程式)
(1)① 89.0%(部分正答0.5%)

プリンがx個、シュークリームがy個。
180x+120y=1500
② 90.5%
180x+120y=1500 ←÷60
3x+2y=25 …①
個数で等式。
x+y=9 …②
①-②×2で、x=7
②に代入、y=2
プリン…7個、シュークリーム…2個
(2)① 35.5%
不定方程式。
120a+90b=1500 ←÷30
4a+3b=50
aとbは個数だから自然数。
整数解を1つ見つける。a=2のとき、b=14
(a、b)=(2、14)

4×3=3×4
4の個数を+3、3の個数を-4すれば、12が交換されて和が50で一定になる。
(a、b)=(2、14)(5、10)(8、6)(11、2)
4通り
② 54.5%(部分正答2.0%)
先の4通りのなかで、aとbがともに8個以下なのは(8、6)のみ。
シュークリーム…8個、ドーナツ…6個
大問4(関数)
(1)① 80.5%
y=ax2にA(4、4)を代入。
4=16a
a=1/4
② 66.5%
y=1/4x2において、
x=0のとき、最小値y=0
x=4のとき、最大値y=4
0≦y≦4
(2) 39.5%
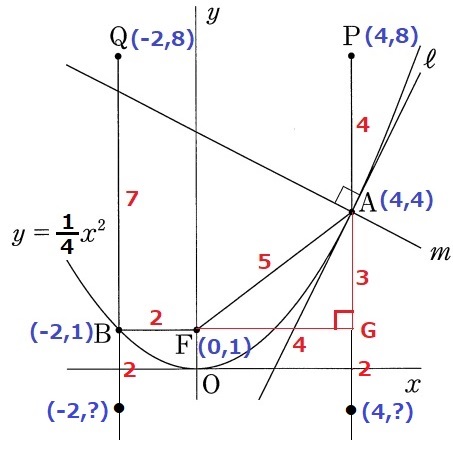
PAとBFを延長した交点をGとする。
AG=4-1=3
FG=4
△AFGは辺の比が3:4:5の直角三角形→AF=5
求めるべき点はAから真下に5離れたところにある。
そのy座標は、4-5=-1
@@
Bでも確認しておく。
y=1/4x2にx=-2を代入して、B(-2、1)
BF=2より、求めるべき点はBから真下に2離れたところ。
y座標は、1-2=-1
@余談@
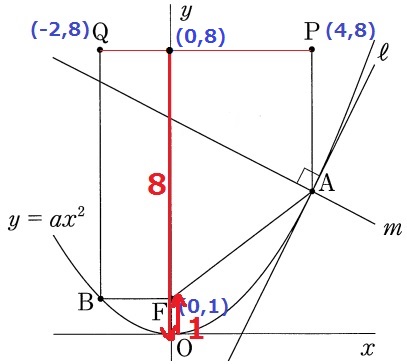
数学から離れますが、軸に平行に入ってきた光や電波が曲面上で反射すると、
同時に焦点Fに到達するので、進んだ距離はどれも等しくなります。
(0、8)からy軸上を通った電波が原点Oで反射して焦点Fにくる距離は8+1=9だから、
PA+AF=QB+BF=9になるはずです。
よって、PとQから真下に9移動した-1が答えになります。
(3) 20.0%!
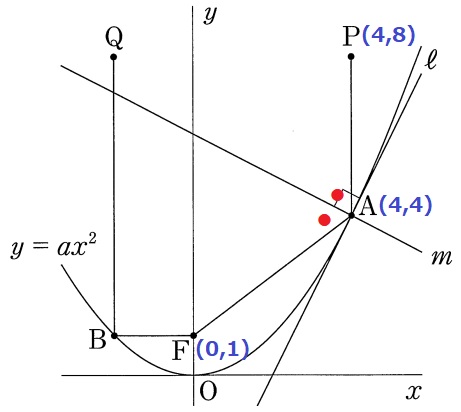
直線ℓ上にはA(4、4)がある。
ℓの傾きを知るには、これと直交するmが手掛かりになるが、
妙な角の二等分線をどう活用すべきか。。
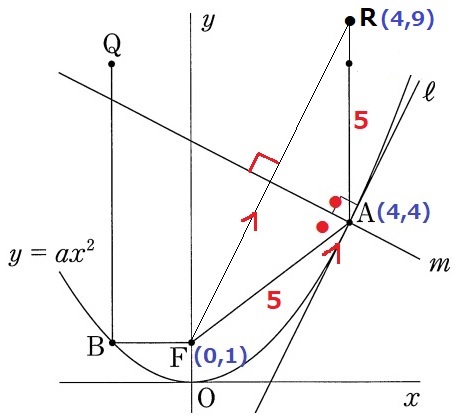
先ほどAF=5とだしたので、AR=5となるR(4、9)を設定する。
△ARFは二等辺三角形で、mは頂角Aの二等分線だから底辺FRを垂直に二等分する。
90°の同位角が等しいので、FRと直線ℓは平行である。
F(0、1)→R(4、9)
右に4、上に8だから、FRの傾きは8/4=2
平行から直線ℓの傾きも2。
RA=5なので切片はFから真下に5移動して、1-5=-4
y=2x-4
大問5(平面図形)
(1)あ…58.5%、い…69.5%
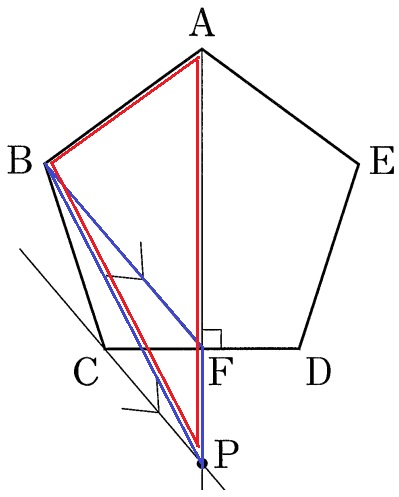
BF//CPで等積変形、△BCF=△BPF
四角形ABCFは△ABPに変形される。
あ…イ、い…オ
(2) 55.0%
Bを通る△ABPを2等分する線分はAPの中点。
ウ
(3)① 26.5%!(部分正答42.0%)
△BCF≡△GFCの証明。
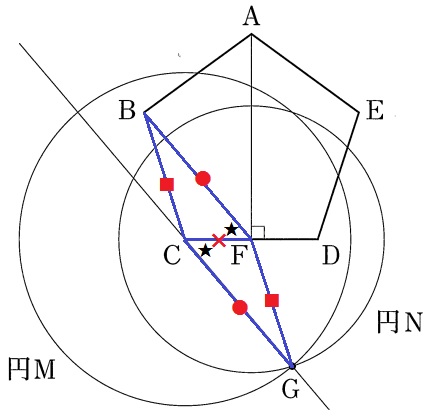
独特な作図であるが、手順からわかることを示せばいい。
円Mの半径はBFと等しいから、BF=GC(●)
円Nの半径はBCと等しいから、BC=GF(■)
共通辺CF=FC(×)
3辺が等しいから合同。
② 84.5%
対応する角から、∠BFC=∠GCF(上図の★)
錯角が等しいので、BF//CGとなる。
ウ
●講評●
大問1
ほぼ基本問題。
(6)正の整数の条件を外さない。
(8)そのまま。難しく考えない。
(10)円の問題がきたら、中心Oと円周上の点を結ぶ。
△AOCは正三角形で、Cから垂線をおろした高さ2√3cmでも△OBCが求まる。
大問2
取りやすい問題が多い。
(3)人数が不明で、ヒストグラムに目盛りがないという変わった設問であった。
(2)で箱の区間は真ん中に集まる約50%のデータが含まれると確認したので、
同様の考えで攻略するのが出題者の意図かと思われる。
もしくは、2010年の第3四分位数が8.5秒を超えており、
8.5秒の人数が多いウと判断した生徒もいたと思う。
大問3
(2)今年度は不定方程式をチラホラ見かけた。
①求め方は複数あるが、中学レベルでは先の解説がやりやすいかなと。
1つの組み合わせがわかれば、4と3の最小公倍数12を交換すれば見つかる。
②前問が正解できればすぐ解ける。点差がつきやすい。
大問4
岡山を特色づけるユニークな設問。
(2)PかQのどちらかがわかれば埋められる。
(3)等角をどう活用すべきか発想力が問われた。
気づければ計算処理はさほどなく、面白い設問である。
大問5
難しくはなかった。
(3)①手順をよく読んで、等辺に印をつけよう。
②∠BFCと∠GCFの関係。選択形式がありがたい。



コメント