2020年度　豊島岡女子学園高校過去問【数学】解説

問題はコチラ→ＰＤＦファイル
50分100点満点

大問１（計算）

（１）
（－２/３ｘ²ｙ）³×３ｘ²ｙ÷（－１/３ｘｙ²）²
＝－８/27ｘ⁶ｙ³×３ｘ²ｙ×９/ｘ²ｙ⁴
＝－８ｘ⁶

（２）

*後ろは有理化ではなく、根号で約分しました。

（３）
ａｘ²－３ａｘｙ－４ａｙ²
＝ａ（ｘ²－３ｘｙ－４ｙ²）
＝ａ（ｘ＋ｙ）（ｘ－４ｙ）

（４）
変化の割合＝（ｙの増加量）/（ｘの増加量）
ｙ＝１/２ｘ²に代入。
ｘ＝１/２のとき、ｙ＝１/８
ｘ＝３のとき、ｙ＝９/２
（９/２－１/８）÷（３－１/２）…①

ｙ＝ ａ/ｘに代入。
ｘ＝１/２のときｙ＝２ａ、ｘ＝３のときｙ＝ａ/３
（ａ/３－２ａ）÷（３－１/２）…②

①と②の値（変化の割合）が等しい。
（９/２－１/８）÷（３－１/２）＝（ａ/３－２ａ）÷（３－１/２）
９/２－１/８＝ａ/３－２ａ
－５/３ａ＝35/８
ａ＝－21/８

大問２（小問集合）

（１）
ｘ²－５ｘ－３＝０に解の公式を適用。
ｘ＝（５±√37）/２
まず、√37の整数部分を考える。
√36＜√37＜√49だから、√37の整数部分は６。
５より√37の方が大きいので、『正の解』は（５＋√37）/２。
（５＋37）/２の整数部分は、（５＋６…）÷２＝11…÷２＝５…
小数部分ａ＝正の解－整数部分＝（５＋√37）/２－５

ａ（ａ＋５）
＝｛（５＋√37）/２－５｝｛（５＋√37）/２－５＋５｝
＝｛（√37－５）/２｝｛（√37＋５）/２｝
＝｛（√37）²－５²｝/４＝12/４＝３

（２）
２ｍ－１≦√ｎ≦２ｍ　←すべて２乗
（２ｍ－１）²≦ｎ≦（２ｍ）²
２ｍ－１と２ｍは連続する整数。
連続する２つの整数の平方数のあいだにある数を考えればいい。
留意すべきは、不等号≦にイコールがあること。
つまり、（２ｍ－１）²もｎに含まれる。
たとえば、４と９の差は９－４＝５個だが、４を含めると５＋１＝６個となる。
ｎ＝2020は（２ｍ－１）²を含む個数なので、（２ｍ）²と（２ｍ－１）²の差は2019。

（２ｍ）²－（２ｍ－１）²＝2019
４ｍ²－４ｍ²＋４ｍ－１＝2019
４ｍ＝2020
ｍ＝505

（３）
７の倍数の判定法は使えにくい(;´Д｀)
地道に代入して調べていくが、余りに注目しよう。
11＝７＋４（余り４）
８＝７＋１（余り１）
余りの合計が７の倍数であれば全体で７の倍数。
たとえば、ａ＝１のとき、
余り４×１＋余り１×３＝７だから、ｂ＝３となる。
ａ＝２のとき、４×２＋１×６＝14→ｂ＝６
ａ＝３のとき、４×３＋１×２＝14→ｂ＝２
ａ＝４のとき、４×４＋１×５＝21→ｂ＝５
ａ＝５のとき、４×５＋１×１＝21→ｂ＝１
ａ＝６のとき、４×６＋１×４＝28→ｂ＝４
以上、６通り→６/36＝１/６

（４）

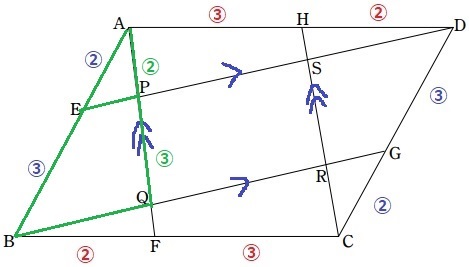
平行四辺形は対辺の長さが等しく、辺を内分する比が同じ。
ＡＦ//ＨＣ、ＥＤ//ＢＧ
△ＡＥＰ∽△ＡＢＱより、ＡＰ：ＰＱ＝ＡＥ：ＥＢ＝２：３

△ＡＤＰ∽△ＨＤＳに注目。
ＨＳ＝②×２/５＝〇４/５
図形全体が点対称なので、対称的に考えてＱＦ＝〇４/５
分数がでてきたので、いったん比を整数に変換。
ＡＰ：ＰＱ：ＱＦ＝②：③：〇４/５＝⑩：⑮：④

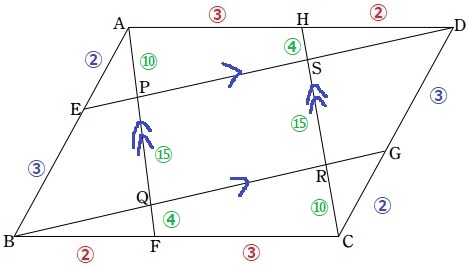
平行四辺形ＡＢＣＤの面積を１として、上底＋下底の和から面積比を計算する。
【平行四辺形ＡＢＣＤ→平行四辺形ＡＦＣＨ→四角形ＰＱＲＳ】
１×６/10×30/58＝９/29
９/29倍

大問３（関数）

（１）
Ｂはｙ＝ｘ²とｙ＝ｘ＋２の交点。
ｘ²＝ｘ＋２
ｘ²－ｘ－２
＝（ｘ＋１）（ｘ－２）＝０
Ｂのｘ座標は正しいだから、Ｂ（２、４）
*Ａの座標は（－１、１）

（２）

ｙ＝１は横線。
Ｂ（２、４）を対称移動させてＣ（２、－２）
②と平行なので傾きは１。
Ｃから切片へ移動。下に２、左に２で（０、４）
ｙ＝ｘ－４

（３）
面積が等しい。等積変形→平行線。
②ｙ＝ｘ＋２から前問のｙ＝ｘ－４との距離が等しく、
②の上側にあるグラフに注目する。

ポイントはｙ軸上で考えること！
ｙ＝ｘ－４の切片は－４
ｙ＝２ｘ＋２の切片は２
距離が６離れるので、Ｐが通る直線の切片は８
ｙ＝ｘ²とｙ＝ｘ＋８の交点座標が答え。
ｘ²＝ｘ＋８
ｘ²－ｘ－８＝０
因数分解ができないので、解の公式。
ｘ＝（１±√33）/２

大問４（方程式）

（１）
表を書いて整理！

豊島岡レベルを狙うならサクッと処理したい。
ｘがｙ％減少→ｘに（１－ｙ/100）倍
40％増→140/100＝７/５倍
2019年の女子は、７/５ｘ（１－ｙ/100）

（２）
ｙしかない男に着目。

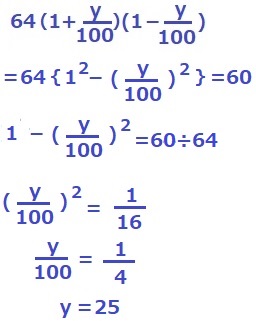
これを、前問の解答に代入。
７/５ｘ（１－25/100）＝63
７/５ｘ×３/４＝63
21/20ｘ＝63
ｘ＝60

大問５（平面図形）

（１）

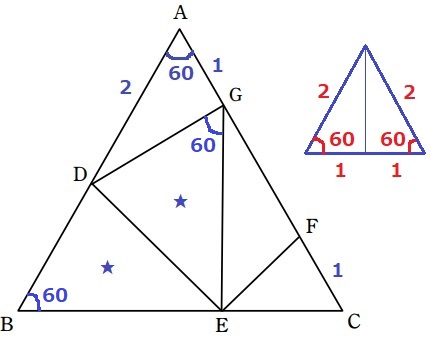
情報の多い△ＡＤＧに着目。
辺の比が２：１で、あいだの角が60°…どこかで見たことのある三角形( ＾ω＾)・・
同じものを２つくっつけると正三角形なので、
△ＡＤＧは１：２：√３の直角三角形→∠ＡＧＤ＝90°

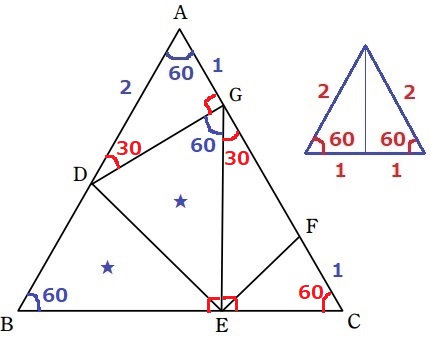
∠ＣＧＥ＝180－90－60＝30°
△ＧＣＥで外角定理→∠ＧＥＢ＝30＋60＝90°
合同より、∠ＤＥＧ＝∠ＤＥＢだから、∠ＤＥＧ＝90÷２＝45°

（２）
△ＡＤＧは１：２：√３の直角三角形→ＤＧ＝√３
合同で、ＤＢ＝√３
正三角形ＡＢＣの１辺ＡＢが２＋√３だから、
ＦＧ＝２＋√３－１－１＝√３

（３）
難問(;´･ω･)
３点を通る円の半径を求めたい場合、まず円の直径を探る。
直径に対する円周角は90°だから、どこかに直角があるはずだが、
△ＥＦＧの内角を調べると∠ＥＦＧ＝90°が導けない…(´ﾟдﾟ｀)
直径はＥＧではないのでは？
そこで、別の直角を探す。

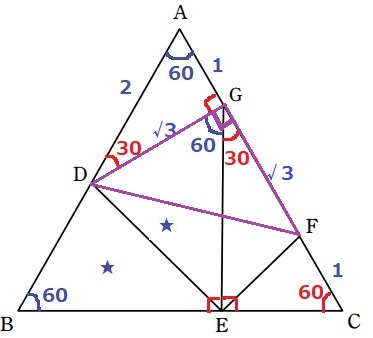
大問３もそうだったが、前問の解答がきちんと誘導になっている。
ＤＧ＝√３、ＧＦ＝√３、∠ＤＧＦ＝90°より、△ＤＧＦは直角二等辺三角形。
∠ＤＧＦを使いたい…。残るＥをどうするか？(‘Д’)

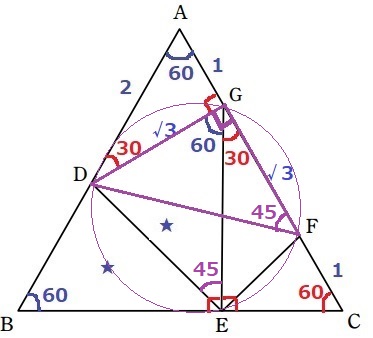
直角二等辺だから、∠ＤＦＧ＝45°
（１）より、∠ＤＥＧ＝45°(‘ω‘ )!!
点Ｅ、Ｆが直線ＤＧにおいて同じ側にあり、∠ＤＥＧ＝∠ＤＦＧが成り立つ。
円周角定理の逆から、４点Ｄ、Ｅ、Ｆ、Ｇは同一円周上にある！
この円の半径を求めればいい。
直径ＤＦは１：１：√２より、√３×√２＝√６
半径は√６÷２＝√６/２

大問６（空間図形）

（１）

小球の中心Ｏは球の半径から面ＡＥＨＤ(左)、面ＡＥＦＢ(前)、面ＥＦＧＨ(底面)から等距離で、
３つの面から等距離にある点の集合は立方体の対角線ＥＣである。
（Ｃも３つの面から等距離にある。ＣＤ＝ＣＢ＝ＣＧ）
ＥＯとＥＰを伸ばすとＣとＧにあたる。
△ＥＯＰ∽△ＡＣＧ
ＥＰ/ＯＰ＝ＥＧ/ＣＧ
ＥＧは正方形の対角線で６√２だから、
ＥＰ/ＯＰ＝６√２/６＝√２

（２）
大球と小球が接するＱは、どの直線上にあるのだろう？(´-`).｡oO

大球の中心をＯ’、Ｑから垂線をおろして足をＲとする。
大球は立方体に接するので、Ｏ’はどの側面の正方形からみても中心。
すなわち、Ｏ’は立方体の中心にあり、立方体の対角線ＥＣ上にある。
小球と大球はＱで接するのでＯ－Ｑ－Ｏ’は一直線、
かつ、ＱはＥＣ上にあるＯとＯ’の間にあるから、ＱもＥＣ上にある。

△ＥＣＧで三平方→ＥＣ＝６√３
△ＥＣＧ∽△ＥＱＲで、ＥＱ：ＱＲ＝ＥＣ：ＣＡ＝６√３：６＝√３：１
 
立方体の中心にあるＯ’は対角線ＥＣの中点。
ＥＯ’＝６√３÷２＝３√３
Ｏ’Ｑは大球の半径３だから、ＥＱ＝３√３－３
ＱＲ＝（３√３－３）×①/〇√３＝３－√３

したがって、四角錘Ｑ－ＥＦＧＨの体積は、
６×６×（３－√３）÷３＝36－12√３

＠データ＠
受験者平均：63.01点
合格者平均：71.81点
やはりボーダーは高いですな|･ω･` )
簡単なところでの失点は痛いです。

豊島岡女子の算数も面白いので、ぜひトライしてみてね(*’ω’*)
とくに大問６の空間がヤバめ。
公立高校入試解説ページに戻る