2023年度　熊本県公立高校入試問題Ｂ過去問【数学】解説

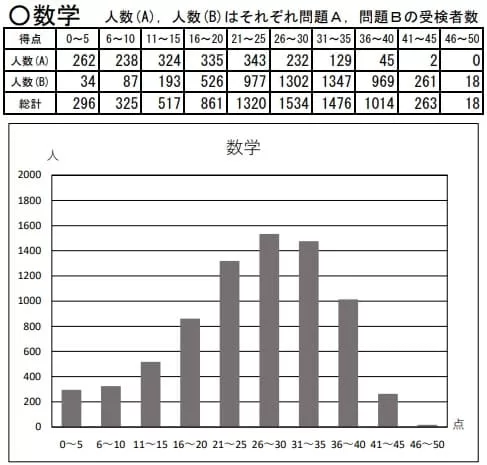
平均28.9点（前年比；＋5.6点）

問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）
１/７＋１/２
＝９/14

（２）
６＋４×（－３）
＝６－12
＝－６

（３）
８ｘ＋９ｙ＋７（ｘ－ｙ）
＝８ｘ＋９ｙ＋７ｘ－７ｙ
＝15ｘ＋２ｙ

（４）
８ａ³ｂ÷（－６ａｂ）²×９ｂ
＝８ａ³ｂ÷36ａ²ｂ²×９ｂ
＝２ａ

（５）
（ｘ＋１）（ｘ－５）＋（ｘ＋２）²
＝ｘ²－４ｘ－５＋ｘ²＋４ｘ＋４
＝２ｘ²－１

（６）
√30÷√５＋√54
＝√６＋３√６
＝４√６

大問２（小問集合）

（１）
５ｘ＋８＝３ｘ－４
２ｘ＝－12
ｘ＝－６

（２）
２ｘ²＋５ｘ－１＝０
解の公式を適用して、ｘ＝（－５±√33）/４

（３）
反比例；ｙ＝ａ/ｘ
比例定数ａは積ｘｙで一定。（ｙ＝ａｘ）
ｙ＝２×３÷５＝６/５

（４）

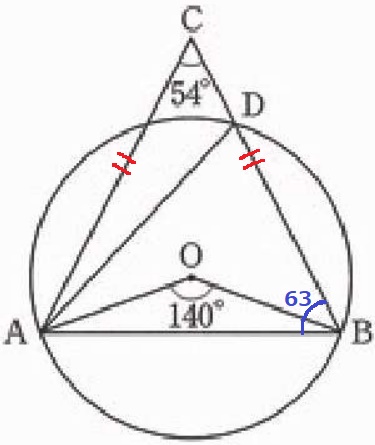
△ＡＢＣは二等辺三角形。
∠ＣＢＡ＝（180－54）÷２＝63°

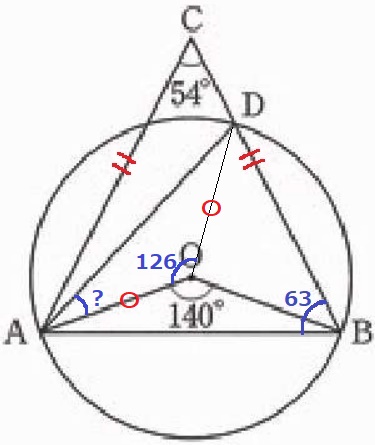
ＯＤに補助線。半径より△ＡＯＤは二等辺である。
弧ＡＤに対する中心角は、63×２＝126°
∠ＯＡＤ＝（180－126）÷２＝27°

（５）

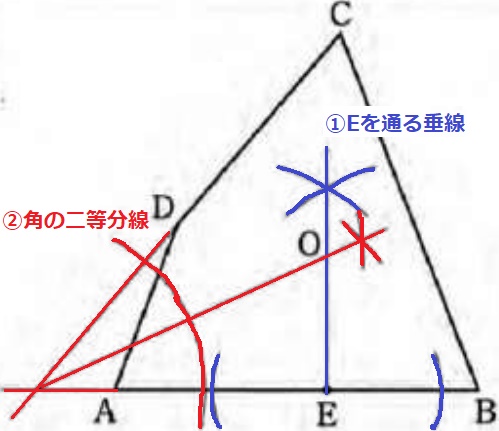
『点Ｅで辺ＡＢに接する』
接点Ｅ、接線ＡＢ→半径と接線は直交する。Ｅを通るＡＢに垂直な線。
『辺ＣＤにも接する』
円の中心はＣＤとＡＢから等距離にある。
ＣＤとＢＡを延長し、２直線がなす角の二等分線。
これらの交点がＯとなる。

（６）①
最大値なので、和より積に絞る。
赤【４】×赤【６】＝24点

②
１個ずつ地道に調べていく。
赤【２】…６、12、５、６、８
赤【４】…12、24、７、８、10
白【２】…５、８、６、８、12
多いのは８点、確率は４/15。
ア…８、イ…４/15

（７）①

航平のグラフを足す。
航平はａ分後に毎分240ｍで出発。
12分後に健太が１周したとき、航平は240ｍ後方にいた。
航平の移動時間は、（2400－240）ｍ÷毎分240ｍ＝2400÷240－240÷240＝10－１＝９分
ａ＝12－９＝３

②

『航平が直樹と最初に並んだ』→航平が直樹を追い越した時間を求める。
直樹の速さは、2400ｍ÷15分＝毎分160ｍ
12分のときに両者は240ｍ離れていた。
１分あたり240－160＝80ｍずつ差が縮まるので、240÷80＝３分後に追いつく。
12＋３＝15分後

③

ｂは直樹を追い越した航平が、ゴールに着くまでに直樹を待つ時間。
仮に航平がそのままゴールした場合、出発から4800÷240＝20分後に着く。
健太の出発から３＋20＝23分後
27－23＝４
ｂ＝４だと航平がゴールに着いてしまい、直樹を待つことができないのでｂ＜４となる。

『航平は直樹を追い越してから２分以上走る』
ということは、ｂの最小値は17分後である。（上図の斜線がｂの範囲）
三角形の∽から、ｂ＝４×２/８＝１
１≦ｂ＜４

大問３（データの活用）

（１）

範囲＝最大値－最小値＝71－43＝28回
四分位範囲＝第３四分位数（Q3）－第１四分位数（Q1）＝60－51＝９回
ア…28、イ…９

（２）
まず、判断しやすい最小値・最大値からチェックする。
１組の最小値は43回→ア・ウ→最大値は71回→ア
２組の最小値は47回→イ・エ

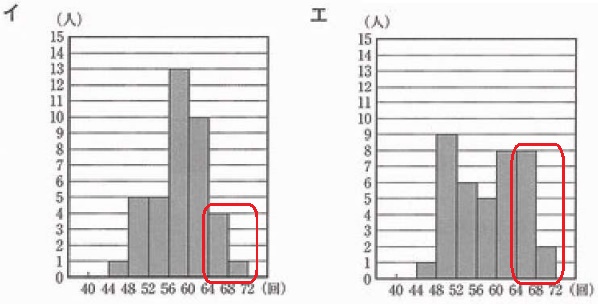
２組のQ3が65回と最大値に近い点に注目する。
39名のQ3は上位19人の真ん中、上から10番目の値。
イは64回以上が５名しかいないので、エが答えとなる。
１組…ア、２組…エ

（３）
ア：範囲＝最大値－最小値。１組の方が大きい。×
イ：四分位範囲＝Q3－Q1。箱の長さで２組の方が大きい。〇
ウ：前問のヒストグラムを見る。64回以上は１組５人、２組10人。〇
エ：平均値を×などで記す箱ひげ図もあるが、本問はわからない。×
イ・ウ

大問４（空間図形）

（１）
三平方の定理から円錐の高さは、√（６²－３²）＝３√３ｃｍ
３×３×π×３√３÷３＝９√３πｃｍ³

（２）
円錐の側面積である扇形の中心角は【360×半径/母線】
円錐の側面積＝母線×母線×π×（360×半径/母線）÷360＝【母線×半径×π】で求められる。
６×３×π＝18πｃｍ³

（３）

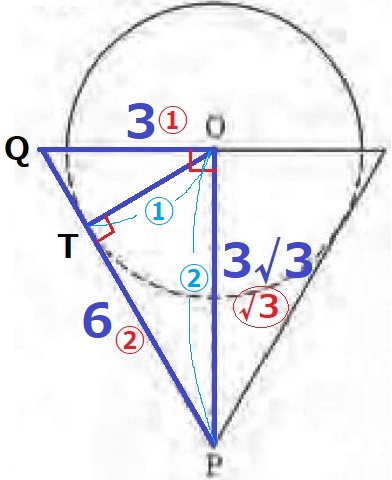
円錐の左端をＱとする。
半径と接線は接点で直交→接線ＰＱとの接点をＴとするとＯＴ⊥ＰＱ
２角相等で△ＯＰＱ∽△ＴＰＯ
△ＯＰＱの辺の比は１：２：√３だから、ＯＰ：ＯＴ＝②：①
球の半径ＯＴ＝３√３×①/②＝３√３/２ｃｍ

（４）

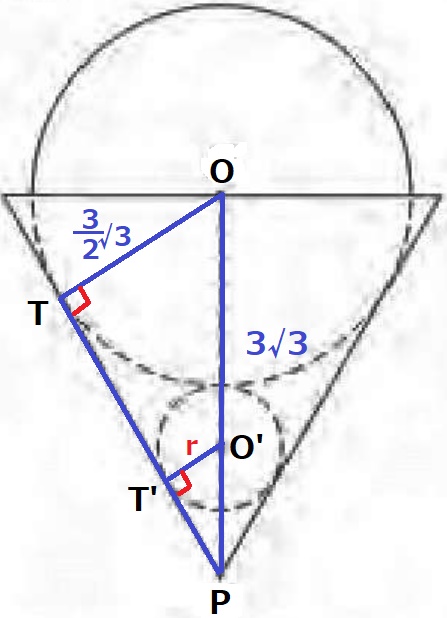
小球の中心をＯ’、ＴＰとの接点とＴ’とする。
Ｏ’Ｔ’⊥ＰＴ
小球の半径ｒ（Ｏ’Ｔ’）が知りたい。

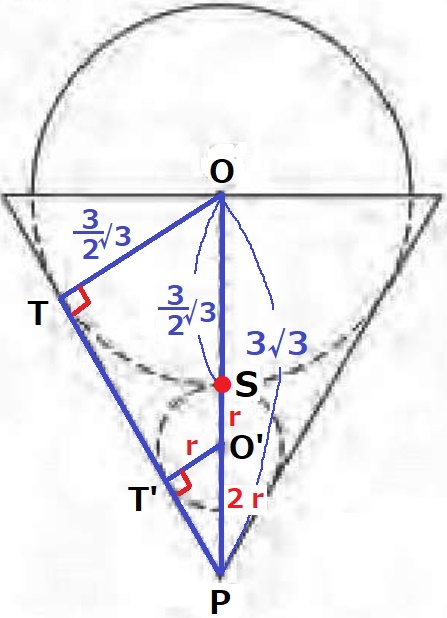
２角相等で、△ＯＴＰ∽△Ｏ’Ｔ’Ｐ
△Ｏ’Ｔ’Ｐの辺の比も１：２：√３である。
大球と小球の接点をＳとすると、半径でＯ’Ｓ＝ｒ
Ｏ’Ｔ’：Ｏ’Ｐ＝１：２より、Ｏ’Ｐ＝２ｒ

半径でＯＳ＝３√３/２だから、ＳＰ＝３√３－３√３/２＝３√３/２＝３ｒ
ｒ＝√３/２ｃｍ
【球の体積Ｖ＝４/３πｒ^３】
４/３π×（√３/２）³＝√３/２πｃｍ³

大問５（関数）

（１）

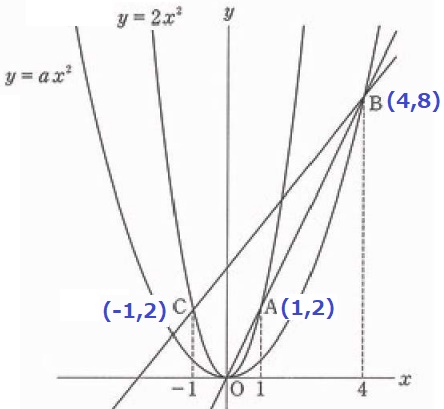
ｙ＝２ｘ²にｘ＝１を代入→Ａ（１、２）
ＯＡの傾きは２、ｙ＝２ｘにｘ＝４を代入→Ｂ（４、８）
ｙ＝ａｘ²にＢ座標を代入。
８＝16ａ
ａ＝１/２

（２）
ｙ＝２ｘ²にｘ＝－１を代入→Ｃ（－１、２）
Ｃ（－１、２）→Ｂ（４、８）
右に５、上に６だから傾きは６/５。
切片はＣから右に１、上に６/５移動して、２＋６/５＝16/５
ｙ＝６/５ｘ＋16/５

（３）①

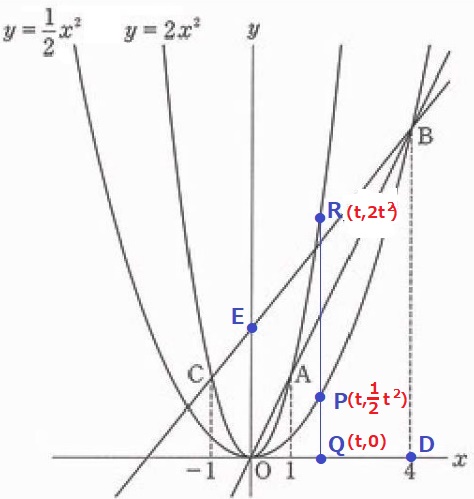
各点を正確に打つ。
求めるべきＰのｘ座標をｔとすると、
Ｐ（ｔ、１/２ｔ²）Ｑ（ｔ、０）Ｒ（ｔ、２ｔ²）

ＰＲ＝ＱＤから方程式を立てる。
２ｔ²－１/２ｔ²＝４－ｔ
３/２ｔ²＋ｔ－４＝０　←２倍
３ｔ²＋２ｔ－８＝（３ｔ－４）（ｔ＋２）＝０
ｔ＞０より、ｔ＝４/３

②

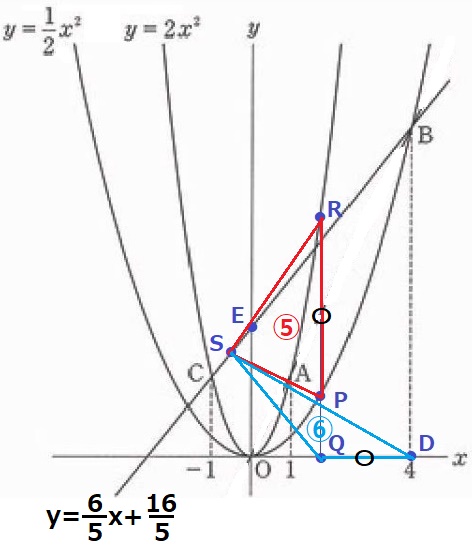
△ＳＰＲの面積を⑤とすると、△ＳＱＤは⑥。
２つの三角形には共通辺がない…。
上図は正確ではないが、ＰＲ＝ＱＤをうまく利用する。

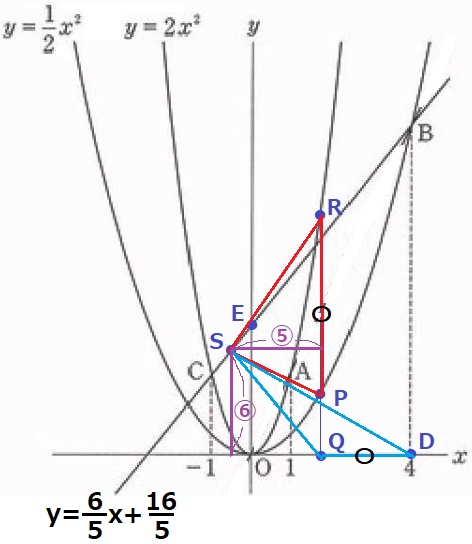
それぞれの三角形の底辺をＰＲ、ＱＤとすると、
底辺が等しい→面積比＝高さの比＝⑤：⑥である。
すなわち、Ｓ～ＲＰの距離：Ｓ～ｘ軸の距離＝⑤：⑥

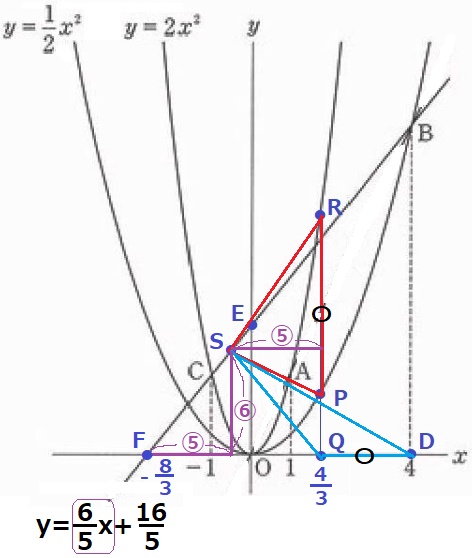
ここで、ＢＣの傾きが６/５であることに着目する。
ＢＣとｘ軸の交点をＦとすると、Ｓから⑥下がり、左に⑤進むとちょうどＦである。
ｘ座標の差をみると、ＳはＦとＱの中点（等距離⑤）にある。

ＢＣの切片は16/５、Ｆは原点Ｏから16/５×５/６＝８/３離れる。
Ｆ（－８/３、０）Ｑ（４/３、０）
Ｓのｘ座標は、（－８/３＋４/３）÷２＝－２/３
ＢＣの式に代入、ｙ＝６/５×（－２/３）＋16/５＝12/５
Ｓ（－２/３、12/５）

大問６（平面図形）

（１）
△ＡＤＦ∽△ＥＣＢの証明。

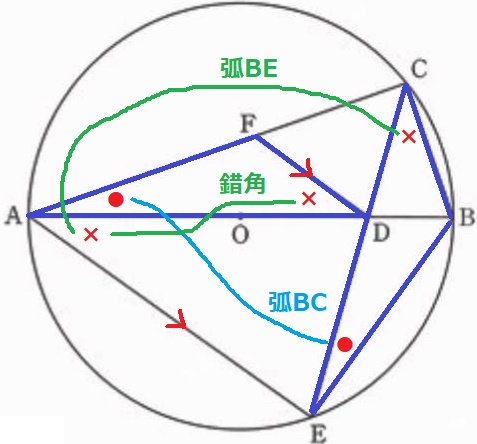
弧ＢＣに対する円周角から、∠ＦＡＤ＝∠ＢＥＣ（●）
ＡＥ//ＦＤの錯角＋弧ＢＥの円周角で、∠ＦＤＡ＝∠ＢＣＥ（×）
２角が等しいので∽

（２）①

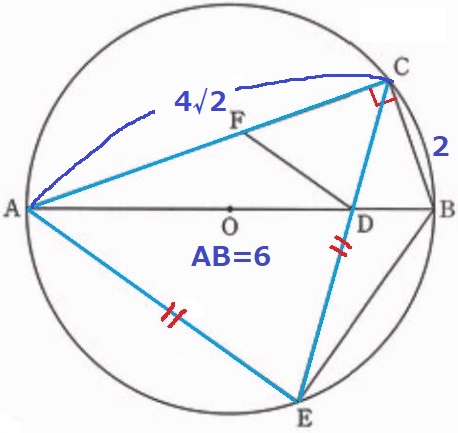
半円の弧に対する円周角より、∠ＡＣＢ＝90°
与えられた長さから、△ＡＢＣで三平方が使える→ＡＣ＝４√２ｃｍ
ここから詰まりやすい…。
ＡＥ＝ＣＥをどう活用するか。△ＡＥＣは二等辺三角形なので…

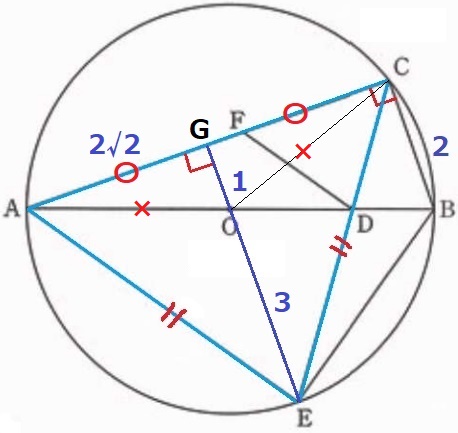
ＥからＡＣに垂線をおろし、足をＧとする。
ＧはＡＣの中点→ＡＧ＝４√２÷２＝２√２ｃｍ
また、この垂線はＡＣの垂直二等分線であり、ＡとＣから等距離にある点の集合である。
半径ＡＯ＝ＣＯから、円の中心Ｏは垂直二等分線上にある。

△ＡＯＧ∽△ＡＢＣより、ＧＯ＝２÷１＝１ｃｍ
半径ＯＥ＝３ｃｍ
△ＡＥＧで三平方→ＡＥ＝２√６ｃｍ

②

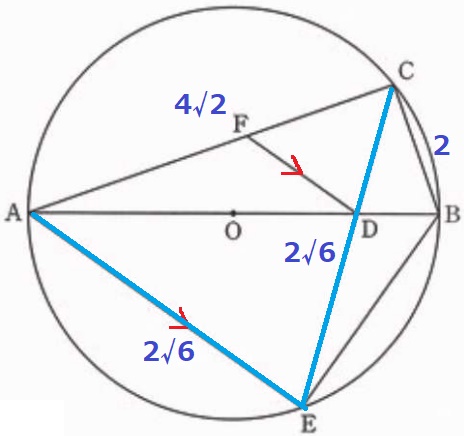
（１）より△ＡＤＦと△ＥＣＢは相似。
相似比がわかれば面積比が求まる。
ＥＣ＝２√６ｃｍなので、これに対応するＡＤが知りたい。
しかし、Ｄの位置がなかなか定まらない(;´Д｀)

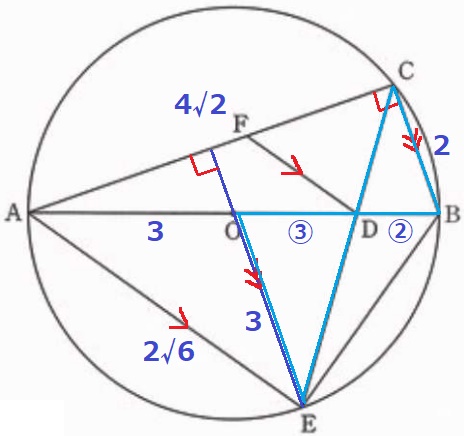
そこで、前問の補助線に目を向けてみる。
∠ＡＧＥ＝∠ＧＣＢで同位角が等しく、ＧＥ//ＣＢ
△ＢＣＤ∽△ＥＯＤより、ＢＤ：ＤＯ＝②：③
半径より、ＡＯ＝ＯＢ＝３ｃｍ
ＯＤ＝３×③/⑤＝９/５ｃｍ
ＡＤ＝３＋９/５＝24/５ｃｍ

相似比は、△ＡＤＦ：△ＥＣＢ＝ＡＤ：ＥＣ
＝24/５：２√６　←×５
＝24：10√６
＝12：５√６
面積比は、△ＡＤＦ：△ＥＣＢ＝12²：（５√６）²＝24：25
△ＡＤＦは△ＥＣＢの24/25倍。

＠別解＠

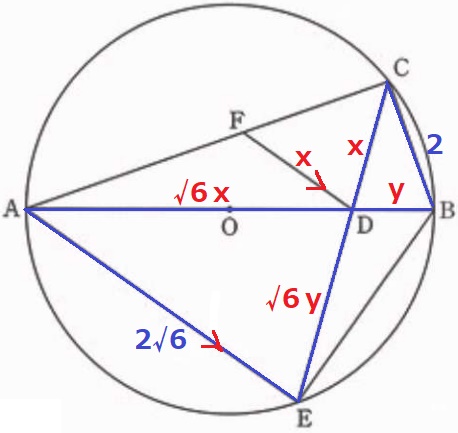
元図だけで攻略するには、根号を含む方程式がでてくるが△ＡＥＤ∽△ＣＢＤを使う。
ＣＤ＝ｘ、ＢＤ＝ｙとすると、ＡＤ＝√６ｘ、ＥＤ＝√６ｙ
また、△ＣＦＤ∽△ＣＡＥから△ＣＦＤも二等辺で、ＦＤ＝ＣＤ＝ｘ
ＡＢ＝√６ｘ＋ｙ＝６　…①
ＣＥ＝ｘ＋√６ｙ＝２√６　…②

①×√６－②をすると、
６ｘ＋√６ｙ＝６√６
－)   ｘ＋√６ｙ＝２√６
５ｘ　　　＝４√６
ｘ＝４√６/５
相似比は、ＦＤ：ＢＣ＝４√６/５：２＝２√６：５
面積比は２乗して24：25となる。