2024年度　宮崎県公立高校入試問題過去問【数学】解説

平均60.4点（前年比；＋8.3点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）－79.0％

（１）　97.2％
－８－（－３）
＝－８＋３
＝－５

（２）　93.2％
－３/７÷（－９/14）
＝２/３

（３）　90.5％
５ｘ＋12＝７ｘ－４
２ｘ＝16
ｘ＝８

（４）　77.3％
２（ａ－２ｂ）－（５ａ－４ｂ）
＝２ａ－４ｂ－５ａ＋４ｂ
＝－３ａ　←ここで代入
＝－３×（－５）
＝15

（５）　78.1％
ｘ²＋４ｘ－12
＝（ｘ＋６）（ｘ－２）＝０
ｘ＝－６、２

（６）　64.1％
３枚のうち、１枚だけ裏になる→３通り
全体は２³＝８通りだから、確率は３/８

（７）　80.6％
標本の選び方→母集団（調査対象の全体）から無作為に抽出する。
ア：県内の中学生のうち、読書活動が盛んな中学生に限定している。×
イ：全国の高校生のうち、ホームページの訪問者に限定している。×
ウ：製造したお菓子のうち。その日の最初に製造したお菓子に限定している。×
エ：製造した電池から無作為に抽出している。〇
エ

（８）　50.2％

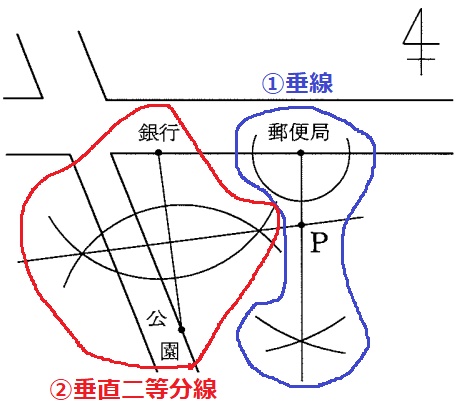
①郵便局の真南→郵便局を通る道路の垂線。
②銀行と公園から等距離→２地点の垂直二等分線。交点がＰ。

大問２（空間図形）－46.3％

（１）　98.0％

正しくないのはウ。

（２）　35.8％

表面積ではなく、側面積を求める。
△ＯＡＢは等辺６ｃｍの二等辺。三平方の定理で高さは４√２ｃｍ。
これが４面あるから、４×４√２÷２×４＝32√２ｃｍ²

（３）　43.3％

Ｏの真下をＨとすると、Ｈは正方形ＡＢＣＤの対角線の交点である。
△ＡＢＣは直角二等辺、ＨはＡＣの中点だから、ＡＨ＝４×√２÷２＝２√２ｃｍ
△ＯＡＨで三平方→ＯＨ＝２√７ｃｍ
正四角錐の体積は、４×４×２√７÷３＝32√７/３ｃｍ³

（４）　18.4％！

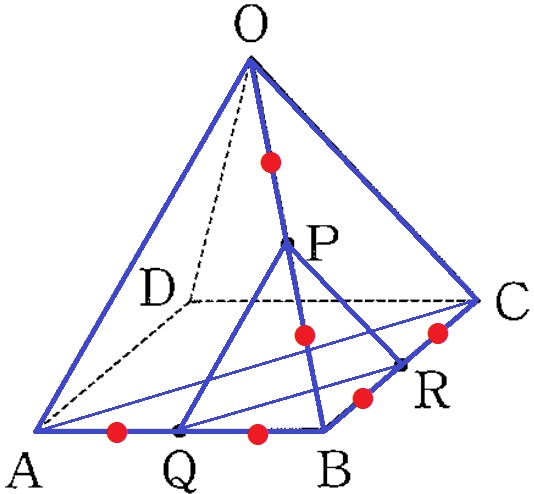
三角錐Ｏ―ＡＢＣ：三角錐Ｐ―ＱＢＲの相似比は２：１→体積比は３乗して⑧：①
三角錐Ｏ―ＡＢＣは正四角錐Ｏ―ＡＢＣＤの半分なので、
三角錐Ｐ―ＱＢＲの体積は、32√７/３÷２×①/⑧＝２√７/３ｃｍ³

大問３（データの活用）－74.7％

（１）①　74.1％

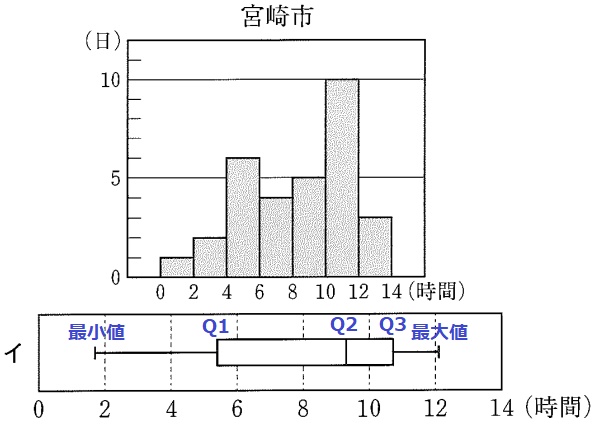
最頻値（モード）は最もあらわれている値。
宮崎市の最頻値は、10～12時間の階級値である11時間。

②　81.9％
31個の中央値は16番目の値。
宮崎市の中央値は８～10時間の階級に含まれる。
ウ

③　74.5％
最大値は12～14時間→ア×
前問より中央値（Q2）は８～10時間→ウ×
イ・エは第１四分位数（Q1）が違う。
31個のQ1は下位15個の真ん中、下から８番目は４～６時間→イ

（２）①　84.9％
四分位範囲＝第３四分位数－第１四分位数
箱が最も短いのは2012年。
（*表から計算すると、28.3－27.4＝0.9）

②　62.4％

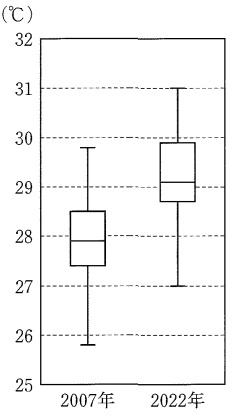
第１四分位数も第３四分位数も2007年より2022年の方が大きいから。

大問４（平面図形）－42.0％

（１）ア…61.7％、イ…54.1％、ウ…29.9％！
∠ＡＣＢ＝∠ＢＡＴの証明。

弧ＡＢに対する円周角より、∠ＡＣＢ＝∠ＡＤＢ（●）
直線ＡＴは接線だから、∠ＤＡＴ＝90°
∠ＢＡＴ＝∠90°－∠ＢＡＤ（×）
また、半円の弧に対する円周角より、∠ＡＢＤ＝90°
△ＡＢＤの内角から、∠ＡＤＢ＝90°－∠ＢＡＤ（×）
よって、∠ＢＡＴ＝∠ＡＤＢ（●）
以上より、∠ＡＣＢ＝∠ＢＡＴ
ア…弧ＡＢ、イ…90°、ウ…90°－∠ＢＡＤ

＠接弦定理＠
『円の接線とその接点を通る弦がつくる角は、その角の内部にある弧に対する円周角に等しい』

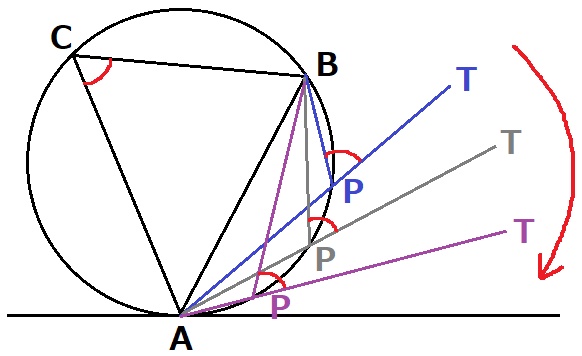
円に内接する四角形の内角はその対角の外角に等しい。
内接する四角形ＡＰＢＣにおいて、弧ＡＢ上でＰを動かしても∠ＡＣＢ＝∠ＢＰＴが常に成り立つ。
ＰをＡに接近させると、接弦定理が成り立つだろうと体感できる。

（２）エ…57.8％、オ…60.0％
△ＣＡＥ∽△ＡＢＥの証明。

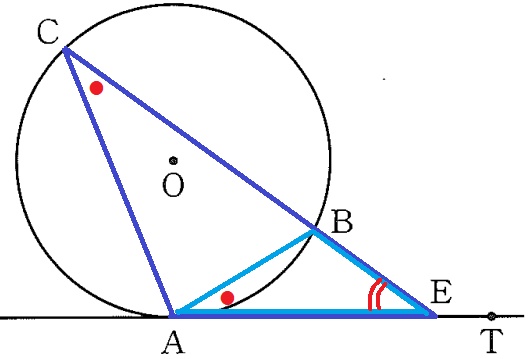
共通角で、∠ＣＥＡ＝∠ＡＥＢ
前の証明より、∠ＡＣＥ＝∠ＢＡＥ
２角が等しいので∽。
エ…∠ＣＥＡ＝∠ＡＥＢ、オ…２角が等しい

（３）①　38.1％

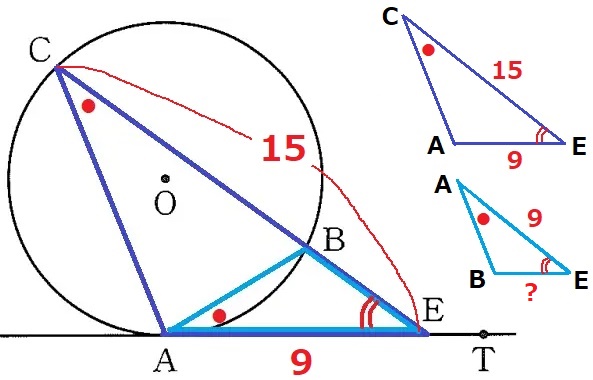
△ＣＡＥ∽△ＡＢＥより、ＢＥ＝９×９/15＝27/５ｃｍ

②　5.8％!!

△ＣＡＥ∽△ＡＢＥの相似比は、15：９＝５：３
面積比は２乗して、△ＣＡＥ：△ＡＢＥ＝㉕：⑨

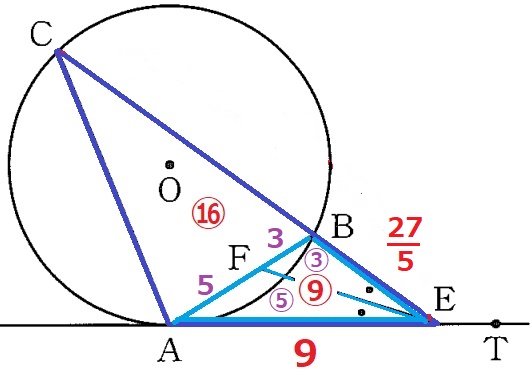
角の二等分線の定理を使います。
ＥＡ：ＥＢ＝ＡＦ：ＦＢ＝９：27/５＝５：３
→△ＡＦＥ：△ＢＦＥ＝⑤：③
△ＢＦＥの面積比を赤の比で示すと、⑨×③/⑧＝〇27/８
△ＢＦＥは△ＣＡＥの〇27/８÷㉕＝27/200倍

大問５（関数）－32.1％

（１）　39.6％
ア：反比例の双曲線は、それぞれ原点について点対称の関係。×
イ：反比例だけ積ｘｙは比例定数ａで一定。×
ウ：いずれも変化の割合は一定ではない。〇
エ：ｙ＝１/２ｘ²（ｘ＜０）はｘが増加するとｙが減少する。×
ウ

（２）　58.7％
ｙ＝１/２ｘ²にｘ＝－２を代入→Ａ（－２、２）
反比例の比例定数ａは積ｘｙなので、
ａ＝－２×２＝－４

（３）①　26.5％！

それぞれの式にｘ座標を代入→Ｂ（２、－２）Ｃ（４、８）
ＡＣの傾きを調べると、Ａから右に６、上に６でＣだから、傾きは６/６＝１

Ｂの真上でＡＣとの交点をＤとする。
Ａから右に４、上に４移動して、Ｄ（２、６）
△ＡＢＣは幅６、高さ８だから、６×８÷２＝24

②　11.9％！
円の中心を特定するには直径を探す。

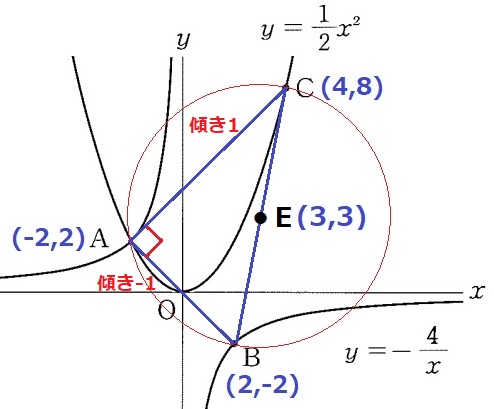
ＡＣの傾きが１→45°
ＡＢの傾きを調べると－１→下に45°
∠ＢＡＣ＝90°
（*直交する２直線の傾きは－１）
半円の弧に対する円周角は90°だから、円の直径はＢＣである。

ＢＣの中点Ｅが円の中心。
Ｂ→Ｃは右に２、上に10だから、Ｅ→Ｃは右に１、上に５。
三平方の定理で半径ＥＣ＝√26
円の面積は、√26×√26×π＝26π