2018年度　茨城県公立高校入試問題過去問【数学】解説

平均51.4点
問題はコチラ→ＰＤＦファイル

大問１（計算）

（１）－９＋４＝－５

（２）（－４）×（－５）＋２×（－３²）　←（－３）²＝９じゃないよ！
＝２０－１８＝２

（３）１/８－（－３/１０）÷６/５
＝１/８＋１/４＝３/８

（４）４（２ｘ－３ｙ）＋３（－ｘ＋４ｙ）
＝８ｘ－１２ｙ－３ｘ＋１２ｙ
＝５ｘ

（５）√４５－５/√５
＝３√５－√５
＝２√５

大問２（計算２）

（１）ｘ²－９ｘ＋８
＝（ｘ－１）（ｘ－８）

（２）連立方程式
５ｘ＋ｙ＝７
２ｘ－ｙ＝７　で連立を組む。

（３）因数分解ができないので解の公式。
ｘの係数が偶数なので、ｂ＝２ｂ’が使える。

（４）不等式
未満だから＝は含まず。

（５）式を整理しよう。
（ｘ＋ｙ）²－（ｘ－ｙ）²
全体をみると・・ａ²－ｂ²＝（ａ＋ｂ）（ａ－ｂ）が使えますね。
（ｘ＋ｙ）²－（ｘ－ｙ）²
＝（ｘ＋ｙ＋ｘ－ｙ）（ｘ＋ｙ－ｘ＋ｙ）
＝２ｘ・２ｙ＝４ｘｙ＝４√６
計２０点。大問１とあわせて４０点ももらえる。

大問３（小問集合）

（１）角度
△ＡＢＥの内角から、∠ＥＡＢ＝１８０－（７８＋４２）＝６０°
弧ＢＤ：弧ＤＥ＝２：１なので、∠ＢＡＤ：∠ＥＡＤ＝２：1
∠ＢＡＤ＝６０×２/３＝４０°

（２）一次方程式
昨日のショートケーキ１個の値段をｘ円とおく。
昨日の売り上げ：２００ｘ
今日の売り上げ：（ｘ－３０）×200×120/100
以上から方程式を組む。
２００ｘ＋５４００＝（ｘ－３０）×２００×120/100
これを解いて、ｘ＝３１５　→　３１５円

（３）確率
√ａｂが自然数になる→ａｂの積が平方数
ａｂ＝１、４、９、１６、２５、３６（サイコロの目は６までなので、６×６＝36まで）
組み合わせは（１、１）（１、４）（４、１）（２、２）（３、３）（４、４）（５、５）（６、６）の８通り。
全体は６×６＝３６通りなので、８/３６＝２/９

大問４（関数）

（１）
Ａ座標は（２、４）
これを、ｙ＝ａ/ｘに放り込み。
４＝ａ/２　　ａ＝８

（２）
∠ＢＰＣ＝２∠ＢＯＣと、奇妙な角度の関係性が与えられている。
とりあえず、∠ＢＰＣ＝②、∠ＢＯＣ＝①と書いておく。
△ＯＰＣに注目！

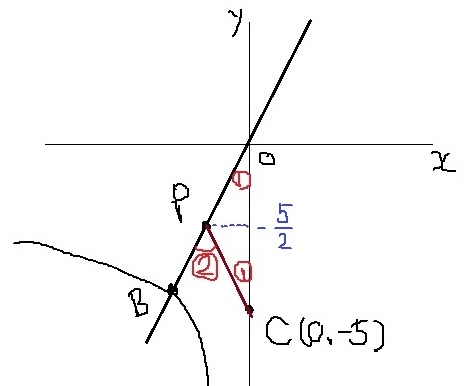
↑△ＯＰＣの外角定理から、∠ＰＣＯも①となる。
底角が等しいから、△ＯＰＣは二等辺三角形。
Ｐからｘ軸に平行な横線をひくと、ｙ軸との交点はＯＣの中点となる。
（二等辺三角形の頂角を通り、底辺に垂直な線分は底辺を２等分するため）
Ｃ（０、－５）なので、ＯＣの中点座標は（０、－５/２）
Ｐのｙ座標も－５/２。
ＢＯ：ｙ＝２ｘだから、これに代入すると、
Ｐ（－５/４、－５/２）

大問５（平面図形）

（１）合同図形の証明
等角を書き入れる。
各々の三角形は１辺と両端角で等しい。
詳しくは、公式解答を参照。

（２）ＨＧ//ＢＣなので、問題文の図と異なる。
空きスペースに書いてみる。

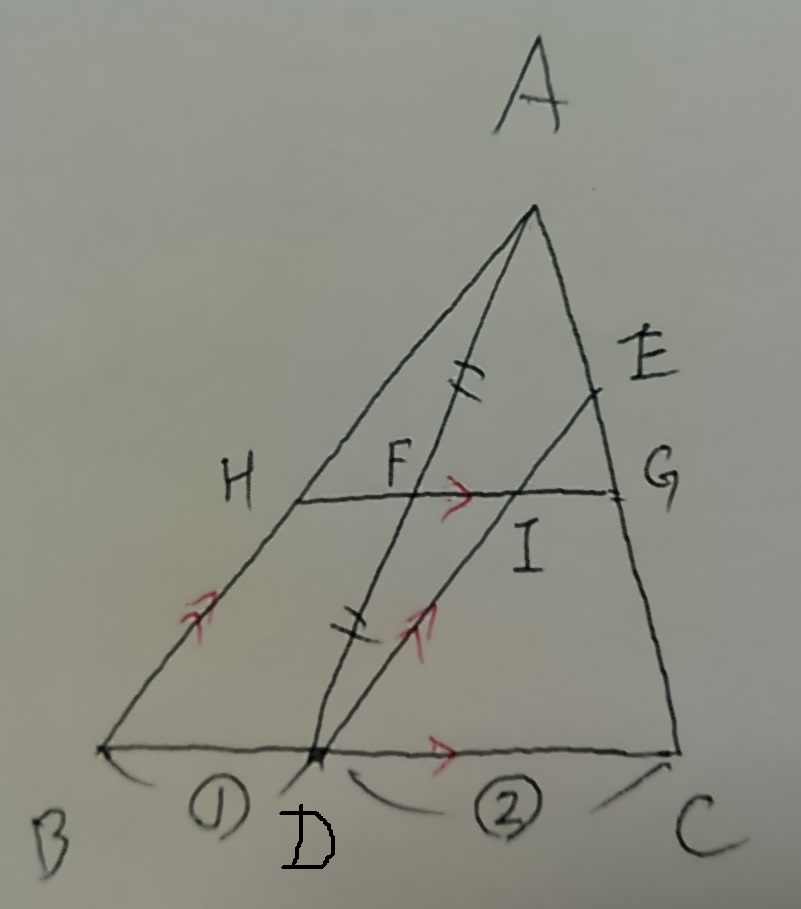
↑問題文の情報を漏れなく記載
ＢＤ：ＤＣ＝１：２から、ＡＥ：ＥＣ＝１：２
ＡＦ：ＦＤ＝１：１から、ＡＧ：ＧＣ＝１：１

すると、△２＝③となるので、共通の比になおす。

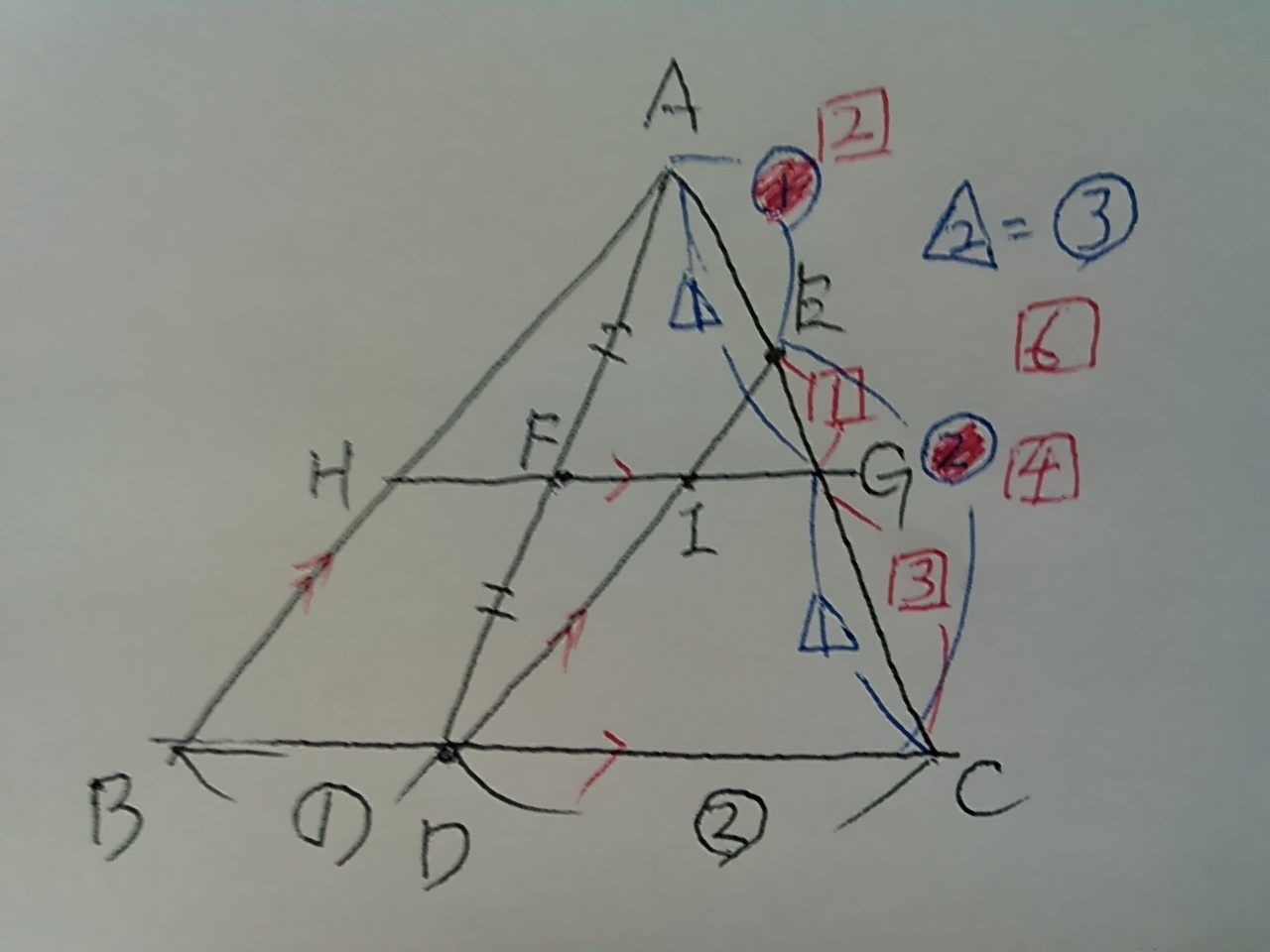
ＡＥ：ＥＧ：ＧＣ＝２：１：３となる。
材料がそろったので計算。
△ＡＢＣ全体を１とおくと、
△ＥＤＣ＝1 ×（②×②）/（③×③）＝４/９
△ＥＤＣ内で、△ＥＩＧは（□１×□１）/（□４×□４）＝１/１６
四角形ＩＤＣＧは、△ＥＤＣの１５/１６だから、
４/９×１５/１６＝５/１２　　→　５/１２倍

大問６（数量変化）

（１）Ａ市の１０～２０ｍ³までは、１ｍ³ あたり１５０円↑
この間のグラフの式を求めておく。
傾きは１５０。
切片はｙ＝ａｘ＋ｂにあてはめてもよいが、
グラフを延長するとｙ軸で－５００のところにぶつかる（左に２いくと下に３下がる）。
よって、ｙ＝１５０ｘ－５００
ｘ＝１７を代入。
ｙ＝１５０×１７－５００＝２０５０円

（２）Ｂ市もグラフに表してみる。

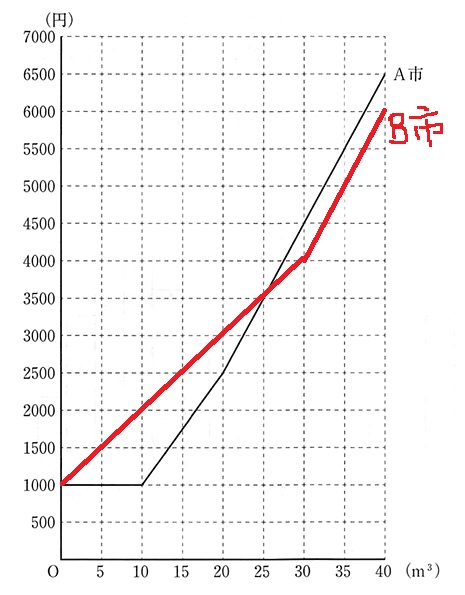
あとは表3にあわせて、Ａ市とＢ市の合計の差を算出。
かなり面倒くさそうにみえるが、よ～く表とグラフをみてみよう。
表の使用量は、６月を除いて２０～３０ｍ³の範囲内。
この範囲はＡ市とＢ市でグラフの傾きが変わらない。
そして、２５ｍ³でＡ市とＢ市の水道料金が等しくなる。
これを念頭に表を見てみよう。
　
１月は２５ｍ³なので、Ａ市とＢ市での差は±０。
２月と３月を一体して考えると、２０は２５から－５で、３０は２５から＋５だから、
２・３月をあわせたＡ・Ｂの合計の差はゼロ。
同様に、４・５月は２８と２２の平均が２５だから、こちらも±０.。
６月は３２ｍ³で、３０ｍ³以降はＡ市とＢ市の傾きが２００で平行となり、差はどこも５００。
よって、１～６月の合計を比べた場合、Ｂ市の方が５００円安くなる。
　
全部の値をいちいち求めていたら時間がつぶれ、ケアレスも発生しやすい。
求める答えはＡとＢの合計の差。
２５で両者が同じ。
そこからの差の平均がプラマイゼロの組み合わせを選んで相殺すれば、
ショートカットできますね。

大問７（データの活用）

（１）統計の基礎
ア：階級の幅はいずれも５。
イ：モードは一番数が多いところ。
ウ：40-45ｍがいる、２年１組。
エ：１５ｍ未満はどちらも５人だが、１組は２９名に対して２組が３１名。
分母が異なるので割合も異なる。

（２）メジアン（中央値）の処理
３１名の真ん中の値は、（３１＋１）÷２＝１６人目
欠席者は16ｍと19ｍなので、図１の１５～２０に２つ追加。
下から順に数えていくと、１６人目は２０～２５の階級にあたる。
５÷３１＝０．１６１・・　→　０．１６

大問８（空間図形）

（１）△ＯＡＢは１辺が８ｃｍの正三角形。その高さは４√３。
よって、８×８＋８×４√３×１/２×４＝６４＋６４√３ｃｍ³

（２）どこで三平方をとるか。
ＡＣとＤＢの交点、つまり、底面積である正方形のどまんなかをＨとおく。
このとき、∠ＥＨＦは直角になる。
なぜなら、正方形の対角線は垂直に交わり、
二等辺三角形ＯＤＢは線分ＡＣと垂直に交わるから、
面ＯＤＢ上にある辺ＥＨも線分ＡＣに対して垂直に交わる。
△ＥＦＨで三平方。

ＥＨの長さも△ＯＤＢで考えよう。
中点連結定理から、すぐ４ｃｍとでる。
△ＥＦＨで三平方の定理。
ＥＦ＝√（４²＋３√２²）
＝√３４ｃｍ
公立高校入試解説ページに戻る