問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）①
－４＋７
＝３
②
６＋７/９×（－12）
＝６－28/３
＝－10/３
③
－２（ａ－ｂ）＋５（２ａ－ｂ）
＝－２ａ＋２ｂ＋10ａ－５ｂ
＝８ａ－３ｂ
④
√28－√７＋√63
＝２√７－√７＋３√７
＝４√７
⑤
（ａ＋５）2－（ａ－８）（ａ－２）
＝ａ2＋10ａ＋25－ａ2＋10ａ－16
＝20ａ＋９
（２）
（ｘ＋２）2＝√13
ｘ＋２＝±√13
ｘ＝－２±√13
（３）
√（126ｎ）＝３√（14ｎ）
ｎ＝14
＠余談＠
２番目に小さいｎ…14×２2＝56
３番目に小さいｎ…14×３2＝126
（４）
反比例はｘとｙの積が比例定数ａで一定。
ａ＝２×（－３）＝－６
ｙ＝－６/ｘ
（５）①
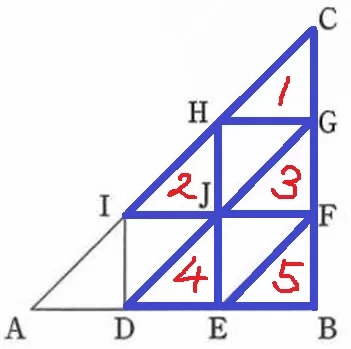
平行移動だけなので、△ＡＤＩは傾けない。
５個
②
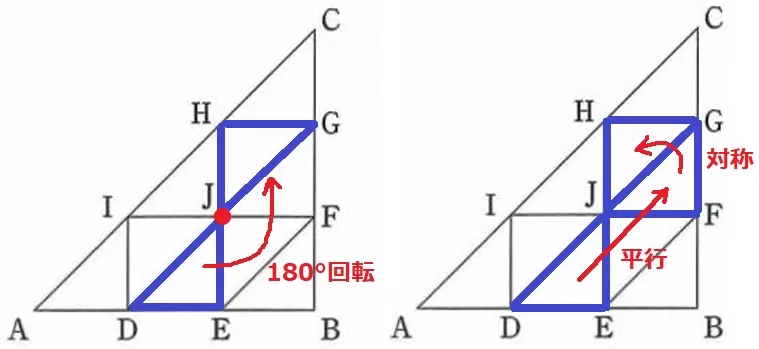
△ＤＥＪを△ＧＨＪに移す。
●方法１
Ｊを中心に180°回転移動（点対称移動）
●方法２
△ＪＦＧへ平行移動→ＧＪを対称の軸として対称移動。
ア…180、イ…ＧＪ
（６）
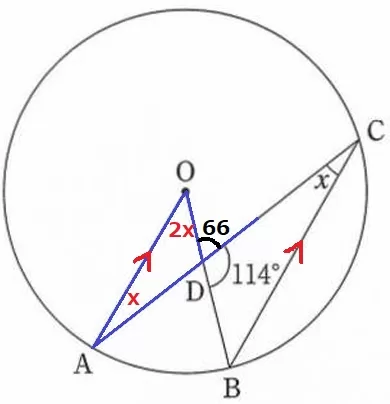
∠ＯＤＣ＝180－114＝66°
ＯＡ//ＣＢの錯角から、∠ＯＡＣ＝ｘ
中心角は円周角の２倍→∠ＡＯＢ＝∠ＡＣＢ×２＝２ｘ
△ＡＯＤで外角定理、ｘ＋２ｘ＝３ｘ＝66
ｘ＝22°
大問２（小問集合２）
（１）
Ａ→Ｂ：底辺ＡＤは一定、高さＡＰだけが増加→△ＡＰＤの面積は比例で増加。
Ｂ→Ｃ：底辺ＡＤ、高さＡＢが一定→等積変形で面積も一定。
ア
（２）
答案では求める過程も記述する。
一般道路をｘｋｍ、高速道路をｙｋｍとする。
距離で等式。
ｘ＋ｙ＝130 …①
時間で等式。２時間のドライブなので、
ｘ/30＋ｙ/80＝２ ←240倍
８ｘ＋３ｙ＝480 …②
②－①×３をすると、５ｘ＝90
ｘ＝18
①に代入、ｙ＝130－18＝112
一般道路…18ｋｍ、高速道路…112ｋｍ
（３）
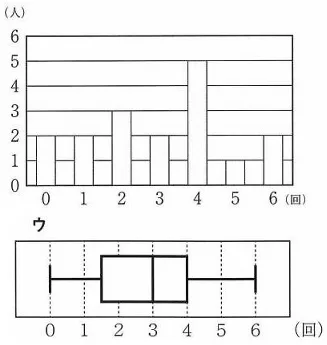
最大値は６回（エ×）
17人の中央値は９番目の値で３回（イ×）
残りのア・ウで異なるのは第３四分位数。
上位８人の真ん中、上から４番目と５番目の平均で４回（ア×）
ウ
（４）
計算式のＢで場合分け。
●６＋ａ
６は偶数。偶数＋奇数＝奇数だからａは奇数である。３通り
●６－ａ
偶数－奇数＝奇数だから、ａは６未満の奇数。３通り
●６×ａ
積が奇数となるのは、奇数×奇数＝奇数しかない。
偶数６をかける時点で０通り。
計６通り。全体は５×３＝15通りなので、確率は６/15＝２/５
（５）①
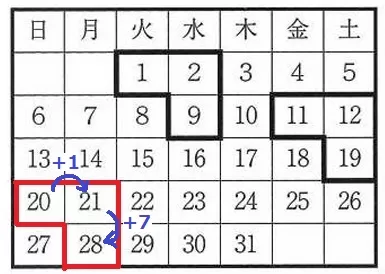
右上の数字が奇数であればどこでもいい。
20＋21＋28＝69
②
最も小さい数をｎとすると、他２つはｎ＋１、ｎ＋８。
ｎ＋（ｎ＋１）＋（ｎ＋８）
＝３ｎ＋９
＝３（ｎ＋３）
ｎ＋３は整数だから、３（ｎ＋３）は３の倍数である。
よって、３つの数の和はいつも３の倍数になる。
大問３（関数）
（１）
ｙ＝２ｘ2について、
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－２のとき、最大値ｙ＝８
０≦ｙ≦８
（２）
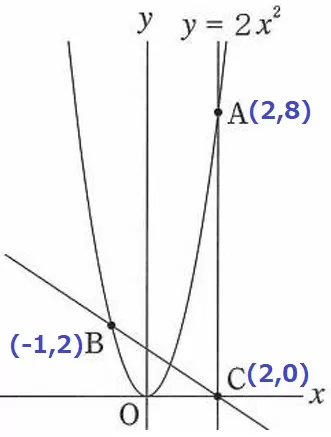
Ｂ（－１、２）→Ｃ（２、０）
右に３、下に２だから傾きは－２/３。
Ｃから左に２、上に２×２/３＝４/３移動して、切片は４/３。
ｙ＝－２/３ｘ＋４/３
（３）
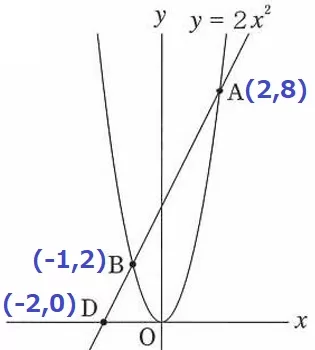
Ｂ（－１、２）→Ａ（２、８）
右に３、上に６だから、傾きは６/３＝２
Ｂから下に２、左に１移動して、Ｄ（－２、０）
ｘ座標の差から、ＡＢ：ＢＤ＝３：１
（４）
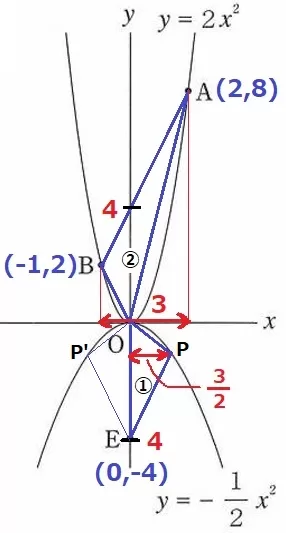
ＡＢ；ｙ＝２ｘ＋４
△ＯＡＢは切片４、幅が３。
△ＯＰＥの面積は△ＯＡＢの半分、ＯＥ＝４だから、
幅（ｙ軸とＰのｘ座標との距離）が３÷２＝３/２になればいい。
Ｐのｘ座標は３/２。
これをｙ＝－１/２ｘ2に代入して、（３/２、－９/８）
もう１つは、これをｙ軸について対称移動させた（－３/２、－９/８）
（３/２、－９/８）（－３/２、－９/８）
大問４（平面図形）
（１）
△ＢＨＧで三平方→ＢＨ＝√29ｃｍ
（２）
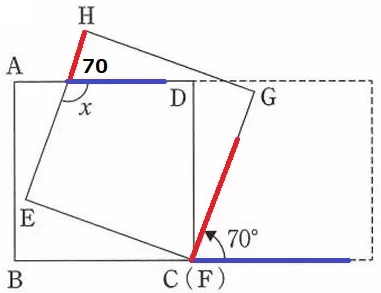
青線同士と赤線同士が平行。
青線と赤線がなす角は70°
ｘ＝180－70＝110
（３）①
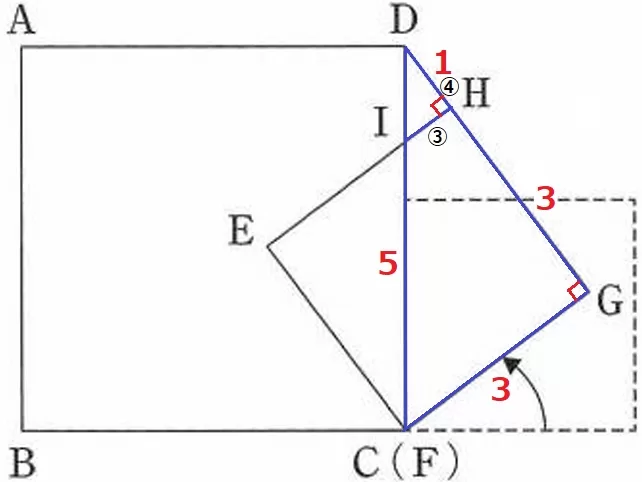
正方形の１辺からＤＣ＝５ｃｍ、ＣＧ＝３ｃｍ
→△ＤＣＧは３：４：５の直角三角形なので、ＤＧ＝４ｃｍ
△ＤＩＨ∽△ＤＣＧより、△ＤＩＨの辺の比も３：４：５。
ＤＨ＝４－３＝１ｃｍ
ＩＨ＝１×③/④＝３/４ｃｍ
△ＤＩＨの面積は、１×３/４÷２＝３/８ｃｍ2
②
３点Ｂ・Ｅ・Ｈが一直線上に並ぶことを証明する。
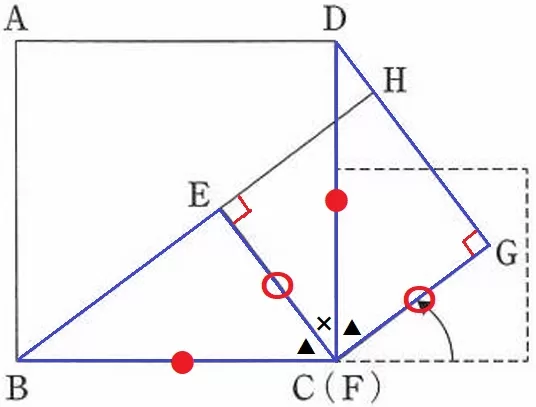
∠ＣＥＨ＝90°だから、∠ＢＥＣ＝90°であればＢＨは一直線である。
∠ＢＥＣを内角とする△ＢＣＥに着目する。
△ＢＣＥ≡△ＤＣＧであれば、対応する角から∠ＢＥＣ＝∠ＤＧＣ＝90°が導ける。
仮定（正方形の１辺）よりＢＣ＝ＤＣ、ＣＥ＝ＣＧ
∠ＢＣＥ＝90－∠ＥＣＤ、∠ＤＣＧ＝90－∠ＥＣＤ→∠ＢＣＥ＝∠ＤＣＧ
２辺と間の角が等しいから△ＢＣＥ≡△ＤＣＧ
∠ＢＥＣ＝∠ＤＧＣ＝90°で、∠ＢＥＣ＋∠ＣＥＨ＝90＋90＝180°
したがって、３点Ｂ、Ｅ、Ｈは一直線上に並ぶ。
大問１
（２）カッコは展開しない。
（３）√126をａ√ｂに変形。ｂをかければ根号が外れる。
（５）図形の平行・回転・対称移動。2024北海道（大問５）でも出題。
大問２
全体的に点が取りやすい。
（４）特殊な設定っぽいが、偶奇判定でわりとスッキリ求められる。
（５）②３の倍数である→３でくくれる。
大問３
（３）までは正解したい。
（４）ＯＥがｙ軸上の線分でＥ（０、－４）がありがたい。
高さが４で共通なので、幅が半分であれば面積が半分。
Ｐのｘ座標が正か負で２通りある。
大問４
（２）２組の平行線の技は覚えておくと得。
（３）△ＤＩＨと∽にある三角形を見つけやすい。
△ＣＩＥとの相似からでもＩＨを出せる。
（３）最初に方針をきちんと立てられるか。
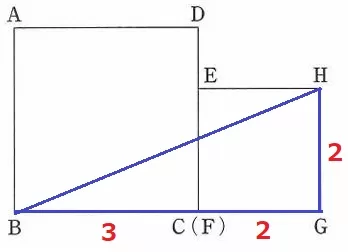
一直線→180°→∠ＣＥＨ＝90°だから、∠ＢＥＣ＝90°がわかればいい。
これを内角とする△ＢＣＥと相似か合同にあたる三角形で、
∠ＢＥＣに対応する角が90°の三角形はないか。構図がシンプルなので見つけやすい。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント