*かなりの高難易度です。
問題PDF
大問1(計算)
(ア)
7-(-12)
=7+12
=19 【4】
(イ)
-2/7+3/5
=11/35 【3】
(ウ)
54a2b×3b÷9ab
=18ab 【3】
(エ)
(3x-y)/2-(2x+4y)/3
={3(3x-y)-2(2x+4y)}/6
=(9x-3y-4x-8y)/6
=(5x-11y)/6 【1】
(オ)
(3+√5)(3-√5)-6(1-√5)
=9-5-6+6√5
=-2+6√5 【2】
大問2(小問集合)
(ア)
(x-3)2-4(x-3)-32 ←X=x-3とおく
=X2-4X-32
=(X-8)(X+4) ←X=x-3を戻す
=(x-3-8)(x-3+4)
=(x-11)(x+1) 【1】
(イ)
4x2+6x+1=0
解の公式を適用。xの係数が偶数なのでb=2b’が使える。
x=(-3±√5)/4 【1】
(ウ)
y=ax2において、xの値が2→4に増加するときの変化の割合はa(p+q)
a(2+4)=4
a=2/3 【4】
(エ)
小さい正方形の1辺をxとすると、大きい正方形の1辺はx+9。
x2+(x+9)2
=2x2+18x+81=305
2x2+18-224=0 ←÷2
x2+9x-112
=(x-7)(x+16)=0
x>0より、x=7 【3】
(オ)
扇形の中心角が知りたい。
半径9cmの円周は18πcm。
弧の長さが2πcmなので、扇形は2π/18π=1/9円である。
扇形の面積は、9×9×π×1/9=9πcm2 【2】
@余談@
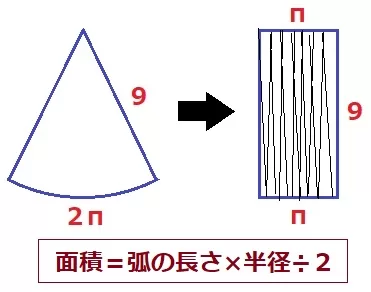
扇形の面積は、弧の長さ×半径÷2で求めることができる。
とある界隈ではスーパー三角形というそうな( ´д)ヒソ(´д`)ヒソ(д` )
理屈は円の面積の公式と同じで、扇形を細かくスライスして互い違いに並べると、
縦が半径、横が弧の半分の長さである長方形になるから。
(カ)
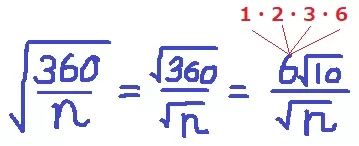
6√10/√nが整数となるには、n=10で√10を約分する。
また、√nが6の約数を含む場合も分母を消せる。
ということは、n=10×(6の約数の平方数)となる。
6の約数は4個なので、nは4個。
(*具体的にいうと、n=10×12=10、10×22=40、10×32=90、10×62=360の4個)
大問3(小問集合2)
(ア)ⅰ
△ABF∽△BCEの証明。
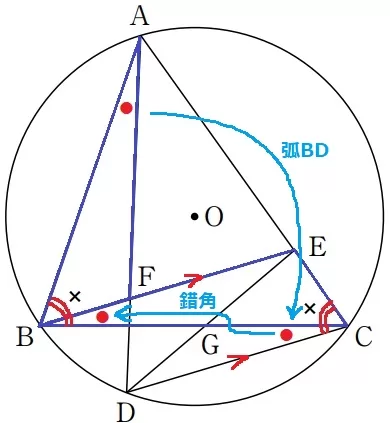
弧BDに対する円周角より、∠BAD=∠BCD(●)
DC//BEの錯角で、∠BCD=∠CBE(●)
よって、∠BAF=∠CBE
仮定より、∠ABC=∠ACD
∠ABE=∠ABC-∠CBE(●)
∠ACB=∠ACD-∠BCD(●)
よって、∠ABF=∠BCE(×)
2角が等しいので∽。
a…【3】、b…【4】
ⅱ
もう難問が。。
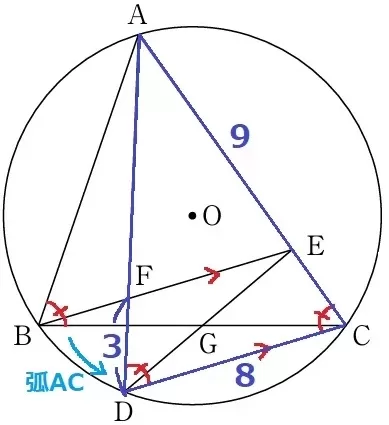
弧ACに対する円周角で∠ABCを移すと、
∠ADC=∠ACDとなり、△ADCは二等辺三角形。
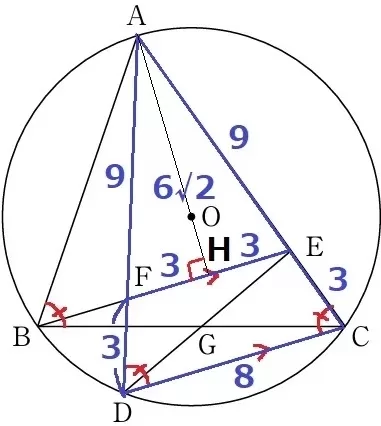
FE//DCと二等辺の対称性から、
AF=AE=9cm、FD=EC=3cm
△AFE∽△ADCより、FE=8×9/12=6cm
最終的に△CEGの面積を求めたい。
面積を出すには高さが必要なので、二等辺AFEを二等分するAHをつくり、
△AFHで三平方→AH=6√2cmと求めておく。
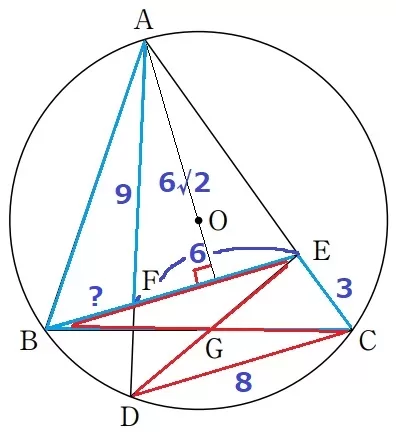
いったん、方針を立てる。
△EGCの求積にはGの位置を特定しなければならない。
Gに関わる相似は△BEG∽△CDG。
CDに対応するBEの長さを知るにはBFが必要。
また、BFがわかれば△ABFの面積が求まり、前問より相似である△BCEの面積もでるはず。
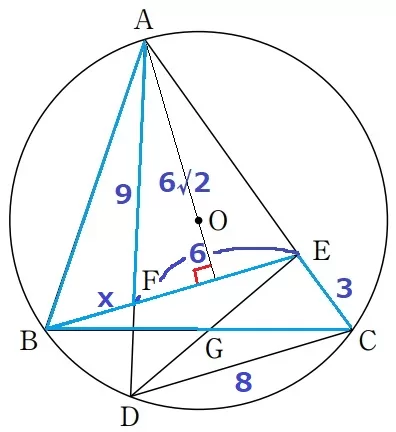
そこで、BFに狙いを絞ってこれをxとする。
△ABF∽△BCEより、AF:BF=BE:CE
9:x=(x+6):3
内項と外項の積より、x(x+6)=27
x2+6x-27
=(x+9)(x-3)=0
x>0より、x=3
BF=3cmということは、△ABF≡△BCEである。
△ABF=△BCE=3×6√2÷2=9√2cm2
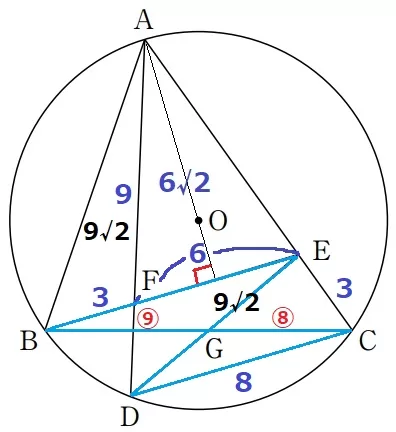
△BEG∽△CDGより、BG:GC=⑨:⑧
△CEGの面積は、9√2×⑧/⑰=72√2/17cm2
(イ)ⅰ
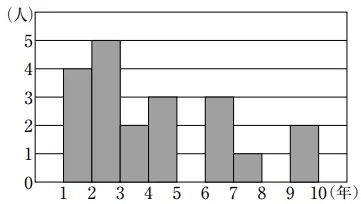
経験年数なのでヒストグラムを見る。
20人の中央値は10番目と11番目の平均。
3~4年の階級に含まれる。【3】
ⅱ
選択肢が込み入っている(;´Д`)

データを昇順に並べる。
(以下、中央値…Q2、第1四分位数…Q1、第3四分位数…Q3と記す)
●3年未満
【2・3・4・5・5・5・6・9・10】9人
最小値…2、最大値…10、Q2…5、Q1…3.5、Q3…7.5、最頻値…5
●3年以上
【3・3・4・4・5・5・6・8・8・8・9】11人
最小値…3、最大値…9、Q2…5、Q1…4、Q3…8、最頻値…8
【a】
中央値は5で等しく、最頻値は3年以上が大きい。
平均値の算出には時間がかかるが、中央値が違うので平均値と最頻値の組み合わせである。
ここから1~3に絞る。
【b】
1:最大値は3年未満の方が大きい。×
2:Q1・Q3ともに3年以上の方が大きい。〇
3:5本以上は3年未満が6/9、3年以上が7/11で3年未満の方が割合が大きい。×
【2】
(ウ)ⅰ
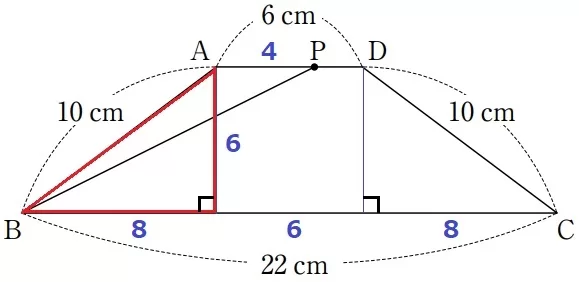
四角形ABCDは等脚台形。
上底6cmを下におろし、対称性から左右は(22-6)÷2=8cm
赤線の直角三角形は辺の比が3:4:5→等脚台形の高さは6cm
△ABPの面積は、4×6÷2=12cm2 【2】
ⅱ
6≦x≦16のときの式を求める。
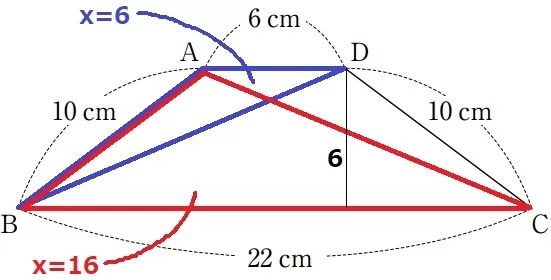
PがDにあるx=6のとき、y=6×6÷2=18
PがCにあるx=16のとき、y=22×6÷2=66
(6、18)→(16、66)
右に10、上に48だから、傾きは48/10=24/5
【5】y=24/5x-54/5、【6】y=24/5x+18に絞られる。
x=6を代入するとy=18になる【5】
(エ)
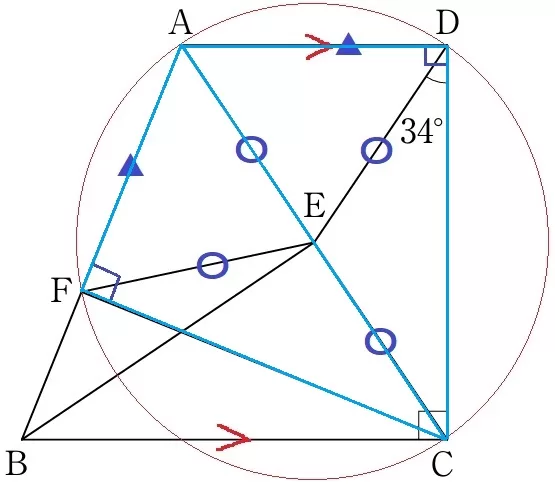
AD//BCから、∠ADC=90°
∠AFC=∠ADC=90°に着目する。
半円の弧に対する円周角は直角→直径をAC、中心をEとする円を描くと、
4点A・F・C・Dは同一円周上にある。
半径からAE=FE=CE=DE
さらに、AD=AF、共通辺ACと合わせると、
斜辺と他の1辺が等しい直角三角形ゆえ△ADC≡△AFC
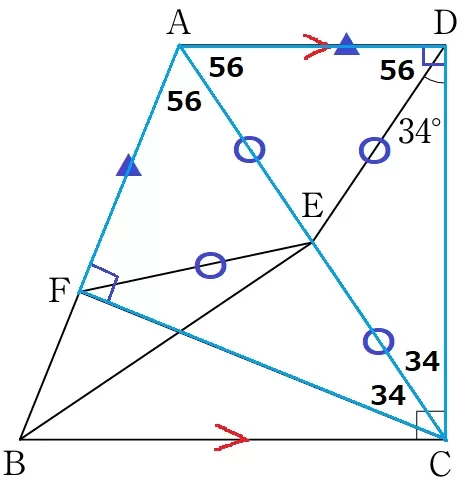
二等辺ECDと合同→∠EDC=∠ECD=∠ECF=34°
二等辺EADと合同→∠EDA=∠EAD=∠EAF=90-34=56°
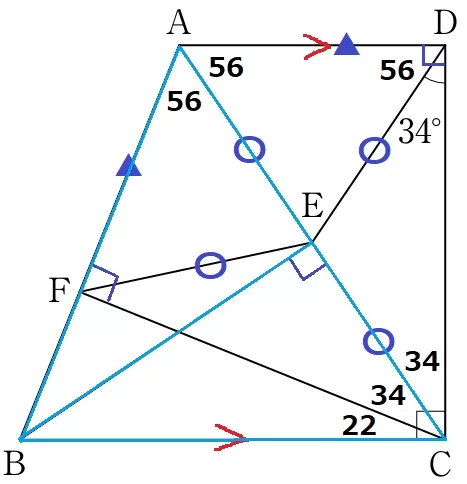
∠FCB=90-34×2=22°
ここで、△BACに着目すると∠BAC=∠BCA=56°(錯角の∠CAD=∠ACB=56°でもOK)
Eは二等辺三角形の底辺ACの中点だから、BE⊥ACがいえる。
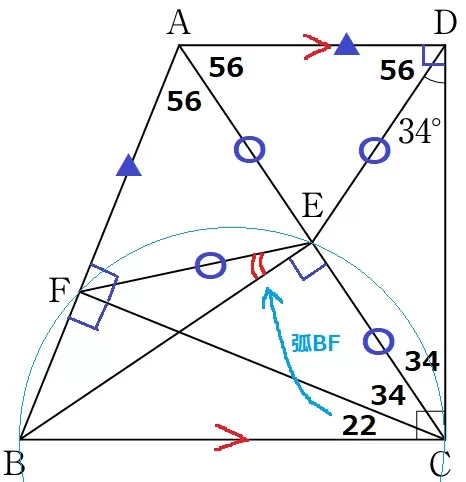
∠BFC=∠BEC=90°から、直径をBCとする円を描くと、
4点B・C・E・Fは同一円周上にある。
弧BFの円周角より、∠BCF=∠BEF=22°
大問4(関数)
(ア)
y=1/6x+5にx=-6を代入→A(-6、4)
これをy=ax2に代入。
4=36a
a=1/9 【1】
(イ)
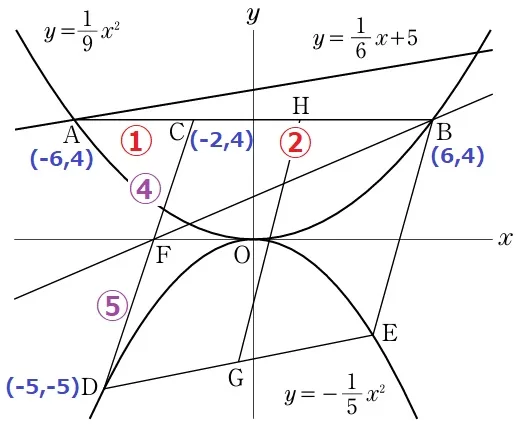
Bはy軸についてAと対称→B(6、4)
AC:CB=1:2から、C(-2、4)
y=-1/5x2にx=-5を代入→D(-5、-5)
CとDのy座標から、CF:FD=④:⑤
x座標の差3=⑨なので、⑤=5/3
Fのx座標は、-5+5/3=-10/3
F(-10/3、0)→B(6、4)
xの増加量は10/3+6=28/3、yの増加量は4。
傾き(変化の割合)は、4÷28/3=3/7
Fから右に10/3、上に10/3×3/7=10/7移動すると切片。
y=3/7x+10/7
ⅰ…【1】、ⅱ…【4】
(ウ)
最初の発想で決まる。
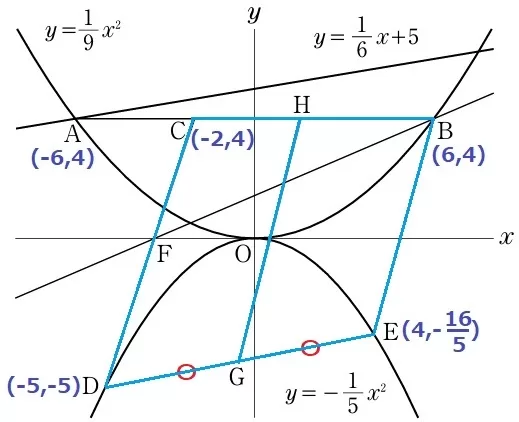
E(4、-16/5)
四角形CDGHと四角形BHGEが等積。
整数値が多いが、直線の式やG座標を求めようとすると分数が出てくる。
DG=GEを活用する方法はないか。
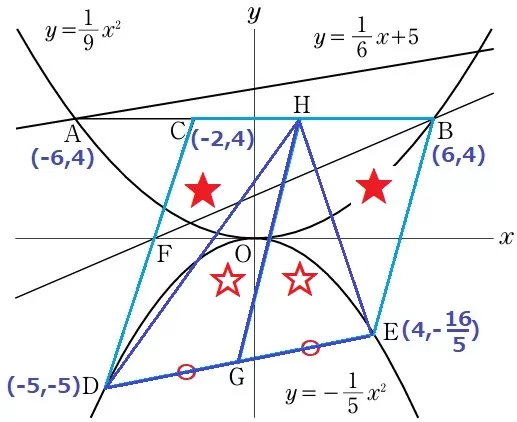
HD、HEに補助線。
△HDGと△HEGは底辺と高さが等しいから等積。
ということは、残りの△CDHと△BEHも等積である。
高さの比は、△CDH:△BEH=(5+4):(16/5+4)
=9:36/5=5:4
底辺の比は逆比で、CH:HB=④:⑤
Hのx座標は、{6-(-2)}×④/⑨+(-2)=14/9
大問5(確率)
(ア)
操作2でPの面積が決まる。
ab=6の組み合わせは、(a、b)=(1、6)(2、3)(3、2)(6、1)
全体は6×6=36通りだから、確率は4/36=1/9
(イ)
Qが最も大きくなる。
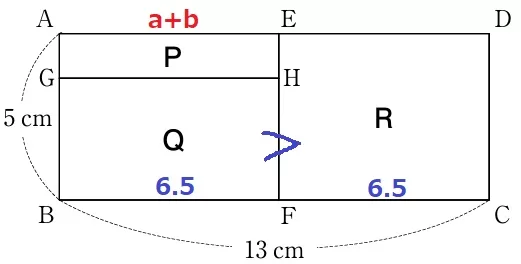
Q>Rとなるには、AEが最低でも6.5cmを超えなければならない。
aとbは自然数だから、a+b≧7である。
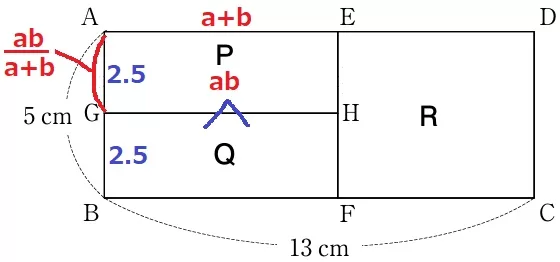
Q>Pとなるには、AGが2.5cm未満でなければならない。
AGはPの縦の長さだから、AG=ab/(a+b)<2.5
両辺を(a+b)倍すると、ab<2.5(a+b)
…これで範囲を絞られるかなと思ったのですが、実際にやってみるとうまくいきませんでした(;´Д`A
時間が絶望的に足りないなか、PQRそれぞれの面積を機械的に何度か出さないとダメなようです。
もっとも、36通りすべてを調べ上げるのは非現実的なので、少しでも作業量を減らしていきます。

まず、a+b、abはaとbをひっくり返しても値は変わらないので、この15通りは調べなくていい。
例えば、(3、4)と(4、3)は同じ。
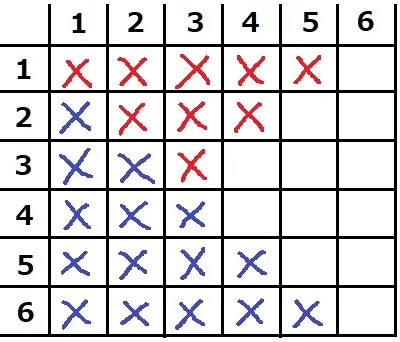
a+b≧7から9通りも外れる。

ab<2.5(a+b)
a+bの最大値は12なので、これを上の式に代入すると、
ab<2.5×12=30
(5、6)(6、6)が外れる。
10個も残る(;´Д`)
頑張って10個調べてもよいですが、AEをもう少し検討します。
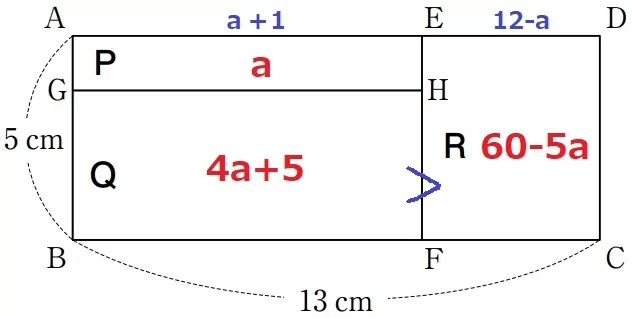
積abが一定のとき、和のa+bが最も大きくなるのは1が含まれるとき。
ab=6であれば、(2、3)より(1、6)の方が和が大きい。
高さ5cmのRが最も大きくなりやすいので、仮にb=1とおき、
AEが何cmを超えればQ>Rとなるか調べる。
AE=a+1、ED=13-(a+1)=12-a
Q=四角形ABFE-P=5(a+1)-a=4a+5
R=5(12-a)=60-5a
Q>Rより、
4a+5>60-5a
a>55/9=6・1/9(aは6を超えるが、便宜上b=1とおいたので続けます)
a+1>7・1/9
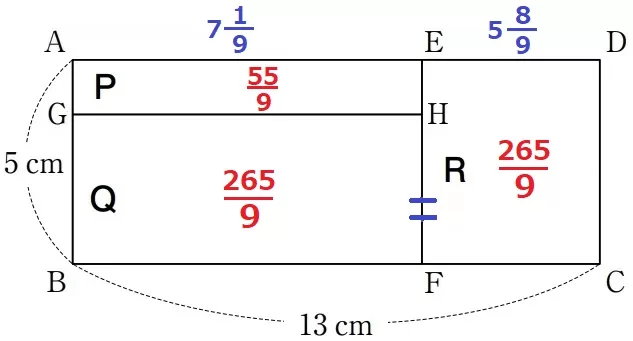
つまり、AE=7・1/9cmのときにQ=Rとなる。
a・bは1~6の自然数だから、a+b≧8となる。
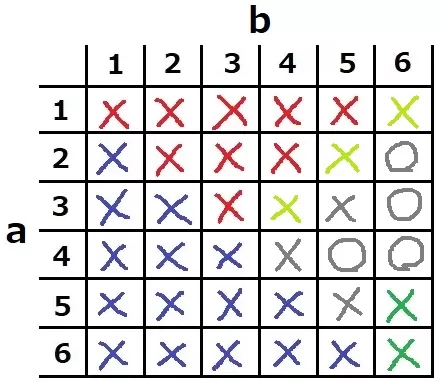
a+b=7の3つが消える。しかし、残りの7個は絞れませんでした。。
調べていくコツは和が一定の斜めでみる。
(2、6)だとP=12、Q=28、R=25で〇
(3、5)はP+Q=40、R=25は変わらない。P=15、Q=25で×
自動的に(4、4)も消える。(これ以外は自動で消せないが…)
地道に調べていくと(a、b)=(3、5)(4、4)(5、5)が不成立。
条件に合うのは(a、b)=(2、6)(3、6)(4、5)(4、6)
およびこれらの逆である(6、2)(6、3)(5、4)(6、4)の8通り。
確率は8/36=2/9
*範囲をうまく絞れたクレバーな方がいらっしゃいましたら、
ぜひコメント欄かお問い合わせよりお知らせ願います。
大問6(空間図形)
(ア)
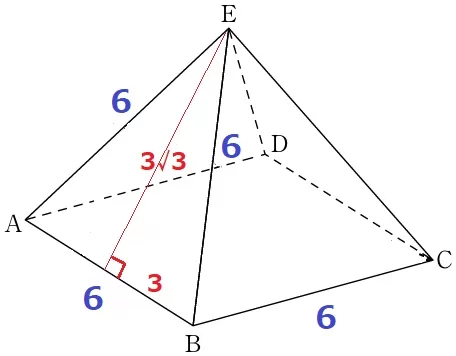
底面は1辺6cmの正方形、側面は1辺6cmの正三角形。
正四角錐の表面積は、6×6+6×3√3÷2×4=36+36√3cm2 【6】
(イ)
試験時間内では無理→△(コメ欄から助けを得ました。後述します)
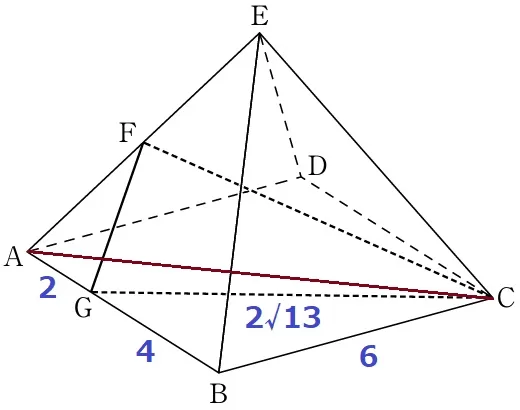
△BCGで三平方→GC=2√13cm
△FGCの高さを求めたいが、面FGCが斜めに傾いているので至難。
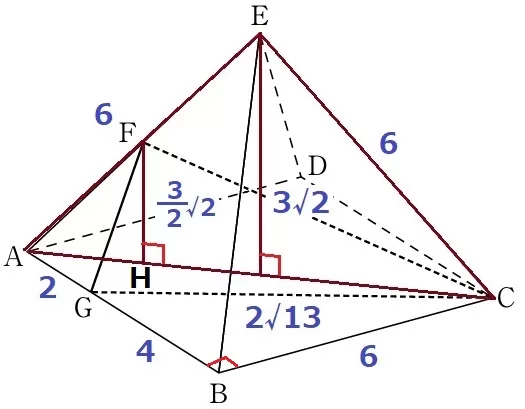
点Fを含む面AECに着目してみる。
△AECは等辺が6cmの直角二等辺三角形(△ABCと3辺が等しく合同)
△ABCは辺の比が1:1:√2→AC=6√2cm
対角線ACの半分である3√2cmが正四角錐の高さにあたる。
Fから垂線をおろし、足をHとすると、FはAEの中点だからFH=3√2/2cm
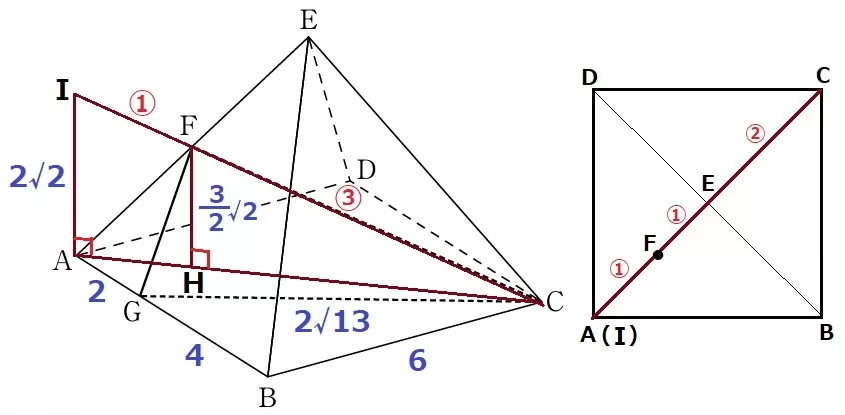
CFを延長、Aの真上をIとする。
図形を真上から眺めると、IF:FC=①:③
△FHC∽△IACより、IA=3√2/2×④/③=2√2cm
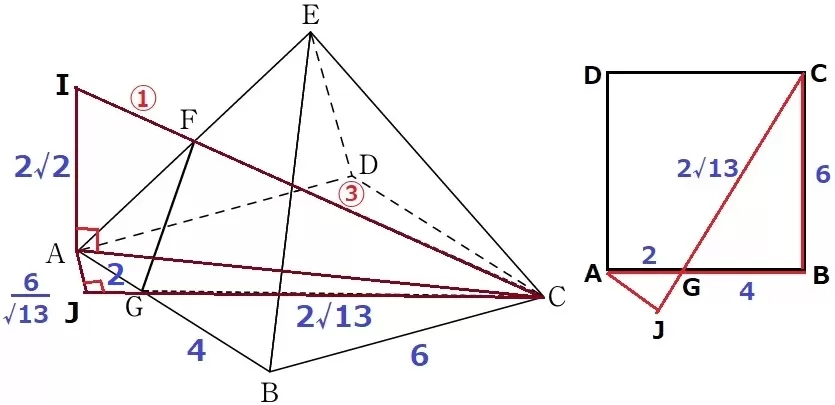
CGを延長、Aからおろした垂線との交点をJとする。
今度は図形の底面に注目する。
△AGJ∽△CGBより、AJ=2×6/2√13=6/√13cm
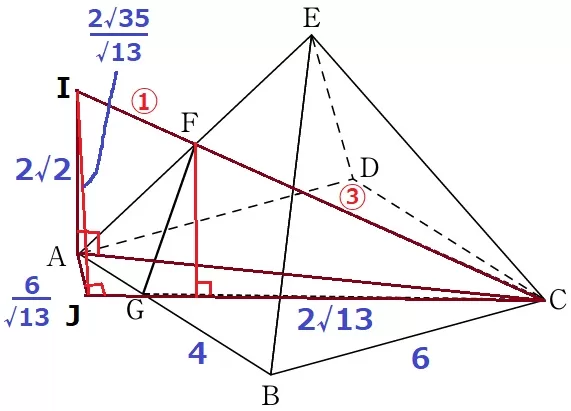
IJを結ぶ。
AJ⊥JC、IA⊥AJ→面IAJ⊥JC→IJ⊥JC
△IAJで三平方→IJ=√140/√13=2√35/√13cm
これを③/④倍すると、念願の△FGCの高さが求まる。
△FGCの面積は、2√13×(2√35/√13×③/④)÷2=3√35/2cm2
*正直、正規ルートなのか自信ありません。
良い解法を見つけた方は、コメント欄かお問い合せよりお知らせ願います。
@別解@
コメ欄にてピヨさんから素晴らしい指摘がございました。
△FGCの3辺の長さを求めます。
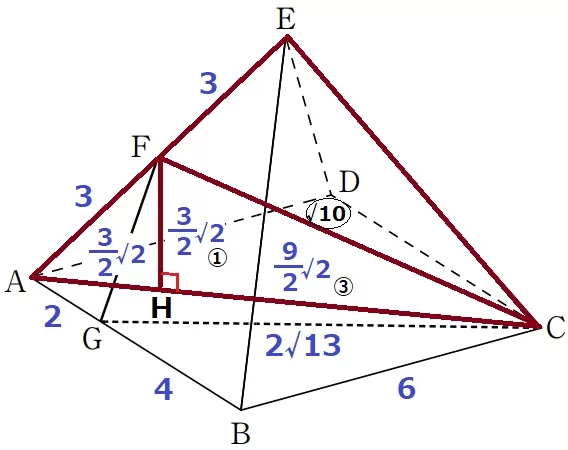
CG=2√13cm、FH=3√2/2cmまでは先ほどと同様です。
△AECは直角二等辺→△FAHも直角二等辺です。
AH=3√2/2cm
HC=AC-AH=6√2-3√2/2=9√2/2cm
△FHCで三平方→辺の比は①:③:〇√10なので、FC=3√2/2×〇√10=3√5cm
(*うーさんからコメントを頂きました)
△CEFの三平方でFC=3√5cmと出した方が早かったです。
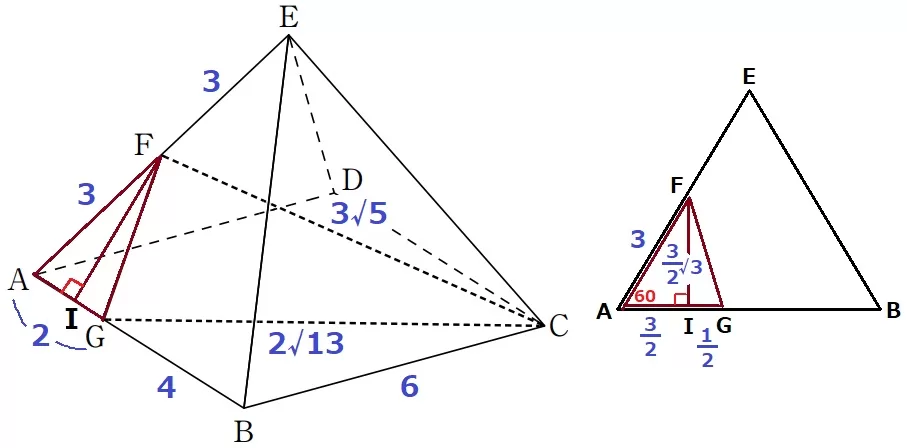
△EABは正三角形→∠EAB=60°
Fから垂線をおろし、足をIとします。
△FAIは1:2:√3の直角三角形なので、AI=3/2cm、FI=3√3/2cm
IG=2-3/2=1/2
△FIGで三平方→FG=√7cm
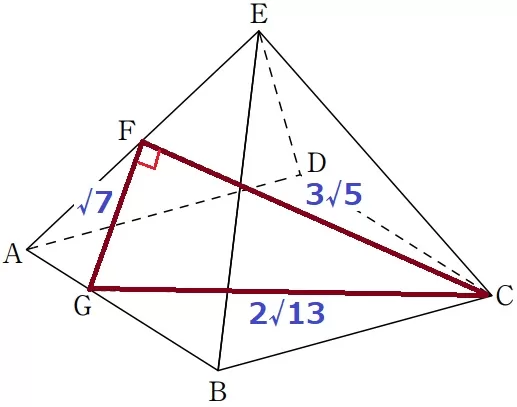
三角形の3辺がわかれば、Fから垂線をおろし、左右で三平方の方程式を立てると高さもわかるのですが、
根号の中身が違うので気づきにくいですけど、結論からいうとGF2+FC2=GC2が成り立ちます。
(√7)2+(3√5)2=52=(2√13)2
三平方の定理の逆より∠GFC=90°なので、3√5×√7÷2=3√35/2cm2
●講評●
全体の内容量、構成のバランスが極めて悪く、完走をするのに50分では到底間に合わない。
過去問の対策を怠っていなければ50点は稼げるが、70点以上をとるのは厳しい。
大問1
配点15点。確実に死守したい。
大問2
配点24点。ここまでで40点近く取れる。
(エ)短い方の1辺をxとおく。
(オ)中心角を出さずに1/9円と割合で出しておくといい。
(カ)一般的に正答率の低いタイプだが、過去問の踏襲。
大問3
(ア)ⅰ:時間が足りないので、必要な箇所だけ読む。
ⅱ:パス推奨。厄介なポイントがBFの長さ。
今年の千葉(正答率5.7%)で似た要素が出ているが、千葉以上に見えずらい構図で処理も多い。
(イ)ⅱ:せめて資料は昇順に載せておくべき。並び替える時間すら惜しい試験。
9択もあるが、手際よく判断すれば選択肢は絞りやすい。
(ウ)ⅱ:70点に達するには、このレベルでも必答になる。
D→Cの変化の割合を求める。
(エ)ここも難しい。
右上から左下へ向かう流れ。踏むべき段数が多い。
直角から円を見る、合同、二等辺の垂線とバラエティ豊か。
大問4
(イ)2問目としては処理多めでも、なるべく正解したい。
(ウ)四角形の等積。
G座標が分数なので、これを起点にしようとすると泥沼にハマる。
DEが斜めで見えにくいが、四角形を分割した三角形の等積が使える。
大問5
(ア)積だけでいい。
(イ)難。
結論から条件に合うのは和が8~10、積が12~24の範囲だが、
(3、5)のように合わない組み合わせもでてくるので、おそらく調査を余儀なくされる(-_-;)
長方形を書きまくって調べるしかないのであれば、もう時間が無い。諦めていい。
大問6
(イ)三角形の3辺の長さがわかれば三平方で面積が求まるものの、いかんせん計算量が多い。
サボは面AECと面FGCを拡張して、どこで三平方が使えるか→Aを頂点とする直角三角形と着想したが、
推奨できる解法かは疑問。。配点は6点と高いが、見直しに費やした方が賢明。
本試験から約1週間後でこうも難易度が著しく上がってしまうと、
とくに難関校を狙う層は多少無理してでも本試験を受けるべきとアドバイスせざるを得ないのでは?


コメント
最後の(イ)は△FGCの三辺を求めると、GC^2=GF^2+FC^2が成り立つので直角三角形の面積を求めるだけなのではないでしょうか!
FGを求めるのが大変かもですが。
コメントありがとうございます。
あああ!本当だ・・。気づきませんでした。
FG=√7で計算すると、3√35/2cm2になりました。
あとで追記させてもらいます。助かりました(*_*)
問3の(エ)でなぜEがACの中点になるか教えてください
コメントありがとうございます。
直径をAC、中心をEとする円を描くと、4点A・F・C・Dは同一円周上にあるので、
半径よりAE=ECがいえます。
これは高校数学で塾で齧ってる勢が得してしまう感じですかね
△CFHから三平方でCFが分かり、三角比が使えればFGも分かるのでヘロンの公式が使えちゃいますね
最後の問題、三角形の三辺の長さが分かったけど、直角三角形ということに気づかず、CGを底辺として高さを三平方でゴリゴリ求めたら、3√455/26になってしまいました(答えはあってた)。わざとなんですかね?これで5点はひどすぎます‼️
コメントありがとうございます。
私も直角に気づかず、イライラしながら三平方ごり押しで高さを求めたらミスりました。
メールをくださった方も50分で解く内容ではないとおっしゃっていました。
これを作った人および承認した人に50分でやってみろと言いたいですね(ꐦ°᷄д°᷅)
FGを求めるのは三角比を使っちゃえば簡単ですが、中学生には難しいですかね
コメントありがとうございます。
FGは側面でFから垂線をひくと三平方で比較的求めやすかったです。
ヘロンも考えましたが、ルートの中身が異なる3つの無理数なので厳しいかなと。
この問題はとりあえず期待を込めて3辺を求めてみる→三平方が成り立ってラッキーという流れでしょうか。
うむむ・・難儀を感じます。。
平面図形が苦手な子は可哀想なセットでしたね……(得意でも難しいけど)
コメントありがとうございます。
3アⅱの難所は今年の千葉で最も難しかった図形と似ているのですが、
千葉よりも処理過程が多いのにこの位置にいることに目が点になりました。
2017の大阪府C問題みたいな絶望感が漂う……あの時は合格者の平均点でさえ90点中25点くらいの鬼畜っぷりでしたが、これは追検査とはいえレベルに関係ない一般での試験ですからね……平均点がもし発表されれば知りたいですが、たぶん無理なのでしょうね。神奈川県は作問のバランス調整があまり上手くないんですかね?
コメントありがとうございます。
そんなヤバイ問題があったのですか!あとで探してみます。
2までは過去問の踏襲なので40~50点まではいけそうですが、70点以上はほぼいないでしょうね。本試験と違い、残念ながら平均点の公表はございません。神奈川の数学は本試験も乱高下があり、追検査は何度か苦しめられました(´Д`)こうも難度の差があると、多少の風邪気味なら本試験を受けるべきになっちゃいそうです。
今更かもしれませんが、大問5の(イ)は範囲の絞り方を間違っていると思います。
PがQより小さくなる条件は問題ないのですが、a+b>=7はRよりQが小さくなる条件を十分に満たさないはずです。例えば(4,4)の場合もP,Q,Rの面積は16,24,25で条件を満たせていません。
全体的に難易度が高かったですね。解説の作成お疲れさまです。
コメントありがとうございます。
(4,4)ダメですね…。のちほど解法を再考してみます。
ご指摘ありがとうございました。
問6(イ)の別解のように3辺を求める方法ですが、CFの長さは、AC=6√2と分かった時点で、三角形AECが1:1:√2の三角定規の比が使えるので、角AECが90度と分かり、CFは3と6の三平方の定理で3√5と求められる方法もありました。
にしても難しい…笑
コメントありがとうございます。
△CEFに注目した方が圧倒的に3√5が出しやすいですね!
あとでお名前をご紹介したうえで本記事に付記させてもらおうと思います。
他に何か気づいたことがありましたら気兼ねなくコメントしてください。
サボ