平均24.7点(前年比;-0.2点)
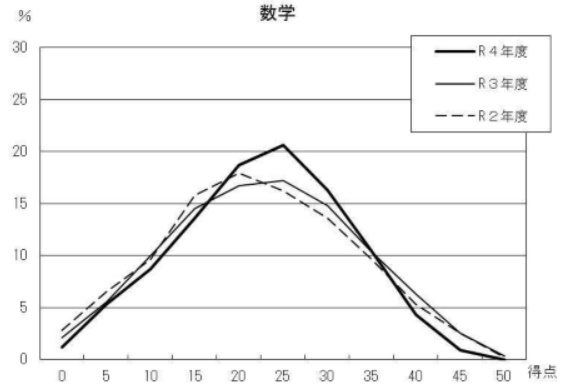
問題はこちら→リセマムさん
大問1(小問集合)
(1)
(-2)×3-4
=-6-4
=-10
(2)
140=22×5×7
(3)
6/√3+√15÷√5
=2√3+√3
=3√3
(4)
a÷10=b…3
a=10b+3
(5)
x-3y=5 …①
3x+5y=1 …②
①×3-②をすると、-14y=14
y=-1
①に代入して、x=2
x=2、y=-1
(6)
x2+x-6
=(x+3)(x-2)=0
x=-3、2
(7)
有理数→整数の分数で表せる数。
無理数→整数の分数で表せない数。
0.5=1/2〇、1/3〇。√2×、√9=3=3/1〇
π=3.141592…循環しない無限小数は無理数×
ウ・オ
(8)
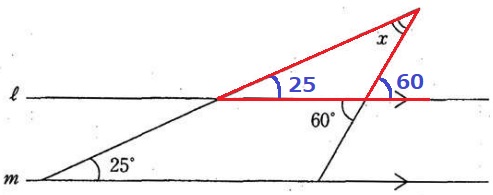
同位角と対頂角で角を移動する。
赤線で外角定理→x=60-25=35°
(10)
抽出した200個のうち、白:黒=180:20=⑨:①
黒は全部で100個だから、白全部は100×⑨=900個
イ
(11)
全体は、6×6=36通り
1/12=3/36
結果が3通りとなる事象が答え。
●和が1→×
●和が2→1+1
●和が3→1+2、2+1
合計が3通りになるのは、和が3以下
大問2(データの活用・数量変化)
(1)①【1】
最頻値(モード)は最もあらわれている値。
13.0~13.5の階級値である13.25秒
【2】
13.0秒未満は、1+1+2+4=8人
8÷20=40%
②

ア:最小値はミナトの方が小さい。〇
イ:範囲(レンジ)=最大値-最小値、ミナトの方が大きい。
しかし、四分位範囲=Q3(第3四分位数)-Q1(第1四分位数)はユウキの方が大きい。×
ウ:中央値(Q2)に着目する。20回の中央値は10番目と11番目の平均。
2人とも中央値が9.0を超えるので、9.0m以上の記録は少なくとも10回はある。〇
エ:20回のQ1は5番目と6番目の平均。5番目と6番目が8.5mのとき、8.5m以下は6回になる。×
ア・ウ
(2)①
8000+20×200=12000円
②
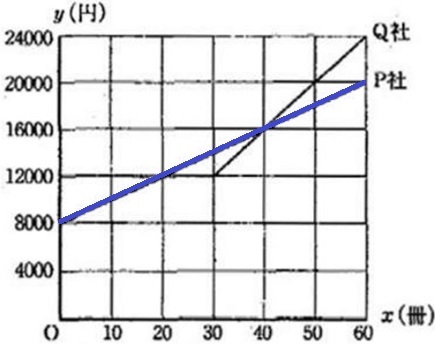
基本料金は8000円→切片は8000
傾きは200。右に20進むと、上に4000あがる。
(20、12000)(40、16000)(60、20000)を通過する。
③
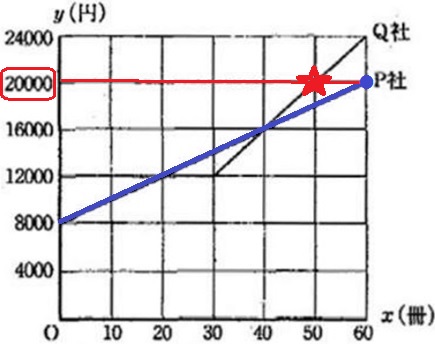
先ほどのグラフを用いる。
Q社50冊は★だから20000円
P社20000円は●で60冊
④
1冊あたりの料金が400円となる冊数をxとする。
印刷料金を2通りで表して等式を立てる。
8000+200x=400x
x=40
40冊以上
@余談@
こう考えることもできる。
1冊あたりを400円にしたい。
1冊追加するたびに200円かかるから、残りの200円で基本料金8000円を分割払いすればいい。
8000÷200=40冊
大問3(規則)
(1)①
2番目…4枚
3番目…8枚
4番目…12枚→4(4-1)
5番目…16枚→4(5-1)
6番目は20枚
②
n番目は、4(n-1)=4n-1枚
問題文をよく読もう!『n番目の次の図形をつくるとき』→つまり、n+1番目。
nがn+1に置き換わるので、4(n+1-1)=4n枚
@余談@
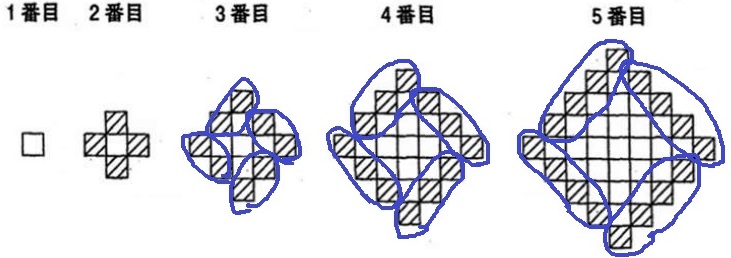
n番目が4(n-1)になるのは、魔方陣の考えから説明できる。
②

5番目のとき、白25枚、黒16枚。
白だけをみると縦5枚、横5枚で25枚。
黒だけをみると縦4枚、横4枚で16枚。
n番目は偶数か奇数かわからなくても、
外側と同じ色の芝生はn2枚で、あいだに挟まれる色は(n-1)2枚。
n2+(n-1)2
=2n2-2n+1枚
(3)

計算では、30m÷30cm=100枚並べられるが、
真ん中の縦列をみると、【1、3、5、7、9…】といずれも奇数。
100未満の最大奇数である99枚まで芝生を並べられる。
99は何番目の奇数か?⇒(99+1)÷2=50番目
A…99、B…50
大問4(関数)
(1)①
Bはy軸に関してAと対称関係にある。
-6
②
y=1/4x2にx=6を代入して、Aのy座標は9
xの値が0から6まで増加するときの変化の割合→OAの傾き。
原点O→A(6、9)
右に6、上に9移動するから、傾きは9/6=3/2
(2)①

菱形の対角線はおのおのの中点で交わる。
Aのy座標を2倍してP(0、18)
菱形OAPBの面積は、対角線AB×対角線PO÷2=12×18÷2=108
②
等積変形からPC//BA→Cのy座標は18
OC;y=3/2xにy=18を代入して、x=12
C(12、18)
(3)①
y=-12/xにy=-3を代入して4
②【1】

平行四辺形の対辺は等しい。QR=ED=4
DとEはy軸について対称→Dのx座標は2
これをy=1/4x2に代入して、D(2、1)
【2】
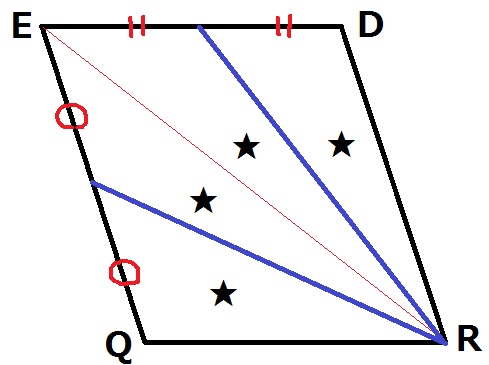
対角線ERは平行四辺形DEQRを2等分する。
辺EDの中点か辺EQの中点を通れば3:1に分けられる。
(もしくは、点(0、1)か点(-1、-1)を通過するでもOK)
大問5(平面図形)
(1)
半径と接線は直交する。
∠OPA=90°
(2)
接線の作図。

∠OPA=90°を使う。
半円の弧に対する円周角OPA=90°と捉えれば、AOを直径とする円周上にP、P’がある。
①AOの垂直二等分線。中点が円の中心。
②円を描き、円周と円Oが交わる2点がPとP’
(3)
AP=AP’(接線の長さは等しい)証明。
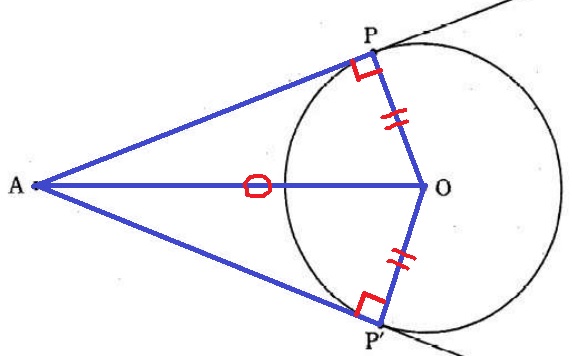
半径と接線は直交する。∠OPA=∠OP’A
半径OP=OP’、共通辺OA。
斜辺と他の1辺が等しい直角三角形から△OPA≡△OP’A
対応する辺からAP=AP’
②
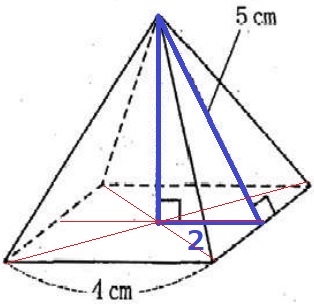
2角相等で△PAM∽△OPM
求めたいPMの長さをxとおく。
AM:MP=PM:MO
3:x=x:1
内項と外項の積で、x2=3
x>0、x=√3
PM=√3cm
③
∠PRP’は120°を維持しながら動く→円周角の定理

↑RがAO上にある場合を考えてみる。(上下対称)
P・R・P’を通る円の中心をQとする。
Rを含まない弧PP’の円周角PRP’=120°
その中心角は∠PQP’=120×2=240°
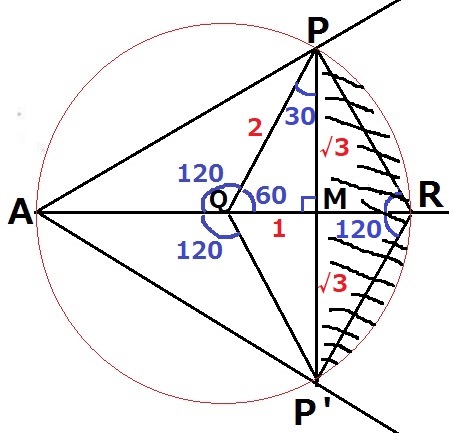
求積すべき図形は斜線部分で扇形PQP’から△PQP’をひけばいい。
△PQMの内角は30°-60°ー90°で辺の比が1:2:√3。
前問よりPM=MP’=√3、QM=1、PQ=2
2×2×π×1/3-2√3×1÷2
=4/3π-√3
●講評●
大問1
基本レベルゆえ、ほぼ正解したい。
(4)割り算の式に整理するとわかりやすい。
(10)抽出した標本200個での黒:白の割合は母集団でも同じとみなす。
(11)分母を36にして、3通りの結果になるものを探す。”以下”に注意。
大問2
(1)②四分位範囲は箱の長さ。四分位範囲が大きいとデータのばらつきが大きい。
(2)小問が続く。よくある形式で、難易度も易しい。
④求めたい冊数をxとおいて方程式。
大問3
(1)②問題が意地悪な感じがする( ゚A゚)
(2)②白か黒かで分けるとややこしいと思う。
n番目はn2枚と(n-1)2枚が上にくるか下にくるかの違いで和は同じ。
(3)最後の問題は解きやすかった。落とすともったいない。
大問4
座標が整数値で処理が楽だった。
小問数はあるが、得点を稼いでおきたい。
(3)②【2】平面図形の問題。
大小を入れ替えれば2通りあるが、どちらでも良い。
大問5
(2)円外の点からの接線の作図はとっさに出ないと苦労する。
(3)証明も平易だった。
(4)②直角三角形の頻出の相似。いたるところで出てくる。
③円周角の定理を想起する。中心角は240°、有名角を頼りに長さを求める。





コメント