2021年度　山梨県公立高校入試問題過去問【数学】解説

平均59.1点（前年比；＋5.2点）
最高点100点、最低点０点。

問題はコチラ→ＰＤＦファイル
出題範囲の除外は標本調査。

大問１（計算）

（１）　98％
（－13）＋（－８）
＝－13－８
＝－21

（２）　85％
（１/６－４/９）×18　←分配法則
＝１/６×18－４/９×18
＝３－８
＝－５

（３）　90％
－４²＋７²
＝－16＋49
＝33

（４）　90％
√10×√２＋√５
＝２√５＋√５
＝３√５

（５）　96％
56ｘ²ｙ÷（－８ｘｙ）
＝－７ｘ

（６）　83％
６ｘ＋７ｙ－２（ｘ＋３ｙ－９）
＝６ｘ＋７ｙ－２ｘ－６ｙ＋18
＝４ｘ＋ｙ＋18

大問２（小問集合）

（１）　87％
ｘ²－７ｘ－18
＝（ｘ＋２）（ｘ－９）＝０
ｘ＝－２、９

（２）　92％
対称の軸の作図。
ＡとＢは対応する点⇒ＡＢの垂直二等分線が対称の軸となる。

（３）　77％

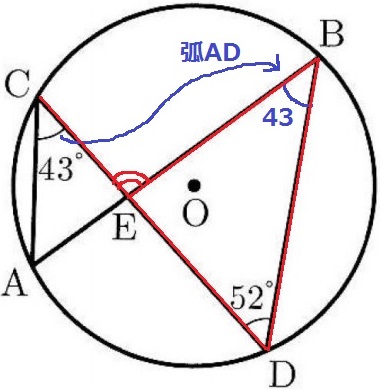
弧ＡＤに対する円周角で、∠ＡＢＤ＝43°
△ＢＤＥで外角定理→∠ＣＥＢ＝43＋52＝95°

（４）　67％
反比例の比例定数ａは積ｘｙで一定。
ｙ＝－３×５÷12＝－５/４

（５）①　74％
最頻値（モード）は最もあらわれている値。
10～20分の階級の階級値⇒15分

②　78％
０～20分の度数は７＋９＝16
相対度数は、16÷32＝0.5

大問３（数量変化）

（１）　80％
ｘが時間でｙが道のり。
一次関数のグラフは直線で、傾きが速さである。
グラフが直線⇒変化の割合が一定⇒速さが一定。
ウ

（２）　73％
ｙ＝４/３ｘにｙ＝20を代入。
20＝４/３ｘ
ｘ＝15（０≦ｘ≦48）
９時15分

（３）ｸﾞﾗﾌ…26％！（部分点42％）、式…42％（部分点15％）
求め方を記述する。
■グラフから求める方法
列車Ｐと列車Ｑの交点の座標を求める。
■式から求める方法
①と②の連立方程式を解く。
*「交点を求める」だけだと減点対象。

（４）　９％!!

列車Ｐと列車Ｑのグラフをみると、下の部分が二等辺三角形に見える。
Ｐの傾きは３/４→右に④上に③移動。
Ｑの傾きは－３/４→右に④下に③移動。
右上がりと右下がりの度合いが対称的⇒左右対称で二等辺三角形である。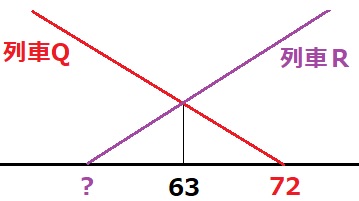
ＲはＰと傾きが等しいから、同様に二等辺三角形。
10時３分→ｘ＝63
二等辺三角形の頂角からおろした垂線は、底辺を垂直に二等分する。
72－63＝９分
63－９＝54分
９時54分

大問４（方程式）

（１）　82％
チーズ59kcalがｍ個、ビスケット33kcalが２枚。
59ｍ＋33×２
＝59ｍ＋66kcal

（２）カレー…25％！、サラダ…24％！
連立方程式。

カレーをｘｇ、サラダをｙｇとする。
800ｇで等式。
ｘ＋ｙ＝800…①

950kcalで等式。１ｇあたりのカロリーになおすこと！
１ｇあたりカレー1.3kcal、サラダ0.7kcal。
1.3ｘ＋0.7ｙ＝950
13ｘ＋７ｙ＝9500…②

②－①×７をして、ｘ＝650、ｙ＝150
カレーライス…650ｇ、サラダ…150ｇ

＠別解＠
もし、800ｇすべてがカレーだったら、130×８＝1040kcal
実際は950kcalだから、1040－950＝90kcal少なくすればいい。

カレー100ｇをサラダ100ｇに交換すると60kcal減るので、
交換すべき重さは、100×90/60＝150ｇ
つまり、サラダは150ｇ。カレーは800－150＝650ｇである。

（３）①　61％
『タンパク質だけ20ｇとる』なので、
４ａ＋９ｂ＋４ｃにａ＝20、ｂ＝０、ｃ＝０を代入。
４×20＋９×０＋４×０
＝80kcal

②記号…45％、説明…11％！（部分点26％）
解答では根拠を示して説明する。
総エネルギー量は、４×120＋９×60＋４×370
＝480＋540＋1480＝2500kcal

脂質のｴﾈﾙｷﾞｰ比率は、540÷2500×100＝21.6％
これは20％以上30％未満の望ましい範囲にある。（ア）

大問５（関数）

（１）　86％
ｙ＝１/８ｘ²にｘ＝－４を代入。
ｙ＝１/８×（－４）²＝２

（２）　49％（部分点27％）
△ＡＲＱ∽△ＣＰＱの証明。

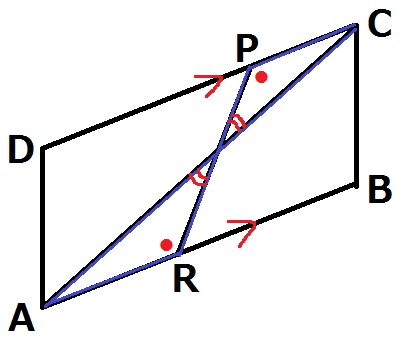
平行四辺形だけを抜き出せば、基本レベルの証明。
対頂角と錯角で２角相等→∽

（３）　51％

関数にｘ座標を代入して座標を確認。
Ｄ座標が不明。
ＡＢ//ＤＣなので、ＤＣと傾きが同じＡＢの式を先に求める。
Ａ（－４、２）⇒Ｂ（８、８）
右に12、上に６移動するから、ＡＢの傾きは６/12＝１/２
Ａから右に４上に２移動して、切片は２＋２＝４
ＡＢ；ｙ＝１/２ｘ＋４
ＢとＣのｙ座標の差が８だから、ＡＢをｙ軸方向に＋８平行移動すればＤＣになる。
ＤＣ；ｙ＝１/２ｘ＋12

（４）　４％!!

平行四辺形ＡＢＣＤを二等分する直線は、対角線ＡＣとＤＢの交点（各々の中点）を通る。
ＡＣの中点をＳとする。
ＡとＣの座標を平均してＳ（２、９）
ＯＰ（ＯＳ）の式は、ｙ＝９/２ｘ

Ｐはｙ＝９/２ｘとｙ＝１/２ｘ＋12の交点。
９/２ｘ＝１/２ｘ＋12
９ｘ＝ｘ＋24
ｘ＝３（Ｐのｘ座標）

ＤとＰのｘ座標の差は７、ＰとＣのｘ座標の差は５。
ＤＰ：ＰＣ＝７：５

大問６（空間図形）

（１）　80％（部分点１％）
三平方の定理。
√（８²－６²）
＝√28＝２√７ｃｍ

（２）①　79％
ネジレ→延長しても交わらない、かつ平行でもない。
ＡＢ・ＢＣ・ＡＯは一端がＡかＣだからＡＣと交わる。
残りのＢＤ・ＯＢはＡＣと交わらず、平行でもないのでネジレ。
ウ・オ

②　７％!!（部分点０％）

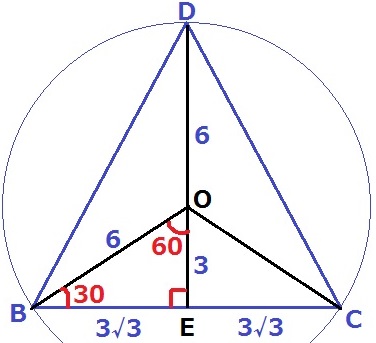
高さは出ているので、底面積を求める。
円周上に３点が等間隔→３つの弧の長さは等しい→３つの弦も等しい→△ＢＣＤは正三角形
ＤＯの延長線とＢＣとの交点をＥとする。
∠ＢＯＣ＝360÷３＝120°、ＤＥを境に左右対称だから、∠ＢＯＥ＝120÷２＝60°
△ＢＯＥの内角は30°－60°－90°で辺の比は１：２：√３。
ＯＥ＝３ｃｍ、ＢＥ＝３√３ｃｍ
正三角形ＢＣＤの面積は、６√３×９÷２＝27√３ｃｍ²
三角錐Ａ―ＢＣＤの体積は、27√３×２√７÷３＝18√21ｃｍ³

③　３％!!

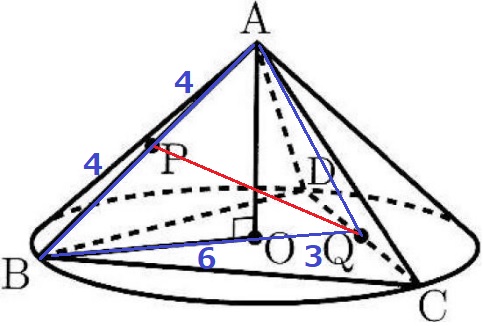
ＰＱは△ＡＢＱ上の線分だから、△ＡＢＱを切り取って考える。
ＰはＡＢの中点なので、ＡＰ＝ＰＢ＝４ｃｍ
前問の図よりＢＯ＝６ｃｍで、ＯＱは先ほどのＯＥと同じ３ｃｍ。

ここで、（１）ＡＯ＝２√７ｃｍを使う。
Ｐを通りＡＯに平行な線を引き、ＢＱとの交点をＦとする。
△ＡＯＢ∽△ＰＦＢの相似比は、ＢＡ：ＢＰ＝８：４＝２：１
ＰＦ＝２√７÷２＝√７ｃｍ
ＢＦ＝ＦＯ＝３ｃｍ
最後に△ＰＱＦで三平方→ＰＱ＝√43ｃｍ

④　０％!!!（部分点０％）
難問。
ここまでの見直しが済んで、時間を持て余した人用です。

Ｒ、Ｔ、Ｑは中点だから三角錐Ｃ－ＡＢＤ∽三角錐Ｃ－ＲＴＱの相似比は２：１。
△ＡＢＤと△ＲＴＱは平行で面積比は４：１、△ＡＢＤ：△ＰＢＳの面積比も４：１。
→△ＰＢＳと△ＲＴＱの面積比は等しく、かつ平行である。

問題は△ＰＢＳと△ＲＴＱが斜めに傾いている点。
もっとも、平行四辺形を切って貼り付けると長方形に変形できるように、
斜め柱体は垂直の柱体に置き換えることができる。
立体ＰＢＳ―ＲＴＱを底面△ＢＣＤに垂直な面で切りたい…。

ここで、（１）ＡＯ＝２√７ｃｍを活用する。
ＡＯは円錐の高さだから底面△ＢＣＤに垂直で、Ｏは正三角形ＢＣＤを２等分するＤＴ上にある。
そこで、ＡＴに補助線をひき、面ＡＴＤで切り取って考えてみる。

ＡＴとＰＲの交点をＧ、ＤＴとＳＱの交点をＨとする。
３辺の長さは前問の△ＡＢＱと同じで、ＴＤ＝ＢＱ＝９ｃｍ
△ＡＰＧ∽△ＡＢＴで、ＡＧ：ＧＴ＝１：１
同様に、△ＤＳＨ∽△ＤＢＴで、ＤＨ：ＨＴ＝１：１
ＧとＨはＡＴ、ＤＴの中点である。

△ＡＴＤ∽△ＧＴＨで、面積比は△ＡＴＤ：△ＧＴＨ＝４：１
△ＧＴＨの面積は、９×２√７÷２×１/４＝９√７/４ｃｍ²
斜め柱体ＰＢＳ―ＲＴＱは底面積が９√７/４ｃｍ²、高さＢＴ＝３√３ｃｍの柱体とみなせるから、
９√７/４×３√３＝27√21/４ｃｍ³

＠別解＠
実はサクッと出せる方法がある。
（２）で全体の三角錐Ａ—ＢＣＤを求めたので、ここから体積比で何とかできないものか。

ＡＤの中点をＵとする。
６点Ｐ、Ｑ、Ｒ、Ｓ、Ｔ、Ｕは三角錐Ａ—ＢＣＤの辺上の中点。
三角錐Ａ―ＰＲＵ（三角錐Ｒ―ＴＣＱ）∽三角錘Ａ―ＢＣＤの相似比は１：２。
体積比は相似比の３乗。
三角錐Ａ―ＢＣＤの体積比を⑧とすると、
三角錐Ａ―ＰＲＵと三角錐Ｒ―ＴＣＱの体積比は①。
また、△ＰＲＵと△ＳＱＤは合同。
三角錐Ａ—ＰＲＵと斜め三角柱ＰＲＵ―ＳＱＤの底面積は等しく、高さの比も同じ。
三角柱の体積は三角錐の３倍だから、斜め三角柱ＰＲＵ―ＳＱＤの体積比は③となる。
求積すべき立体は、⑧－（①＋①＋③）＝③
要するに、三角錐Ａ—ＢＣＤの３/８倍である。
18√21×３/８＝27√21/４ｃｍ³