平均22.9点(前年比;-5.5点)
最高点50点、最低点0点
問題はこちら→リセマムさん
出題範囲の削減はなし。
大問1(計算)
(1)
2-(-5)-4
=2+5-4
=3
(2)
3÷1/4×(-22)
=3×4×(-4)
=-48
(3)
3(4x-y)=6 ←÷3
4x-y=2
y=4x-2
(4)
√12-9/√3
=2√3-3√3
=-√3
(5)
xy-6x+y-6 ←6でまとめられそう
=xy+y-6x-6
=y(x+1)-6(x+1)
=(x+1)(y-6)
(6)
x2+5x+2=0
解の公式を適用、x=(-5±√17)/2
(7)
絶対値は、数直線において原点0からの距離。
小さい順に、0→2→-3
イ→ウ→ア
大問2(図形)
(1)
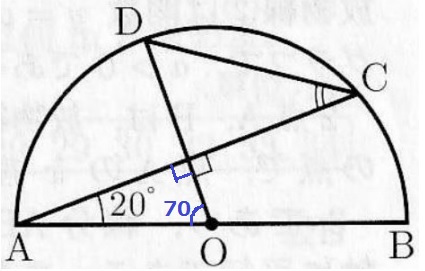
下の三角形で外角定理、∠AOD=90-20=70°
∠ACDは弧ADに対する円周角だから、70÷2=35°
(2)(ア)
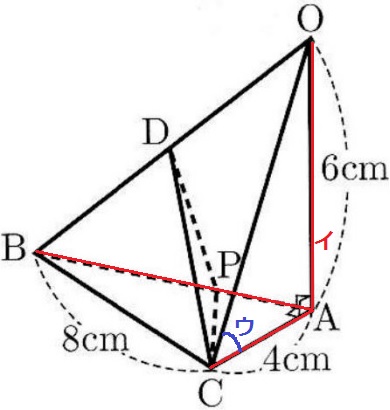
ア:∠OCA=60°である
→仮に∠OCA=60°であれば、直角三角形OACの辺の比は1:2:√3だが、
CA:AO=1:√3ではない。×
イ:面OAB⊥面OAC
→∠BAC=90°からいえる。〇
ウ:辺OC⊥面ABC
→△OACにおいて∠OAC=90°から、∠OCA≠90°でいえない。×
エ:OA//CD
→OAは面OAC(もしくは面OAB)上の線分、CDは面OBC上の線分である。
面OACと面OBCは平行ではない。×
イ
(イ)

三角錐OーABCと三角錐DーABCは底面が△ABCで共通。
体積比は高さの比に相当する。
三角錐O―ABCの体積を【1】とすると、
DがOBの半分だから、三角錐D-ABCの体積は【1/2】
三角錐D—BCPの体積は【1/3】だから、
三角錐D—APCの体積は【1/2】-【1/3】=【1/6】
これらの三角錐は高さが共通するので底面積の比が体積比になる。
△BCP:△PCA=【1/3】:【1/6】=2:1
△BCPと△PCAは高さが共通だから、底辺のBP:PC=②:①
△ABCで三平方→辺の比が1:2:√3の直角三角形でAB=4√3cm
BP=4√3×②/③=8√3/3cm
(3)
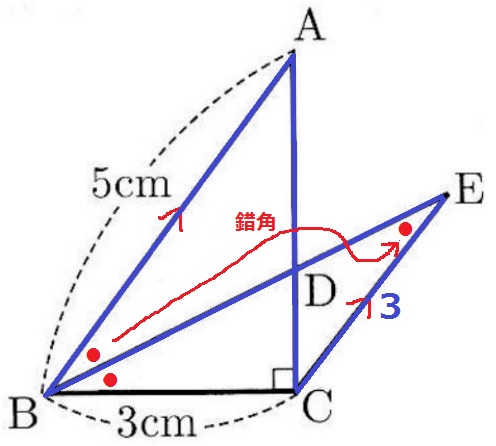
AB//ECから錯角で∠BEC=●
△BCEは2つの底角が等しい二等辺三角形→CE=3cm
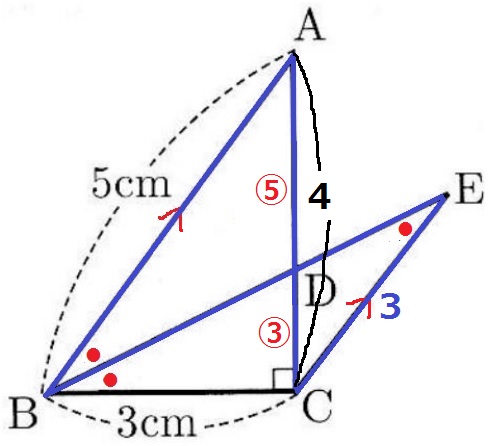
△ABCは3:4:5の直角三角形→AC=4cm
△ABD∽△ECDより、AD:DC=⑤:③
DC=4×③/⑧=3/2cm
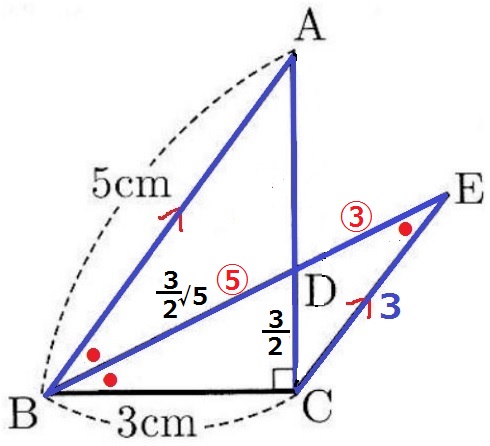
△BCDで三平方→BD=3√5/2cm
BD:DE=⑤:③だから、
BE=3√5/2×⑧/⑤=12√5/5cm
大問3(小問集合)
(1)
階級値×度数の合計を10人で割る。
(0.5×3+1.5×4+2.5×2+3.5×1)÷10
=16÷10
=1.6km
(2)
順番をつけて2枚取り出すから、5P2=5×4=20通り
a≧bとなる場合を数える。
ポイントは2枚ある1を1A、1Bに分けること。
b=1Aのとき、aは1B、2、3、4の4枚。
b=1Bのとき、aは同じく4枚。
b=2のとき、aは3、4の2枚。
b=3のとき、aは4の1枚。
計11通り、確率は11/20
(3)ア
x=-1/3x2において、
x=2のとき、最小値y=-4/3
x=0のとき、最大値y=0
-4/3≦y≦0
イ
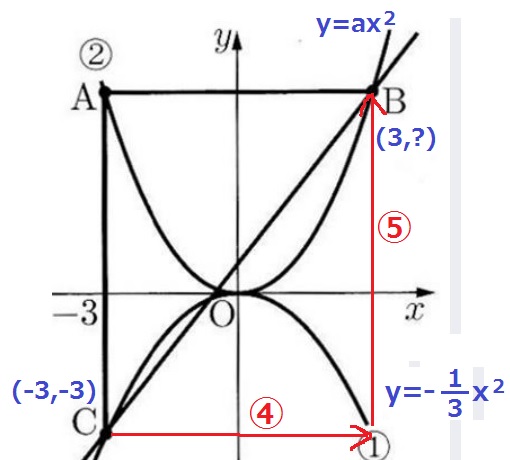
y=-1/3x2にx=-3を代入→C(-3、-3)
ABはx軸に平行なので、A座標とB座標はy軸について対称。
Bのx座標は3
傾きが5/4→右に④すすむと、上に⑤あがる。
A座標とB座標の距離6が④だから、
⑤=6×⑤/④=15/2
Bのy座標は、15/2-3=9/2
y=ax2にC(3、9/2)を代入。
9/2=9a
a=1/2
(4)
答案では求める過程も書く。
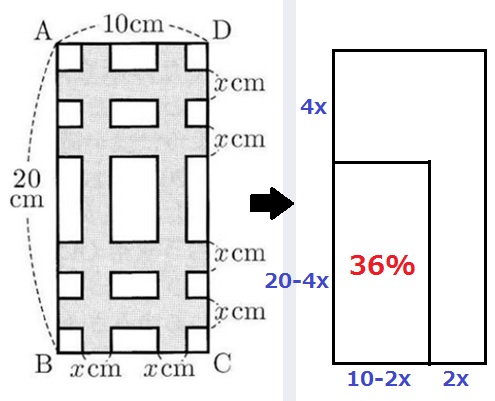
シールなしの場所を端に寄せて長方形にする。
この部分の面積が長方形の36%だから、10×20×36%=72cm2
(20-4x)(10-2x)=72
200-80x+8x2=72
8x2-80x+128=0 ←÷8
x2-10x+16
=(x-2)(x-8)=0
シールが貼られていない部分は残すので、横の長さは2x<10
x<5(xが5cm以上だとすべてにシールが貼られてしまう)
x=2
大問4(整数・方程式)
(1)ア

高さで場合分け。
高さ6→底面は1×1
高さ3→1×2
高さ2→1×3
高さ1→1×6、2×3
以上、5通り
p=5
イ

表中のm=4をみると、n=4、9…
平方数では?
n=16のときを試してみると、
高さ16→底面1×1
高さ8→1×2
高さ4→1×4、2×2
この時点で4通りでてしまうので×!
n=25のとき、
高さ25→底面1×1
高さ5→1×5
高さ1→1×25、5×5
m=4!
25が答えとなる。
@余談@
表を眺めると、nの値が素数のとき、m=2である。
たとえば、n=5のとき、高さは1or5で底面はそれぞれ1つずつしかないからm=2になる。
ここから約数の数がポイントといえる。
n=3(素数)のとき、3の約数は〔1・3〕の2個。
高さ3→1×1、高さ1→1×3でm=2
n=4のとき、4の約数は〔1・2・4〕の3個。
高さ4→1×1、高さ2→1×2、高さ1→1×4、2×2でm=4
高さ1のときだけ2通りで、それ以外は1通りずつで4通りとなる。
ということは、約数が3個のときにm=4になる。
約数が3個→素数×素数、すなわち、素数の平方数である。
(約数が1・素数・それ自身で3個)
n=4=2×2
n=9=3×3
3の次の素数は5、n=25のときm=4となる。
5の次の素数は7、n=49のときm=4となる。
次のnは11の平方数121、その次は13の平方数169、その次は17の平方数289。
(2)ア
条件整理で頭がゴチャりやすい:( ´ω` ):
簡単にまとめる。表を〇、裏を●とすると、
〇〇〇…太郎4点、次郎0点
〇〇●…太郎2点、次郎1点
〇●●…太郎1点、次郎2点
●●●…太郎0点、次郎4点
〇●●だけ3回→太郎3点
他は1回ずつだから、太郎は3+4+2+0=9点
イ
〇〇●が1回。
〇〇〇がa回。
●●●がb回。
〇●●は、10-(1+a+b)=9-a-b回
次郎の点数は0×a+1×1+2(9-a-b)+4b
=-2a+2b+19点
ウ
答案では求める過程も記述する。
問題文がやけに長いが、状況は前問と同じである。
新たに追加された情報は『表の合計が12枚』『次郎は太郎より7点大きい』
1つ目は表の合計で等式。
〇〇〇…a回
〇〇●…1回
〇●●…9-a-b回
●●●…b回
3a+2+(9-a-b)+0=12
2a-b=1 …①
2つ目は点数の合計で等式。
太郎の得点は、4a+2+(9-a-b)+0=3a-b+11点
次郎の得点は、前問より-2a+2b+19点。
3a-b+11+7=-2a+2b+19点
5a-3b=1 …②
①と②の連立を解くとa=2、b=3
大問5(図形の証明)
(1)
△FGH∽△IEHの証明。

頻出のチョウチョウ型ゆえ、ここは絶対とること!
FG//EIの錯角と対頂角で2角が等しく∽
(2)
CE=FGの証明。
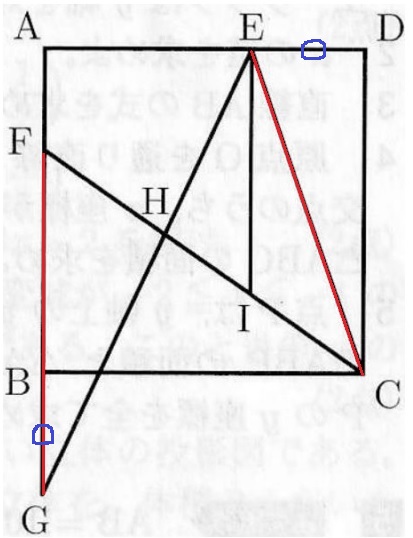
お互いが変な位置関係にある。
FGを1辺とする三角形は△FGHだが、ECを1辺とする三角形とのつながりが見出せない。
こういう一筋縄ではいかない証明問題は、あいだに何かをはさむ場合が多い。
仮定より与えられたDE=BGに着目。
奇妙な等辺を1辺とする三角形をつくる。
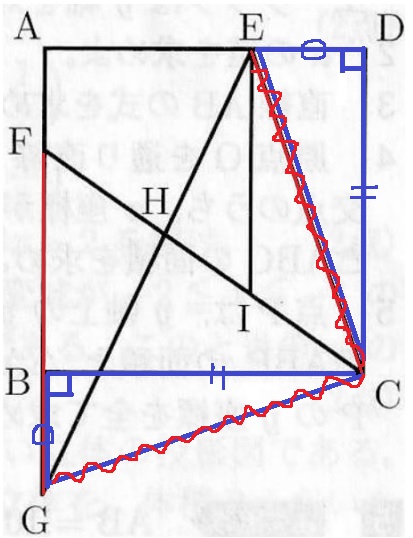
GCに補助線。
DE=BG、DC=BC(正方形1辺)、∠EDC=∠GBC(正方形内角)より、
2辺とあいだの角が等しく、△EDC≡△GBC
対応する辺で、CE=CG
ここからCG=FGにつなげたい…。

まだ使っていない『∠BCEの二等分線』を活用する。
∠FCE=∠FCB(●)
対応する角から、∠ECD=∠GCB(×)
AG//DCより、錯角で∠FCD=∠CFG(●×)
△GFCは2つの底角が等しく、二等辺三角形。
CE=CG=FGとなり、CE=FGがいえる。
●講評●
大問1
ここだけで13点ももらえる。死守。
(5)6に注目してまとめてみる。
大問2
(2)ア:正答はわかりやすい。誤答のチェックに時間をかけすぎないように。
イ:BAの長さがすぐでるので、BP:PAに狙いをしぼる。
BP:PA=△BCP:△PCA。そして立体の体積比へ。
(3)△ABD∽△CEDの5:3を2度活用。
大問3
(2)同じ数字には異なる記号を付して個性を出させる。
(3)イ:Bのx座標は3と早々と確定したい。
(4)範囲に注意!採点ではx<5も見られる。
大問4
(1)ア:高さ1のときに2通りあらわれる。
イ:表から平方数だと察しやすい。
ただし、16ではない!nが素数だとm=2だから、約数の数がポイントである。
16は約数が5個あり、n=8でm=6だから、n=16のときのmはもっと大きくなるはず。
(2)条件整理でイラる。
イウ:問題文がなんか読みにくくて気がめいる。
大問5
(1)死守
(2)直接は求められない。
難易度は易しくないが、与えられた条件が特殊ゆえ方針が思いつきやすい面もある。



コメント